Description
给你两棵二叉树tree1和tree2,检验tree1中是否包含和tree2具有相同结构和结点值的子树。如果存在,输出true;否则,输出false。
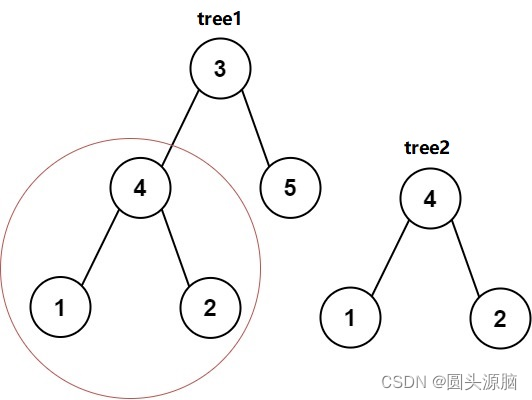
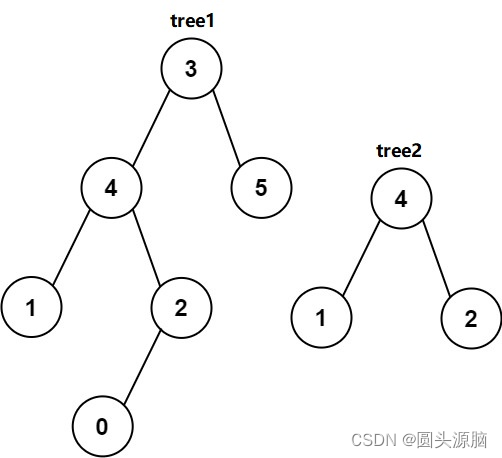
Input
第一行输入t,表示有t个测试样例。
第二行首先输入n1,接着输入n1个整数,表示二叉树tree1。
第三行首先输入n2,接着输入n2个整数,表示二叉树tree2。
以此类推,每两行输入一个测试样例,共输入t个测试样例。
数组形式的二叉树表示方法与题目:DS二叉树_伪层序遍历构建二叉树 相同,输入-1表示空结点。
Output
每一行输出当前测试样例是否符合题意。
共输出t行。

思路分析:
方法一:深度优先搜索暴力匹配



算法实现:
bool SameTree(BitNode* s, BitNode* t) {//如果根节点都为空,匹配成功,返回trueif (s == nullptr && t == nullptr) return true;、//两者之中有一个为空,匹配不成功,返回falseif (s == nullptr || t == nullptr) return false;//三者都相等才是相等的树,必须满足1.根节点值相等; 2.左子树相等 3.右子树相等return s->data == t->data && SameTree(s->lc, t->lc) && SameTree(s->rc, t->rc);
}bool isSubtree(BitNode* s, BitNode* t) {if (!s) return false;//如果 目标树是子树的左子树,或者是右子树,或者两者相等,那么目标树则为主树的子树return isSubtree(s->lc, t) || SameTree(s, t) || isSubtree(s->rc, t);
}
实现代码:
#include<iostream>
#include<queue>
using namespace std;class BitNode {//friend bool isSubtree();//friend bool SameTree();
public:int data;BitNode* lc;BitNode* rc;BitNode() :lc(NULL), rc(NULL) {};BitNode(char e) :data(e), lc(NULL), rc(NULL) {};~BitNode() {delete lc;delete rc;}friend class BinaryTree;
};class BinaryTree {
private:BitNode* root;//头节点void CreateTree(BitNode*& t, int n, int arr[]);int* arr = new int[1000];
public:BinaryTree() :root(NULL) {}~BinaryTree() { delete root; };void CreatTree(int n, int arr[]);BitNode* getRoot() {return root;}
};void BinaryTree::CreateTree(BitNode*& t, int n, int arr[]) {//伪层序遍历构建二叉树t = new BitNode;queue <BitNode*> T;if (arr[0] != -1) {t->data = arr[0];T.push(t);}else {return;}int count = 1;while (count < n && !T.empty()) {BitNode* node = T.front();T.pop();if (arr[count] != -1) {node->lc = new BitNode(arr[count]);T.push(node->lc);}count++;if (count < n && arr[count] != -1) {node->rc = new BitNode(arr[count]);T.push(node->rc);}count++;}
}
void BinaryTree::CreatTree(int n, int arr[]) {CreateTree(root, n, arr);
}bool SameTree(BitNode* s, BitNode* t) {//如果根节点都为空,匹配成功,返回trueif (s == nullptr && t == nullptr) return true; //两者之中有一个为空,匹配不成功,返回falseif (s == nullptr || t == nullptr) return false;//三者都相等才是相等的树,必须满足1.根节点值相等; 2.左子树相等 3.右子树相等return s->data == t->data && SameTree(s->lc, t->lc) && SameTree(s->rc, t->rc);
}bool isSubtree(BitNode* s, BitNode* t) {if (!s) return false;//如果 目标树是子树的左子树,或者是右子树,或者两者相等,那么目标树则为主树的子树return isSubtree(s->lc, t) || SameTree(s, t) || isSubtree(s->rc, t);
//请不要直接复制粘贴
}int main()
{int t;cin >> t;while (t--){int n1;int n2;cin >> n1;int* arr1 = new int[n1 + 1];for (int i = 0; i < n1; i++) {cin >> arr1[i];}cin >> n2;int* arr2 = new int[n2 + 1];for (int i = 0; i < n2; i++) {cin >> arr2[i];}BinaryTree* tree1 = new BinaryTree;tree1->CreatTree(n1, arr1);BinaryTree* tree2 = new BinaryTree;tree2->CreatTree(n2, arr2);if (isSubtree(tree1->getRoot(), tree2->getRoot())) {cout << "true" << endl;}else {cout << "false" << endl;};}
}