Learning Search Space Partition for Black-box Optimization using Monte Carlo Tree Search
目标:从采样(Dt ∩ ΩA)中学习一个边界,从而最大化两方的差异
先使用Kmeans在特征向量上( [x, f(x)] )聚类,然后使用SVM划分出边界
通过learning+splitting构建一个树 --> 根据UCB选择一个区域 --> 在选择的区域上,进行采样
一、通过splitting进行动态树的构建
“Dynamic tree construction via splitting”这一段描述了一种动态树结构的构建方法,该方法通过分割操作来实现。具体来说,这个过程涉及以下几个步骤:
1、性能估计:通过计算在某个区域Ωi内所有样本xi的函数值f(xi)的平均值来估计该区域的性能,其中ni是该区域内样本的数量,xi ∈ Dt ∩ Ωi是在迭代t时收集的样本。
![]()
2、迭代收集新样本:在每次迭代中,收集新的样本xi,并且对于这些新样本,区域的性能估计误差|ˆv∗ni − v∗ni|会迅速减小。当这个误差达到一个平稳状态时,意味着不需要再收集新的样本。
3、使用潜在动作分割:一旦性能估计误差达到稳定,LA-MCTS会使用潜在动作来分割当前区域,从而继续精细化两个子区域的价值估计。潜在动作是指通过支持向量机(SVM)学习到的边界,它将节点代表的区域分割成高性能和低性能的两个区域。
4、树的深化:随着越来越多的样本从有希望的区域收集,树会向更好的区域深入,从而更好地引导搜索过程朝向最优解。
5、分割阈值θ:在实践中,使用一个阈值θ作为可调参数来控制分割。如果在任何叶子节点上,Dt ∩ Ωi的大小超过了阈值θ,就会对该叶子节点进行分割。
这个动态树构建过程的目的是为了更好地引导贝叶斯优化(BO)算法,特别是在高维问题中,通过直接在Ωleaves上优化来帮助BO算法避免过度探索,从而提高性能。
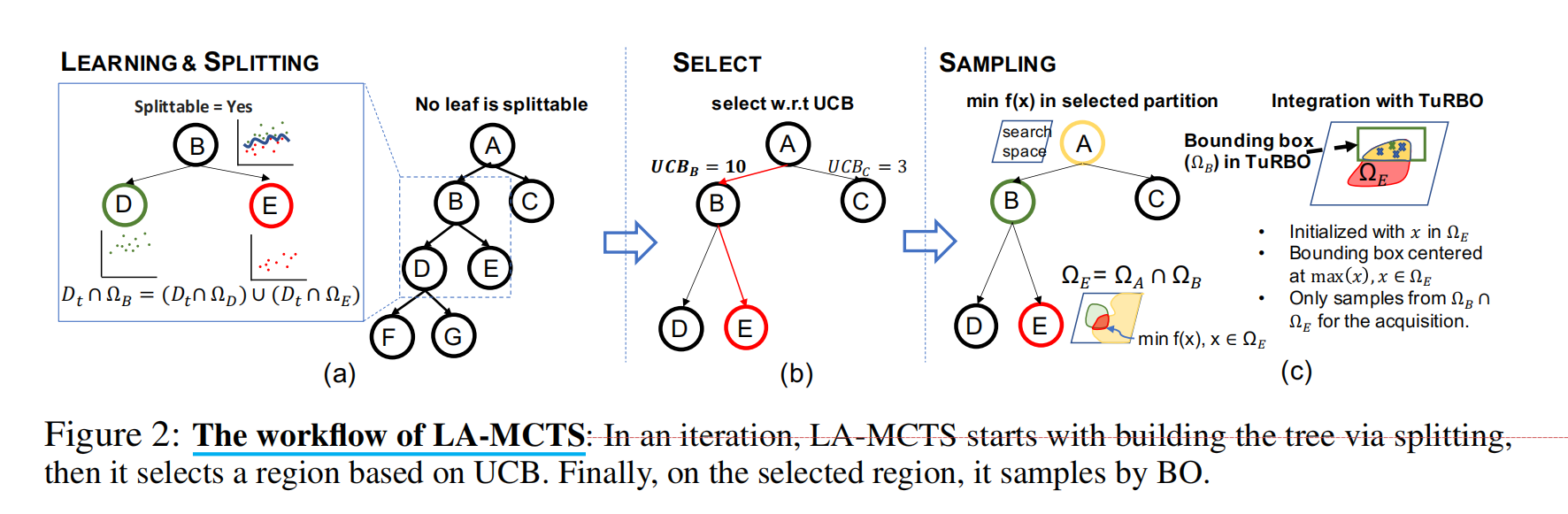
我们的搜索树的结构在迭代过程中动态变化,这与LaNAS中使用的预定义固定高度树不同。在迭代开始时,从包含所有样本的根开始,如果任何叶子的样本量超过分裂阈值θ,我们使用潜在动作递归地分裂叶子,例如在图2(a)中为节点B创建节点D和节点E。我们停止树的分裂,直到没有更多的叶子满足分裂标准。然后,树就可以在这个迭代中使用了。
二、通过UCB选择节点
本文使用UCB选择节点而不是贪心算法,因为UCB可以建立对整个搜索空间的全局视图。UCB的定义为每个节点的UCB如下,其中vj是节点j的平均值,nj是节点j的访问次数,np是节点j的父节点的访问次数,Cp是一个可调节的超参数,用于控制探索的程度。
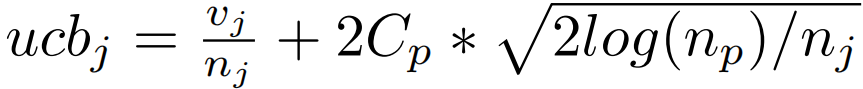
通过从根节点到叶节点的路径选择一个分区进行采样,这个路径上的支持向量机(SVM)共同定义了一个用于采样的区域。例如,在图2(c)中,选择的区域为ΩE。在采样过程中,LA-MCTS在这个受限的搜索空间Ωselected上解决最小化目标函数f(x)的问题。
整个过程的目的是在保持对最有前途区域的关注的同时,确保算法不会过度探索或者忽视潜在的好区域。Cp参数的选择对算法的性能有显著影响,过小的Cp会导致性能下降,因为它可能忽略了探索;而过大的Cp则可能导致过度探索。文档建议将Cp设置为最大目标函数值的10%到1%。
三、通过贝叶斯优化BO进行采样
在文档中,“Sampling via Bayesian Optimizations”这一部分讲述了如何在贝叶斯优化(Bayesian Optimization, BO)框架内进行采样。它描述了在蒙特卡洛树搜索(LA-MCTS)中如何通过选择一条从根到叶的路径来确定一个采样区域。这个区域由路径上的支持向量机(SVM)共同定义,并且在这个区域内进行最小化目标函数f(x)的求解。
在与TuRBO(Truncated Robust Bayesian Optimization)集成的过程中,文档提到了几个关键的调整点:
-
在每次TuRBO重启时,只在选定的区域(Ωselected)内用随机样本进行初始化。由于选定区域的形状可能是任意的,因此使用拒绝采样(均匀采样并用SVM拒绝异常值)来获得Ωselected内的一些点。由于只需要少量样本进行初始化,所以拒绝采样就足够了。
-
TuRBO将一个边界框(bounding box)定位在到目前为止最好的解决方案上,而在LA-MCTS中,中心被限制在Ωselected中的最佳解决方案上。
-
TuRBO从边界框中均匀采样以选择下一个样本,而在LA-MCTS中,TuRBO被限制在边界框与Ωselected的交集中均匀采样。由于中心在Ωselected内,所以交集的存在是有保证的。
在每次迭代中,TuRBO会一直运行,直到信任区域(trust-region)的大小变为0,并且所有评估(例如xi和f(xi))都返回给LA-MCTS,以便在下一次迭代中细化学习到的边界。
这一部分的重点是在高维空间中,特别是在采样区域受限的情况下,如何有效地进行采样。文档提到了一些替代的采样方法,如hit-and-run或Gibbs采样,这些方法可能是拒绝采样的好替代品,因为在高维空间中,拒绝采样可能无法在Ωselected中获得足够的随机样本。文档还提出了一种新的启发式采样方法,即在Ωselected内的每个现有样本x处,绘制一个超立方体,并扩展这个立方体同时拒绝异常值。
Sampling with TuRBO:
here we illustrate the integration of SoTA BO method TuRBO [2] with LA-MCTS. We use TuRBO-1 (no bandit) for solving minf(x) within the selected region, and make the following changes inside TuRBO, which is summarized in Fig. 2(c).
a) At every re-starts, we initialize TuRBO with random samples only in Ωselected. The shape of Ωselected can be arbitrary,so we use the rejected sampling (uniformly samples and reject outliers with SVM) to get a few points inside Ωselected. Since we only need a few samples for the initialization, the reject sampling is sufficient.
b) TuRBO centers a bounding box at the best solution so far, while we restrict the center to be the best solution in Ωselected.
c) TuRBO uniformly samples from the bounding box to feed the acquisition to select the best as the next sample, and we restrict the TuRBO to uniformly sample from the intersection of the bounding box and Ωselected. The intersection is guaranteed to exist because the center is within Ωselected. At each iteration, we keep TuRBO running until the
size of trust-region goes 0, and all the evaluations, i.e. xi and f(xi), are returned to LA-MCTS to
refine learned boundaries in the next iteration. Noted our method is also extensible to other solvers
by following similar procedures.








](https://img-blog.csdnimg.cn/6d064cc98cb7481f8dd77a0c85b2fb20.png)