17. 机器学习 - 随机森林

茶桁的AI秘籍核心基础 17

Hi，你好。我是茶桁。

我们之前那一节课讲了决策树，说了决策树的优点，也说了其缺点。

决策树实现起来比较简单，解释解释性也比较强。但是它唯一的问题就是不能拟合比较复杂的关系。

后来人们为了解决这个问题，让其能够拟合更加复杂的情况，提出来了一种模型，这种模型就叫做随机森林。

随机森林

随机森林之所以叫随机森林，是因为它是由多棵树组成。它结合了决策树和随机性的概念，用于解决分类和回归问题，随机森林由多个决策树组成，每棵树都是随机构建的。

随机森林其核心组成部分是决策树，为了提高模型的性能和泛化能力，所以引入了两种主要形式的随机性。

第一种就是随机选择样本，对于每棵决策树的构建，随机森林从训练数据中随机抽取一部分样本（有放回地抽样），这称为自助采样（Bootstrap Sampling）。这就使得每棵树都在不同的样本子集上进行训练，增加了模型的多样性。

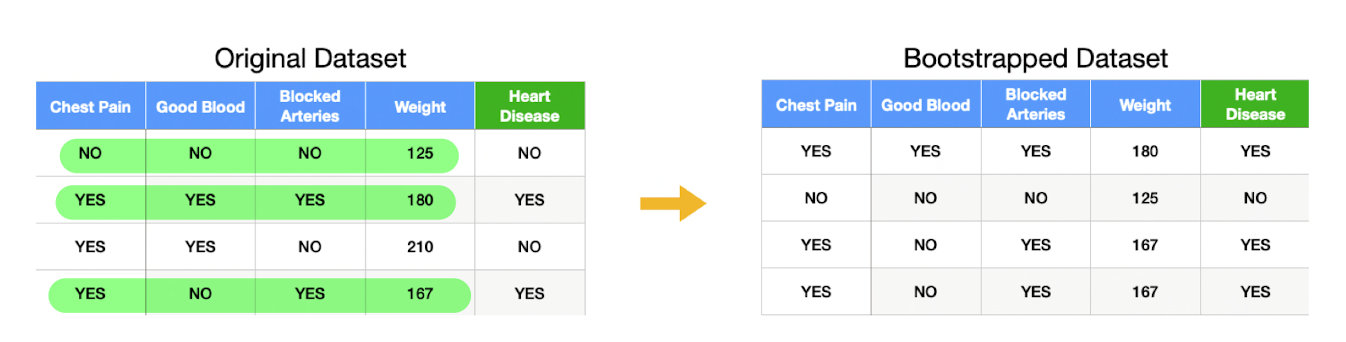
Alt text

第二种是随机选择特征，在每个节点上，随机森林只考虑特征的一个子集来进行分割决策，而不是考虑所有特征。这确保了每棵树的分裂过程是不同的，增加了多样性。

对于分类问题，随机森林中的每棵决策树都会对输入数据进行分类，那对于回归问题，就会变成是每棵决策树都会对输入数据进行预测了。最后的预测结果是通过对所有树的投票或平均值来获得的。这种集成方法可以减小过拟合奉先，提高模型的稳定性和泛化能力。

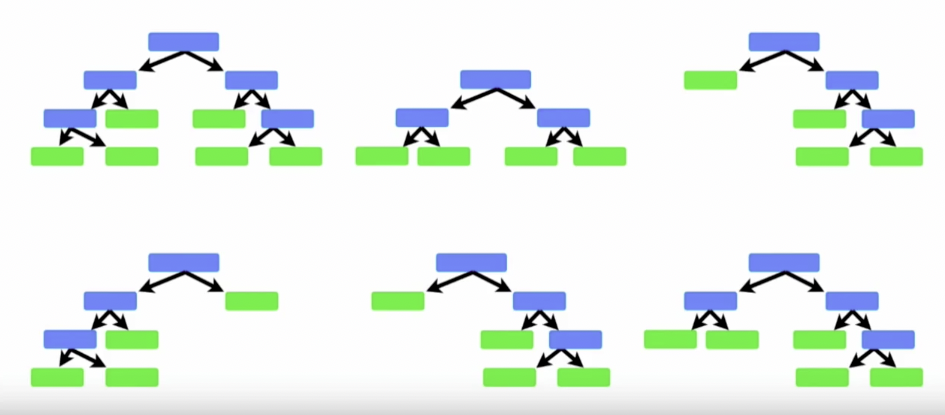
Alt text

使用随机森林来预测。
在预测之前呢，我们使用 Out-Of-Bagging 样本来评估我们的模型。这个bagging就是袋子，就是我们从袋子里随机取东西去衡量。
使用评估结果，我们可以选择合适的变量数。

随机森林的原理其实很简单，是一个非常简单但是非常好用的一个方法。基本上，除了深度学习之外，也是企业用的最多的方法之一。咱们在这里就来演示一下随机森林的作用以及效果：

from sklearn.datasets import load_iris
iris = load_iris()x = iris.data
y = iris.target
print(x, y)

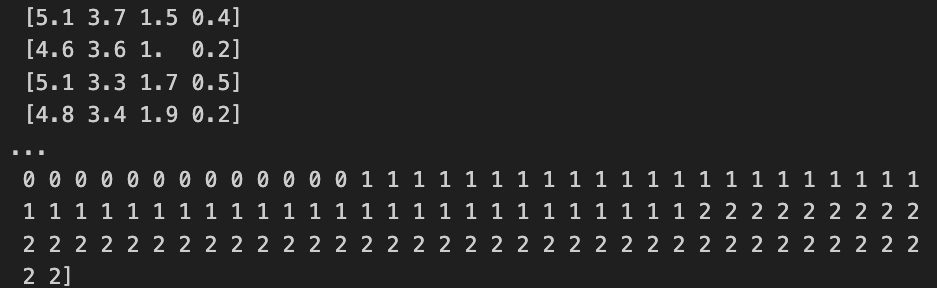
Alt text

这个是我们用sklearn里面鸢尾花分类的数据做个简单例子，快速的展现一下它的效果。我们将数据拿到以后，x是鸢尾花的四个维度，四个维度对应了它的一个类别。

from sklearn.tree import DecisionTreeClassifiertree_clf = DecisionTreeClassifier()
tree_clf.fit(x, y)tree_clf.feature_importances_---
array([0.02666667, 0.        , 0.05072262, 0.92261071])

我们fit完之后就可以看到，这四个feature中，最终要的是第四个feature。然后是第三个，第二个根本就没用。

from sklearn.model_selection import train_test_splittrain_x, test_x,train_y, test_y = train_test_split(x, y, test_size=0.3, random_state=0)tree_clf = DecisionTreeClassifier()
tree_clf.fit(train_x, train_y)print(tree_clf.score(train_x, train_y))
print(tree_clf.score(test_x, test_y))---
1.0
0.9777777777777777

看结果我们其实可以看到，这个拟合度有点太高了。我们换个数据再来看, 还是之前的课程中我们用到的Boston房价的数据，不过因为这个是一个回归问题，所以我们需要用回归预测的方法：

from sklearn.tree import DecisionTreeRegressor
from sklearn.datasets import fetch_openml
dataset = fetch_openml(name='boston', version=1, as_frame=True, return_X_y=False, parser='pandas')data = dataset['data']
target = dataset['target']x_train, x_test, y_train, y_test = train_test_split(data, target, test_size=0.2)tree_reg = DecisionTreeRegressor()
tree_reg.fit(x_train, y_train)print('whole dataset train acc: {}'.format(tree_reg.score(x_train, y_train)))
print('whole dataset test acc: {}'.format(tree_reg.score(x_test, y_test)))---
whole dataset train acc: 1.0
whole dataset test acc: 0.6606392933985246

现在我们来看，它的train上的score准确度是1.0，在test上是0.81，这个是全数据量测试的情况。

然后我们来定义一个函数：

def random_forest(x_train, y_train, x_test, y_test, drop_n=4):features_random = np.random.choice(list(x_train.columns), size=len(x_train.columns)-drop_n)x_sample = x_train[features_random]y_sample = y_trainreg = DecisionTreeRegressor()reg.fit(x_sample, y_sample)score_train = reg.score(x_sample, y_sample)score_test = reg.score(x_test[features_random], y_test)print('sub sample :: train score: {}, test score: {}'.format(score_train, score_test))y_predicated = reg.predict(x_test[features_random])return y_predicated

咱们随机的从data里面取一些数据，之后我们来看一下单个树的结果：

with_feature_names = pd.DataFrame(data)
with_feature_names.columns = dataset['feature_names']x_train, x_test, y_train, y_test = train_test_split(with_feature_names, target, test_size=0.3, random_state=0)random_forest(x_train, y_train, x_test, y_test, 4)---
sub sample :: train score: 1.0, test score: 0.5171643497313849

单个的结果显然是要比整个的数据量要差。那么咱们现在看一下最终的结果,把它变成一个森林：

tree_num = 4
predicates = []
for _ in range(tree_num):predicated, score = random_forest(x_train, y_train, x_test, y_test)predicates.append((predicated))print('the mean result is: {}'.format(np.mean(predicates), axis=0))
print('the score of forest is: {}'.format(r2_score(y_test, np.mean(predicates, axis=0))))---
the mean result is: 21.614144736842107
the score of forest is: 0.7194989474162439

从一开始到现在完整的打印结果为：

whole dataset train acc: 1.0
whole dataset test acc: 0.6606392933985246ssub sample :: train score: 1.0, test score: 0.5885292814825753
sub sample :: train score: 1.0, test score: 0.559086368163823
sub sample :: train score: 1.0, test score: 0.6119989116140754
sub sample :: train score: 1.0, test score: 0.21831688326567122the mean result is: 21.614144736842107
the score of forest is: 0.7194989474162439

这是个很典型的例子，使用全量的数据集，它的结果最终的在test集上是0.66，然后基本上每个的结都比它要差一些。但当我们用了森林的值做了平均之后，这个值就变得更好了。

当然其实这个值并不是每次都是如此，在我们进行计算的时候，因为数据什么的都是随机的，偶尔也会出现取均值之后变的更差的情况。不过大部分时候，都会更好一些。

我们现在再将结果稍微改一改：

def random_forest(x_train, y_train, x_test, y_test, drop_n=4):...return y_predicated, score_testtree_num = 4
predicates = []
for _ in range(tree_num):predicated, score = random_forest(x_train, y_train, x_test, y_test)predicates.append((predicated, score))predicates_value = [v for v, s in predicates]
forest_scores = [s for v, s in predicates]print('the score of forest is: {}'.format(r2_score(y_test, np.mean(predicates_value, axis=0))))weights = np.array(forest_scores) / np.sum(forest_scores)
score_weights = np.zeros_like(np.mean(predicates_value, axis=0))for i, v in enumerate(predicates_value):score_weights += v * weights[i]print('the score of weighted forest is: {}'.format(r2_score(y_test, score_weights)))---
the score of forest is: 0.7049603534192553
the score of weighted forest is: 0.7204901503020483

后面这段代码呢，其实就是人们发现用了随机森林之后，效果明显要好了，那一些人就想如果在知道每一次的test_score之后，能不能给test_score比较高的值加一个比较大的权重。

也就是说，当我知道test_score比较好，那在最后做决策的时候给它加的权重大一些。

最后我们打印了常规状态下森林的结果和加权之后的结果。加权之后的结果又变得好了一些。

Adaboost

然后人们沿着这个思路，就做了一件事情，就是Adaboost(Adaptive Boosting)：

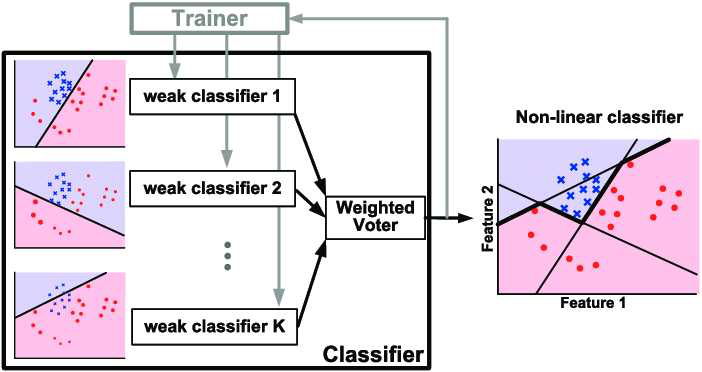
Alt text

Adaboost就是在随机森林的权重思路上做了一个优化，它的示意图也是有多个weak classifier, 然后最后有一个Weighted Voter, 这是一个权重的投票，这个就和我们上面加权的那部分代码非常的类似。只不过它在这里做了个细化：

Alt text

我们来注意看最后一个公式：

$sign(\sum_{t=1}^T\alpha_th_t(x))$

公式里的 $\alpha_t$ 就是它的权重，最终的H(x)就是很多 $\alpha_t \cdot h_t(x)$ 加在一起的结果。这里的这个 $\alpha_t$ 就是每一次小的数的权重：v * weights[i]。这个权重就不是像咱们刚才代码里那样根据score的大小简单的做个加权。

我们看上图中间又一个 $\alpha_t$ 的公式:

$\begin{align*} \alpha_t = \frac{1}{2}ln(\frac{1-\varepsilon_t}{\varepsilon_t}) \end{align*}$

然后我们再往上倒腾， $\varepsilon_t$ 是当你预测出来这个值和实际值错的越多, 越趋近于1。如果完全没有错，一个错都没有的情况下，那么 $\varepsilon_t=0$ 。

$\begin{align*} \varepsilon_t = Pr_{i\sim D_t}[h_t(x_i)\ne y_i] \end{align*}$

如果 $\varepsilon_t = 1$ 的话, 那就是 $\frac{1-\varepsilon_t}{\varepsilon_t}$ 就是：1-1/1=0。ln0等于什么呢？它等于负的无穷大，那么 $\alpha_t$ 等于就没有。如果 $\varepsilon_t = 0$ ， $ln(\frac{1-\varepsilon_t}{\varepsilon_t})$ 就是无穷大。

也就是说,随着 $\varepsilon_t$ 越大, 那 $\alpha_t$ 会越大，随着 $\varepsilon_t$ 越小, $\alpha_t$ 也会越小。而且在这个地方是呈指数变化的，就是误差会对 $\alpha_t$ 的变化影响的很大。

除了用指数的东西来做，它还有一个很重要的特性, 这个特性才在我们整个Adaboost里非常重要：

$D_{t+1}(i) = \frac{D_t(i)exp(-\alpha_ty_ih_t(x_i))}{Z_t}$

我们先来看 $y_ih_t(x_i)$ 这部分，假设ht(xi)=1， yi预测对了等于1， yi预测错了等于-1。那如果预测错了，这整个部分都等于-1，如果预测对了，这里就是1。

前面有一个负号： $-\alpha_ty_ih_t(x_i)$ ，那肯定是要变号的。也就是说，如果预测错了，那么这一串东西应该是正的，如果预测对了这一串东西应该是负的。

前面是什么，是 $D_{t+1}(i)$ , 这里其实就是第i个训练元素在 $D_{t+1}$ 被取到的概率。那么我们最前面有表示 $D_1(i) = \frac{1}{m}$ ，也就是说，所有元素被取到的概率都是一样的，是平均的。那第二次的概率就是: $D_1(i)\cdot exp(...)$ , exp就是e的多少次方。

那我们现在知道，如果预测对了，这里是-1，预测错了这里是1, 都要再乘以 $\alpha_t$ 。那么如果预测对了，这里是 $-\alpha_t$ ，那exp这里就是小于1的。那如果预测错了呢，exp就是大于1的。

如果exp大于1，那么 $D_{t+1}(i)$ 概率就会被 $D_t(i)$ 的概率要更大，反之就会更小。

这个就是我们Ada的含义，Ada就是Adaptive，就是动态调整的意思。也就是通过这种方法实现的。

如果此时此刻 $x_i$ 算对了，那下一次就更不容易被取到，如果算错了，那下一次训练就会更有可能被取到。

觉得绕的小伙伴去理解这样一个例子：如果你是个学生去做卷子，那么你作对的题还会反复去做吗？肯定是不会的题才会反复刷，刷到自己会为止。

Gradient Boosting

除了Adaboost之外，后来人们又提出来了一个新的方法： Gradient Boosting。

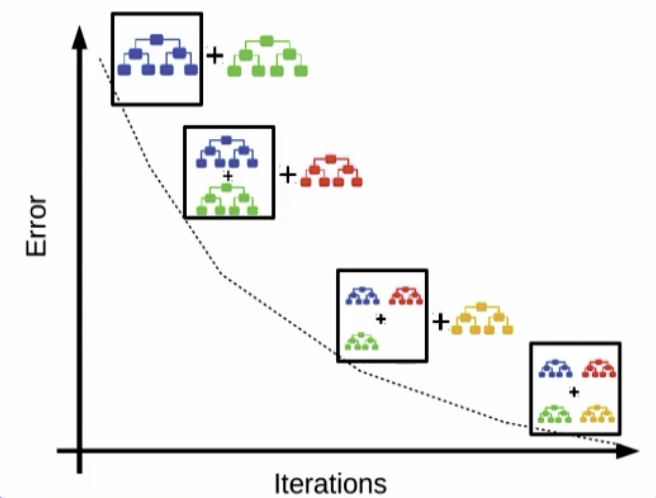
Alt text

Gradient Boosting和Adaboost的核心原理很像:

$-\sum_{i\in output classes}p(x)logq(x)$

Gradient Boosting主要用于解决回归和分类问题。它基于决策树（通常是浅层决策树）构建模型，通过迭代改进预测的准确性。

其最核心的就是梯度提升，是一种集成学习方法。将多个弱预测模型，也就是决策树组合在一起，以提高整体性能。每个决策树在不同的数据子集上训练，然后进行组合以生成最终的预测。其核心原理就是通过迭代优化损失函数来构建模型。

在每一步中，模型的更新方向就是损失函数的负梯度。假设我们有一个损失函数L(y, f(x))，其中y是真实标签, f(x)是当前模型的预测，梯度提升的目标是找到一个新的模型h(x), 使得损失函数L(y, f(x) + h(x))最小化。

梯度提升使用负梯度方向的决策树h(x)来拟合当前模型的残差，因此可以通过以下方式迭代更新模型：

$learning\_rate \cdot h(x) \\$

也就是说，它其实要变成这样一个式子：

$\eta \cdot Second Tree \\ loss(Boosted Ensemble) < loss(First Tree)$

也就是说，我们第二波的h_t(x)，也就是h_2(x)，前面乘以一个 $\eta$ ，这个 $\eta$ 是等于Learning Rate的，然后h_2(x)加上h_1(x)最后得到的结果，要比h_1(x)的loss值更小。

Alt text

那么我们现在要做的就是改变 $\eta$ 的权重，这个东西的权重就是和之前我们在随机森林里调整权重不同。

一开始，梯度提升初始化一个简单的模型，通常是一个常数，用来拟合目标变量的平均值。

对于每一个训练样本，计算模型的梯度。这表示模型对于每个样本的预测误差。

使用新的决策树来拟合梯度的负梯度，也就是模型的残差。这意味着构建一个决策树，其目标是减小之前模型的误差。

将新构建的决策树与之前的模型相加，以形成一个新的模型。这个过程重复进行多次，每次都会减小误差。

重复2到4步，直到满足某个停止条件，理入达到最大迭代次数或误差足够小。

最终模型是所有决策树的组合，可以用来进行预测。

那我们之前谈到的 $\eta$ ，也就是learning_rate，其实就是学习率，用于控制每次更新的幅度。

数学上，梯度提升通过迭代不断减小损失函数来逼近最优模型，这是一种梯度下降的优化方法，因此它的核心原理与梯度下降算法是密切相关的。

Grading Boost和AdaBoost的整个区别不大，它们都是属于Ensemble Learning，中文翻译是合唱团。

这个Ensemble Learning我们可以取很多个分类、回归，然后我们把它做好之后给它求一个平均值。

Alt text

比如这样，

from sklearn.ensemble import RandomForestClassifier
from sklearn.ensemble import VotingClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.svm import SVClog_clf = LogisticRegression()
rnd_clf = RandomForestClassifier()
svm_clf = SVC()voting_clf = VotingClassifier(estimators = [('lr', log_clf),('rf', rnd_clf),('svc', svm_clf)], voting='hard')voting_clf.fit(x_train, y_train)
...