所有的LeetCode题解索引，可以看这篇文章——【算法和数据结构】LeetCode题解。

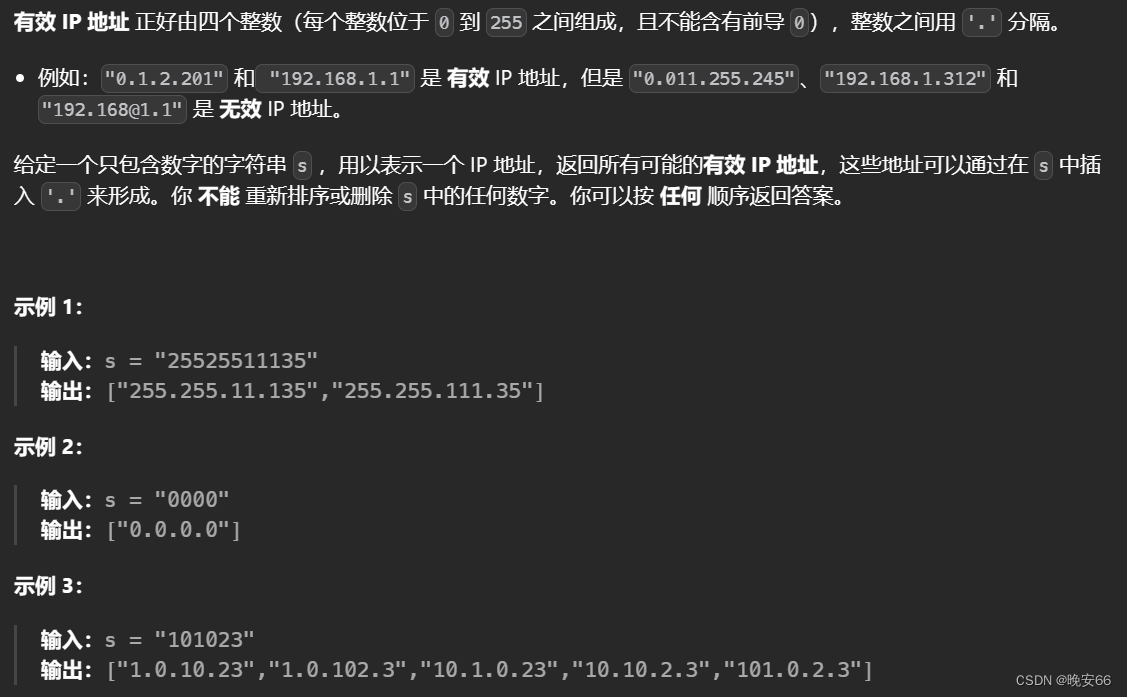
一、题目

二、解法

  思路分析：参照【算法与数据结构】131、LeetCode分割回文串的思路，需要将IP字符串进行分割，同时要对分割字符串的合法性进行判断。IP字符串一共有四个子串，前三个子串在for循环中找到，最后咋终止条件中判断第四个子串是否合法，如果合法则加入结果数组。
  程序如下：

class Solution {
private:vector<string> result;int PointNum = 0;bool isValid(const string& s, int start, int end) {if (start > end) return false;	// start>end的数字不合法if (s[start] == '0' && start!=end) return false;	// 0开头的数字不合法		int num = 0;for (int i = start; i <= end; i++) {if (s[i] < '0' || s[i]>'9') return false;num = num * 10 + (s[i] - '0');if (num > 255) return false;}return true;}void backtracking(string& s, int startIndex) {if (PointNum == 3) {if(isValid(s, startIndex, s.size()-1)) result.push_back(s);	// 判断最后一个子串是否合法，如果合法直接加入结果数组	return;}for (int i = startIndex; i < s.size(); i++) { if (isValid(s, startIndex, i)) {	// 判断子串是否合法s.insert(s.begin() + i + 1, '.');	// 插入分隔符PointNum++;backtracking(s, i + 2);			// 递归PointNum--;s.erase(s.begin() + i + 1);	// 回溯}else break;			}}
public:vector<string> restoreIpAddresses(string s) {backtracking(s, 0);return result;}
};

复杂度分析：

• 时间复杂度： $O(3^4)$， IP地址一共包含四个子串，相当于递归的深度，每个子串有三种分割方式，因此最终时间复杂度为$O(3^4)$。
• 空间复杂度：$O(n)$。

三、完整代码

# include <iostream>
# include <string>
# include <vector>
using namespace std;class Solution {
private:vector<string> result;int PointNum = 0;bool isValid(const string& s, int start, int end) {if (start > end) return false;	// start>end的数字不合法if (s[start] == '0' && start!=end) return false;	// 0开头的数字不合法		int num = 0;for (int i = start; i <= end; i++) {if (s[i] < '0' || s[i]>'9') return false;num = num * 10 + (s[i] - '0');if (num > 255) return false;}return true;}void backtracking(string& s, int startIndex) {if (PointNum == 3) {if(isValid(s, startIndex, s.size()-1)) result.push_back(s);	// 判断最后一个子串是否合法，如果合法直接加入结果数组	return;}for (int i = startIndex; i < s.size(); i++) { if (isValid(s, startIndex, i)) {	// 判断子串是否合法s.insert(s.begin() + i + 1, '.');	// 插入分隔符PointNum++;backtracking(s, i + 2);			// 递归PointNum--;s.erase(s.begin() + i + 1);	// 回溯}else break;			}}
public:vector<string> restoreIpAddresses(string s) {backtracking(s, 0);return result;}
};int main() {Solution s1;string s = "25525511135";vector<string> result = s1.restoreIpAddresses(s);for (vector<string>::iterator jt = result.begin(); jt != result.end(); jt++) {cout << *jt << endl;}cout << endl;system("pause");return 0;
}

end