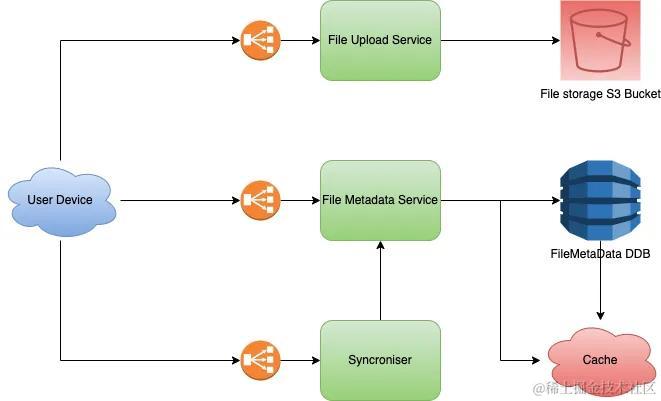
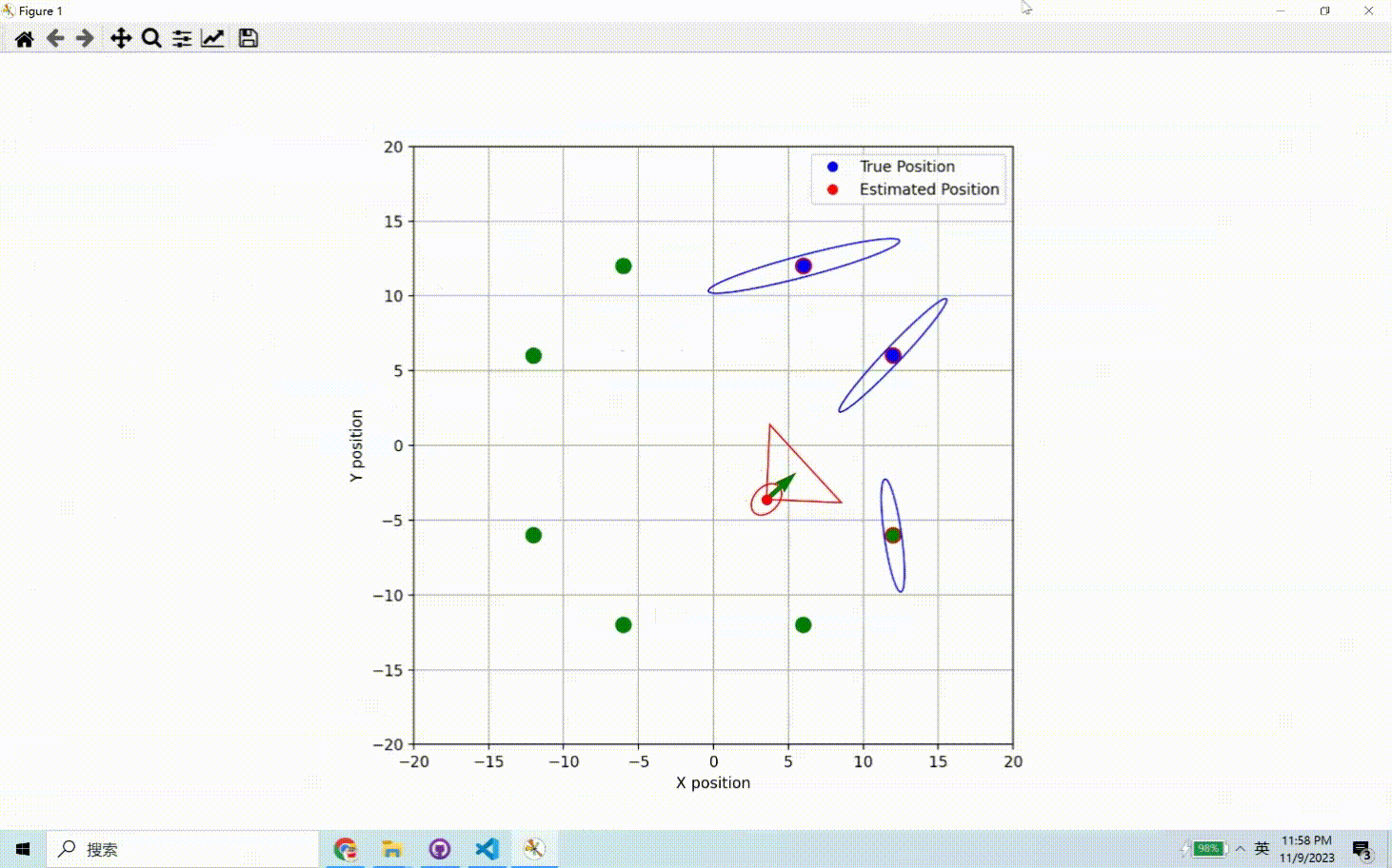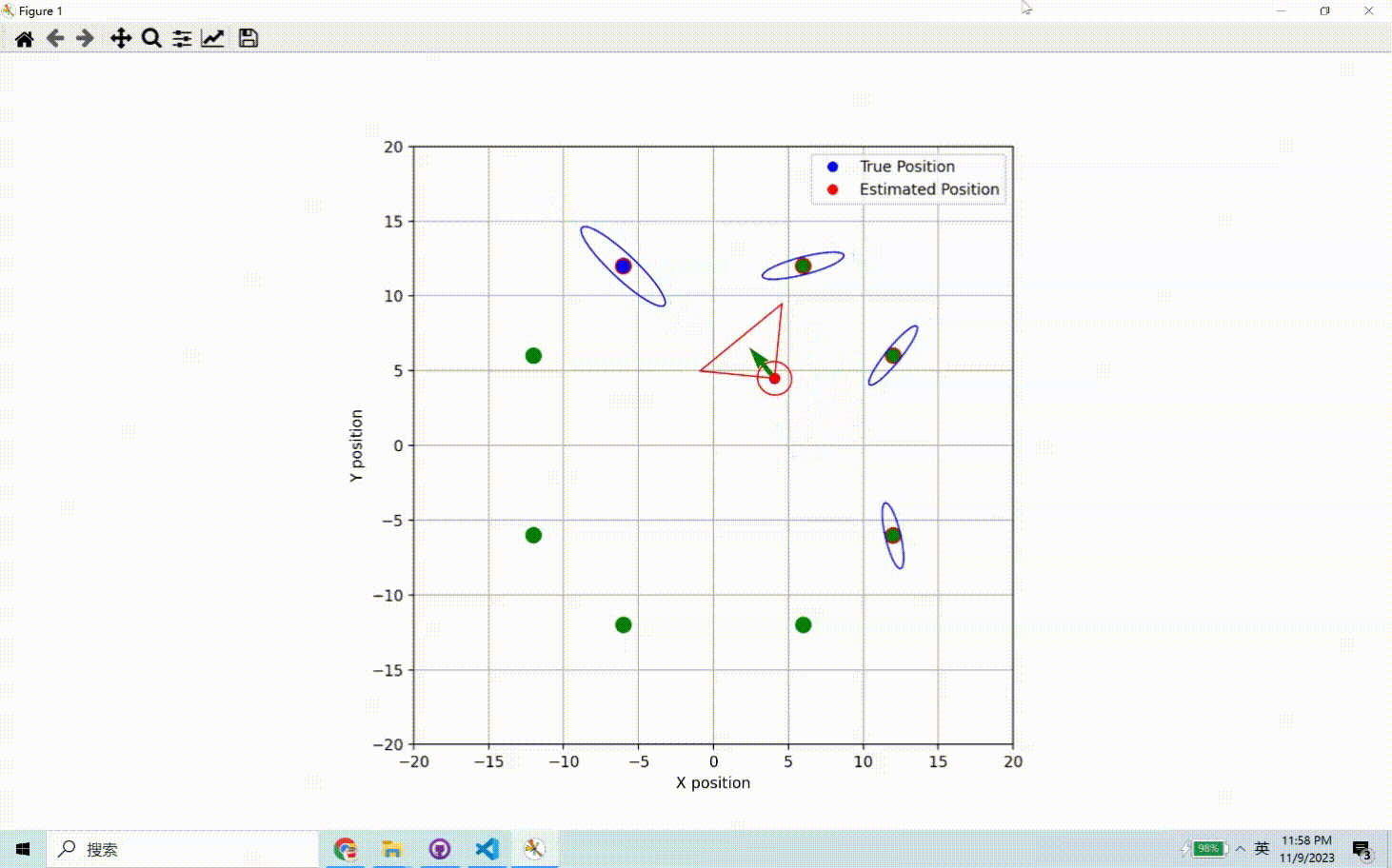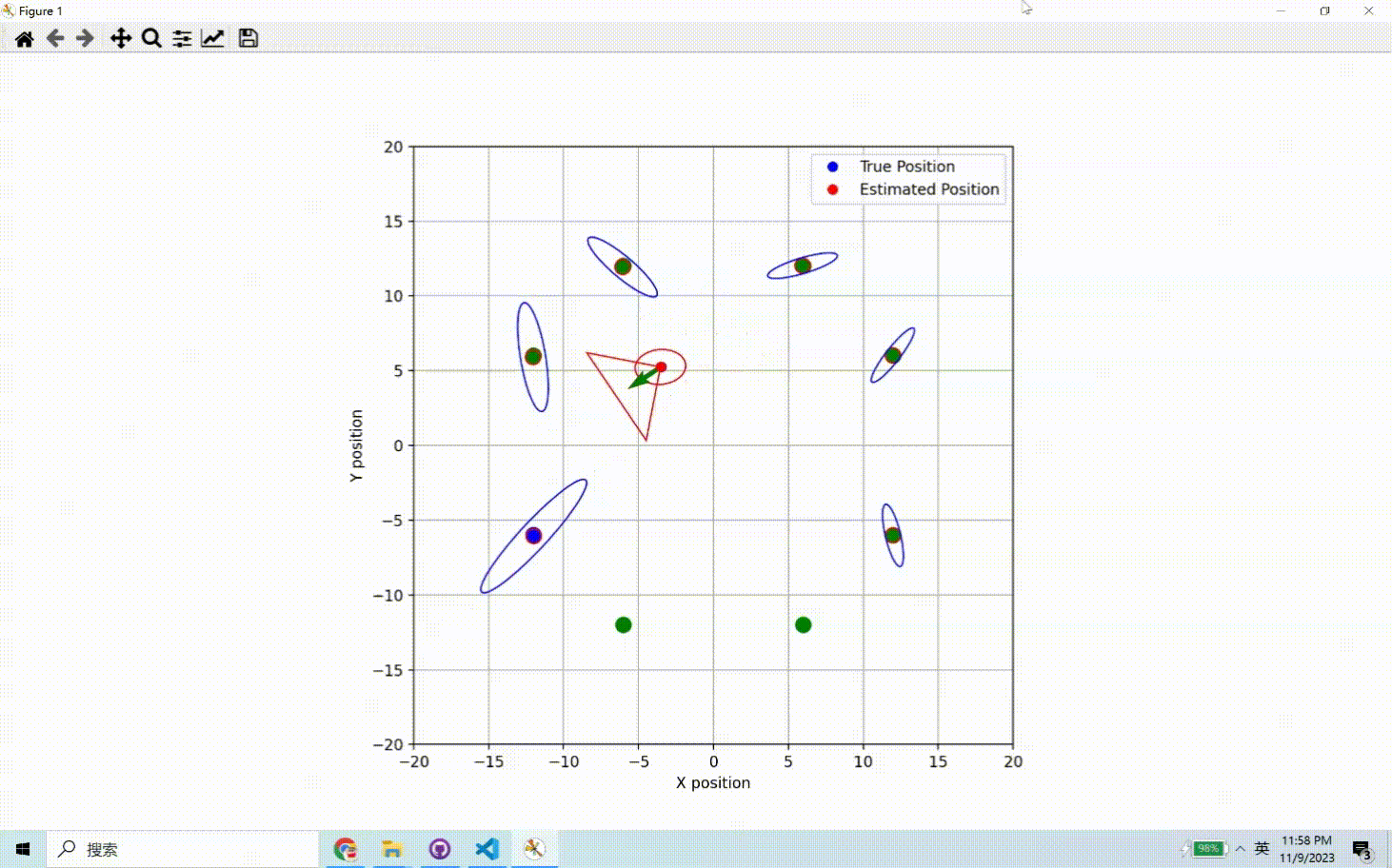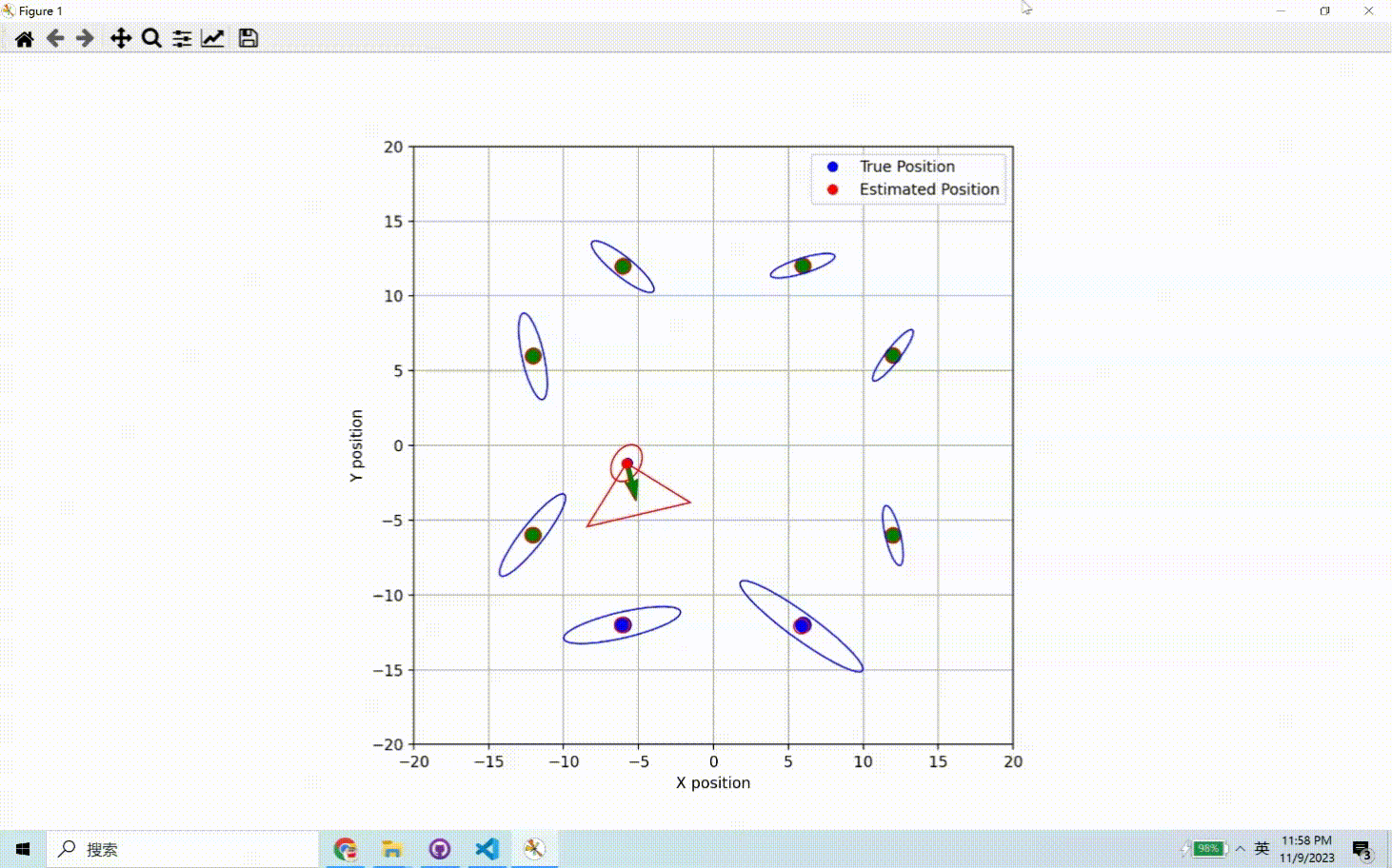
代码地址及效果

代码地址

运动预测

简化控制量 $u_t$ 分别定义为 $v_x\Delta t$，$v_y\Delta t$，和 ${\omega }_z\Delta t$。这样，我们将离散时间控制向量 $u_k$ 表示为：
$$u_k=\left[\begin{array}{c}\Delta {\mu }_1\\ \Delta {\mu }_2\\ \Delta \theta \end{array}\right]=\left[\begin{array}{c}{v}_x\Delta t\\ v_y\Delta t\\ {\omega }_z\Delta t\end{array}\right]$$

这里，$\Delta {\mu }_1$ 和 $\Delta {\mu }_2$ 表示在 $\Delta t$ 时间内沿X和Y轴的速度增量，而 $\Delta \theta$ 是在 $\Delta t$ 时间内绕Z轴的角速度增量。状态更新方程如下：

$${\left[\begin{array}{c}x\\ y\\ \theta \end{array}\right]}_{t|t-1}={\left[\begin{array}{c}x\\ y\\ \theta \end{array}\right]}_{t-1}+\left[\begin{array}{ccc}\cos ({\theta }_{t-1})& -\sin ({\theta }_{t-1})& 0\\ \sin ({\theta }_{t-1})& \cos ({\theta }_{t-1})& 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}\Delta {\mu }_1\\ \Delta {\mu }_2\\ \Delta \theta \end{array}\right]$$

简化上述方程得到：

$${\left[\begin{array}{c}x\\ y\\ \theta \end{array}\right]}_{t|t-1}=\left[\begin{array}{c}{x}_{t-1}+\Delta {\mu }_1\cos ({\theta }_{t-1})-\Delta {\mu }_2\sin ({\theta }_{t-1})\\ y_{t-1}+{\mu }_1\sin ({\theta }_{t-1})+{\mu }_2\cos ({\theta }_{t-1})\\ {\theta }_{t-1}+\Delta \theta \end{array}\right]$$

考虑到 $\Delta {\mu }_1$ 和 $\Delta {\mu }_2$ 是控制输入的变化量，并不直接依赖于状态 $x_{t-1}$，雅可比矩阵 $G_t$ 可以表示为：

$$G_t=\frac{\partial }{\partial x}\left[\begin{array}{c}x+(\Delta {\mu }_1\cos (\theta )-\Delta {\mu }_2\sin (\theta ))\\ y+(\Delta {\mu }_1\sin (\theta )+\Delta {\mu }_2\cos (\theta ))\\ \theta +\Delta \theta \end{array}\right]=\left[\begin{array}{ccc}1& 0& -\Delta {\mu }_1\sin ({\theta }_{t-1})-\Delta {\mu }_2\cos ({\theta }_{t-1})\\ 0& 1& \Delta {\mu }_1\cos ({\theta }_{t-1})-\Delta {\mu }_2\sin ({\theta }_{t-1})\\ 0& 0& 1\end{array}\right]$$

此雅可比矩阵 $G_t$ 反映了当前状态对下一时刻状态预测的依赖性，将被用于状态协方差矩阵${\Sigma }_t$的更新：

$${\Sigma }_{t|t-1}=G_t{\Sigma }_{t-1|t-1}{G}_t^T+F_x{R}_t{F}_x^T$$

其中 $R_t$ 是过程噪声的协方差矩阵，代表了预测模型中的不确定性。$F_t$是一个空间映射矩阵，除了左上角对应机器人位姿的3乘3矩阵为单位阵，其余都置0。虽然运动过程仅对机器人位姿进行更新，但是机器人和每个地标位置之间的相关性同样会被更新。

观测修正

对于所有观测到的特征 $z_t^i$，我们首先检查地标 $j$ 是否是新观测到的。如果是，则初始化该地标的状态，并对应扩展状态矩阵 ${\mu }_t$ 和协方差矩阵 ${\Sigma }_t$。状态向量 ${\mu }_t$ 增加地标的横纵坐标值，而对应的协方差矩阵初始化为无穷。状态向量初始化时将地标距离 $r_t^i$ 和地表方向 ${\varphi }_t^i$ 转为全局坐标：

$$\begin{array}{rl}{\mu }_{j,x}& ={\mu }_{t,x}+r_t^i\cos ({\varphi }_t^i+{\mu }_{t,\theta })\\ {\mu }_{j,y}& ={\mu }_{t,y}+r_t^i\sin ({\varphi }_t^i+{\mu }_{t,\theta })\end{array}$$

计算预测和测量之间的差值：

$$\begin{array}{rl}\delta & =\left[\begin{array}{c}{\delta }_x\\ {\delta }_y\end{array}\right]=\left[\begin{array}{c}{\mu }_{j,x}-{\mu }_{t,x}\\ {\mu }_{j,y}-{\mu }_{t,y}\end{array}\right]\\ q& ={\delta }^T\delta \end{array}$$

计算预测的观测值：

$${\hat{z}}_t^i=\left[\begin{array}{c}\sqrt{q}\\ \text{atan2}({\delta }_y,{\delta }_x)-{\mu }_{t,\theta }\end{array}\right]$$

构建雅克比矩阵 $H_t^i$，$F_{x,j}$ 是空间映射矩阵，除了机器人位姿和地标 j 的位姿对应位置为单位矩阵，其余为 0：

$$H_t^i=\frac{1}{q}\left[\begin{array}{ccccc}-\sqrt{q}{\delta }_x& -\sqrt{q}{\delta }_y& 0& \sqrt{q}{\delta }_x& \sqrt{q}{\delta }_y\\ {\delta }_y& -{\delta }_x& -q& -{\delta }_y& {\delta }_x\end{array}\right]F_{x,j}$$

计算卡尔曼增益 $K_t^i$，其中 $Q_t^i$ 是观测误差协方差矩阵：

$$K_t^i={\Sigma }_t{H}_t^{i^T}{\left(H_t^i{\Sigma }_t{H}_t^{i^T}+Q_t^i\right)}^{-1}$$

最后，更新状态向量 ${\mu }_t$ 和协方差矩阵 ${\Sigma }_t$（这里的 ${\mu }_t$ 和 ${\Sigma }_t$ 是由机器人状态和路标状态组成的）：

$${\mu }_t={\mu }_t+K_t^i\left(z_t^i-{\hat{z}}_t^i\right)$$

$${\Sigma }_t=\left(I-K_t^i{H}_t^i\right){\Sigma }_t$$

参考算法

改自概率机器人