文章目录
- 一、什么是代理
- 二、正向代理
- 三、反向代理
- 四、正向和反向代理模拟复现
一、什么是代理
代理服务器英文全称是Proxy Server,其功能就是代理网络用户去取得网络信息。
形象的说:它是网络信息的中转站。在一般情况下,我们使用网络浏览器直接去连接其他Internet站点取得网络信息时,须送出Request信号来得到回答,然后对方再把信息以bit方式传送回来。
代理服务器是介于浏览器和Web服务器之间的一台服务器,有了它之后,浏览器不是直接到Web服务器去取回网页而是向代理服务器发出请求,Request信号会先送到代理服务器,由代理服务器来取回浏览器所需要的信息并传送给你的浏览器。
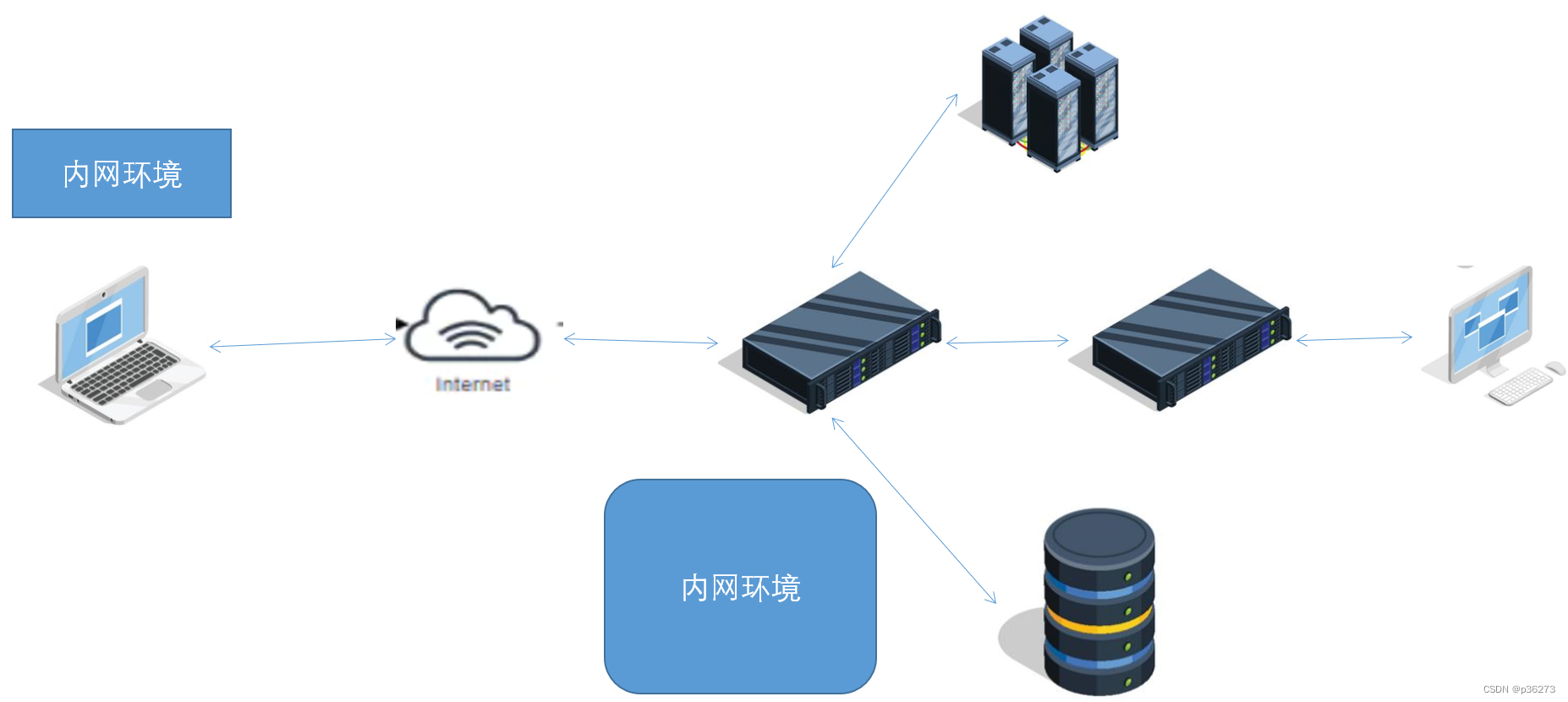
二、正向代理
正向代理即是客户端代理, 代理客户端, 服务端不知道实际发起请求的客户端。正向代理中,proxy和client同属一个LAN,对server透明。
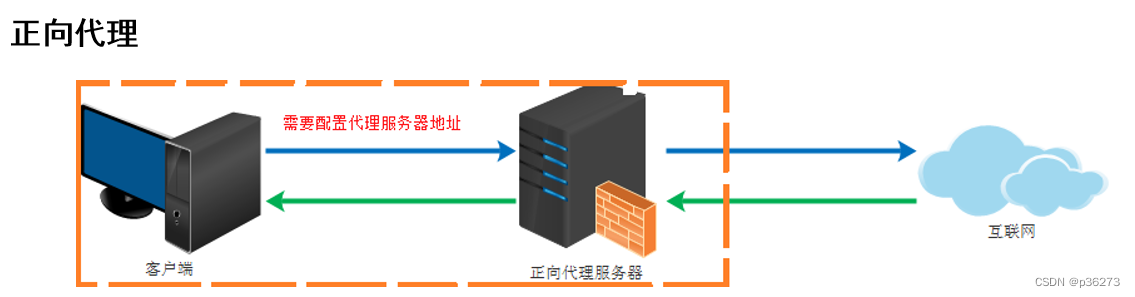
比如我们国内访问谷歌,直接访问访问不到,我们可以通过一个正向代理服务器,请求发到代理服,代理服务器能够访问谷歌,这样由代理去谷歌取到返回数据,再返回给我们,这样我们就能访问谷歌了。
三、反向代理
反向代理即是服务端代理, 代理服务端, 客户端不知道实际提供服务的服务端,反向代理中,proxy和server同属一个LAN,对client透明。
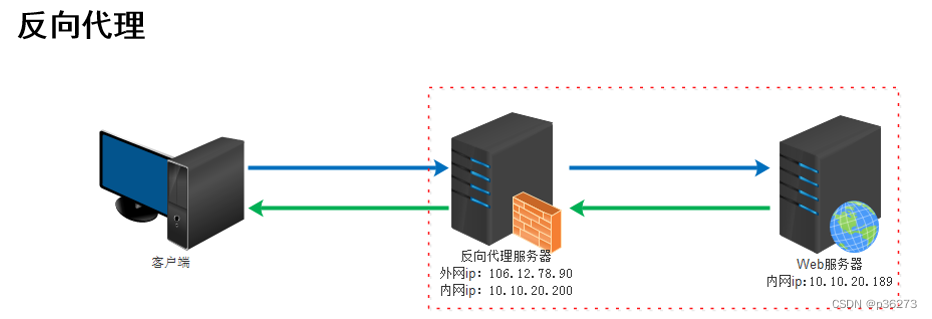
反向代理(Reverse Proxy)实际运行方式是指以代理服务器来接受internet上的连接请求,然后将请求转发给内部网络上的服务器,并将从服务器上得到的结果返回给internet上请求连接的客户端,此时代理服务器对外就表现为一个服务器
四、正向和反向代理模拟复现
正向代理: 正向代理
反向代理: 反向代理
![P1529 [USACO2.4] 回家 Bessie Come Home 题解](https://img-blog.csdnimg.cn/f95ddae62a4e43a68295601c723f92fb.gif#pic_center)