欧拉角(横滚角、俯仰角、偏航角)、旋转矩阵、四元数的转换与解决万向节死锁

1、概述

物体的位姿（位置和方向）的描述方法一般使用两个坐标系来表示，一个是世界坐标系或地面坐标系，这里我都叫做地面坐标系吧，属于参考坐标系；另一个是自身的坐标系，以飞机为例来讲述一些常见的用语，感觉比较合适，这里就叫做机体坐标系，这个会随着自身的变化而发生变化。
如下图所示：

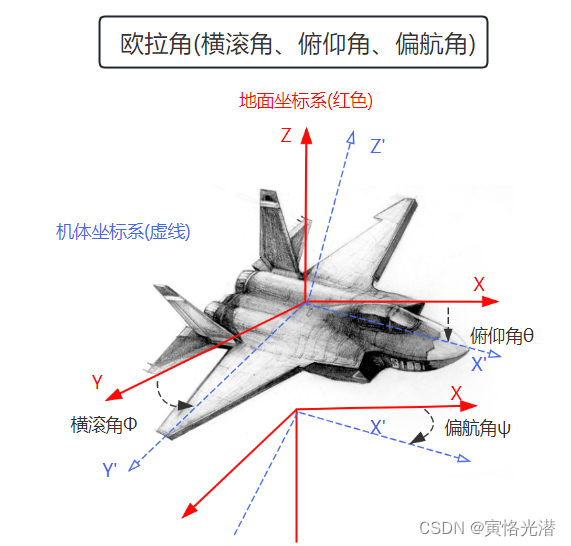
2、机体坐标系

机体坐标系是指固定在飞行器或者飞机上的遵循右手法则的三维正交直角坐标系，其原点位于飞行器的质心。
X'轴永远指向机头,Y'轴指向机身右方，跟X'轴所在的对称平面垂直，Z'轴跟X'轴的所在水平平面垂直。也就是说这个坐标的固定是相对飞机来说的不变化，而上面的地面坐标系是整个的参考坐标，保持固定不变。

3、欧拉角

Euler欧拉角（姿态角）：
机体坐标系与地面坐标系的关系是三个角，反应了飞机相对地面的姿态。

横滚角Φ（roll）：绕X轴旋转。横滚角是指运载体横轴与水平线之间的夹角。也叫滚转角，代表运载体绕纵轴的转动，绕纵轴轴向顺时针转动为正，否则为负，可以想象成飞机做翻滚运动。

俯仰角θ（pitch）：绕Y轴旋转。机体坐标系x轴与水平面的夹角，俯仰角在水平面上面为正，否则为负，可以想象成飞机抬头向上与俯冲向下。

偏航角ψ（yaw）：绕Z轴旋转。相对于纵轴的旋转角度，改变偏航角可以改变飞机的飞行方向，机头往右为正，这个跟平时开车，左转弯右转弯一样。

4、欧拉角转换旋转矩阵

当然这个欧拉角的旋转顺序也是很有关系的，都是描述着一个坐标系到另一个坐标系的变化，也就是说一个坐标系相对于另一个坐标系的位姿可以使用一个旋转矩阵来表示。其旋转矩阵我们来看下推导如下：

5、四元数

四元数，又称欧拉参数，提供另外一种方法来表述三维旋转。四元数方法用在大多数的演算会比较快捷，并能避免一些技术上的问题，如万向节死锁(即当旋转角度接近某些特定值时，欧拉角表示会出现无限循环，换句话说就是两个轴重合，失去一个自由度，然后再旋转也没啥意义了) 现象，因为这些原因，许多高速度三维图形程式制作都使用四元数。当然四元数没有欧拉角来的直观，比较难以理解，这个也是它的缺点。
欧拉角和四元数都是用于描述旋转和方向的方法，但它们在表示旋转的方式和数学结构上有所不同。
对于万向节死锁的情况，可以查看视频来更直观了解：欧拉旋转万向节死锁
四元数是四个自由度，比欧拉角多出一个自由度：
Q=a+bi+cj+dk，其中a,b,c,d是实数，i,j,k是虚数，i²=j²=k²=-1

6、Python示例

6.1、欧拉角转旋转矩阵

import math
import numpy as np
def euler_to_matrix(theta) :R_x = np.array([[1, 0,0],[0,math.cos(theta[0]), -math.sin(theta[0])],[0,math.sin(theta[0]), math.cos(theta[0])]])   R_y = np.array([[math.cos(theta[1]), 0,math.sin(theta[1])],[0,1,0],[-math.sin(theta[1]),0,math.cos(theta[1])]])R_z = np.array([[math.cos(theta[2]), -math.sin(theta[2]),0],[math.sin(theta[2]), math.cos(theta[2]),0],[0,0,1]]) R = np.dot(R_z, np.dot( R_y, R_x ))return R

分别计算绕x、y、z轴的旋转矩阵，然后以某个顺序做点积运算即可。

print(euler_to_matrix([math.pi/3,0,math.pi/6]))
/*
[[ 0.8660254 -0.25       0.4330127][ 0.5        0.4330127 -0.75     ][-0.         0.8660254  0.5      ]]
*/

使用transforms3d或者scipy里面的库，分别来验证下，答案是正确的：

import transforms3d as tfs
print(tfs.euler.euler2mat(math.pi/3,0,math.pi/6,"sxyz"))
print(np.degrees(tfs.euler.mat2euler(euler_to_matrix([math.pi/3,0,math.pi/6]),"sxyz"))) #[60. -0. 30.]//使用弧度制
from scipy.spatial.transform import Rotation as R
print(R.from_euler('xyz', [math.pi/3,0,math.pi/6], degrees=False).as_matrix())
print(np.degrees(R.from_matrix(euler_to_matrix([math.pi/3,0,math.pi/6])).as_euler('xyz'))) #[60.  0. 30.]
//使用角度制
print(R.from_euler('xyz', [60,0,30], degrees=True).as_matrix())

一般我们都是以弧度为标准，当然有些情况为了直观，我们也可以转成角度来运算。

6.2、欧拉角转四元数

import mathdef euler_to_quaternion(roll, pitch, yaw):cy = math.cos(yaw * 0.5)sy = math.sin(yaw * 0.5)cr = math.cos(roll * 0.5)sr = math.sin(roll * 0.5)cp = math.cos(pitch * 0.5)sp = math.sin(pitch * 0.5)w = cy * cr * cp + sy * sr * spx = cy * sr * cp - sy * cr * spy = cy * cr * sp + sy * sr * cpz = sy * cr * cp - cy * sr * spreturn w, x, y, zprint(euler_to_quaternion(math.pi/3,0,math.pi/6))
#(0.8365163037378079, 0.4829629131445341, 0.12940952255126034, 0.2241438680420134)print(tfs.euler.euler2quat(math.pi/3,0,math.pi/6,"sxyz"))
#[0.8365163  0.48296291 0.12940952 0.22414387]print(euler_to_quaternion(math.pi/3,math.pi,math.pi/2))
#(0.3535533905932738, -0.6123724356957946, 0.6123724356957946, -0.3535533905932737)print(tfs.euler.euler2quat(math.pi/3,math.pi,math.pi/2,"sxyz"))
#array([ 0.35355339, -0.61237244,  0.61237244, -0.35355339])

6.3、四元数转旋转矩阵

#x, y ,z ,w
def quaternion_to_rotation_matrix(q):rot_matrix = np.array([[1.0 - 2 * (q[1] * q[1] + q[2] * q[2]), 2 * (q[0] * q[1] - q[3] * q[2]), 2 * (q[3] * q[1] + q[0] * q[2])],[2 * (q[0] * q[1] + q[3] * q[2]), 1.0 - 2 * (q[0] * q[0] + q[2] * q[2]), 2 * (q[1] * q[2] - q[3] * q[0])],[2 * (q[0] * q[2] - q[3] * q[1]), 2 * (q[1] * q[2] + q[3] * q[0]), 1.0 - 2 * (q[0] * q[0] + q[1] * q[1])]],dtype=q.dtype)return rot_matrixr_matrix=quaternion_to_rotation_matrix(np.array([0.4829629,0.12940952,0.22414387,0.8365163]))
print(r_matrix)
/*
[[ 8.66025403e-01 -2.50000007e-01  4.33012693e-01][ 4.99999996e-01  4.33012726e-01 -7.49999975e-01][ 1.23449401e-09  8.66025378e-01  5.00000027e-01]]
*/

6.4、旋转矩阵转欧拉角

def rotation_matrix_to_euler(R) :sy = math.sqrt(R[0,0] * R[0,0] +  R[1,0] * R[1,0])singular = sy < 1e-6if  not singular :x = math.atan2(R[2,1] , R[2,2])y = math.atan2(-R[2,0], sy)z = math.atan2(R[1,0], R[0,0])else :x = math.atan2(-R[1,2], R[1,1])y = math.atan2(-R[2,0], sy)z = 0return np.array([x, y, z])print(rotation_matrix_to_euler(r_matrix))
//弧度
#[ 1.04719751e+00 -1.23449401e-09  5.23598772e-01]
print(np.degrees(rotation_matrix_to_euler(r_matrix)))
//角度
#[ 5.99999979e+01 -7.07312966e-08  2.99999998e+01]