总结

• 做了后4题。https://www.lanqiao.cn/oj-contest/challenge-3/
• T5 二分
• T6 数学公式
• T7 博弈
• T8 优化建图+dij
• 

深秋的苹果

链接: 深秋的苹果

1. 题目描述

2. 思路分析

• 二分即可。但这题上界很大，无脑1e18会wa，实测2e18能过。

3. 代码实现

#       ms
def solve():n, m = RI()arr = RILST()p = s = 0for v in arr:p += v*ss += vdef ok(x):cnt = 1s = c =0for v in arr:c += v * ss += vif c > x:c = 0s = vcnt += 1if cnt > m:return Falsereturn Trueprint(lower_bound(0, p, key=ok))# print(lower_bound(0, 2*10**18, key=ok))

鲜花之海

链接: 鲜花之海

1. 题目描述

2. 思路分析

• 画一下矩阵图，发现按照和可以分为左上半区和右下半区，是一个分段函数。
• 那么分类讨论，看看k落在第几条↙斜线上，由于是等差数列求和，需要解一元二次方程。

3. 代码实现

"""
x*(x+1)//2 <= k
x^2 + x  - k*2<= 0
x <= (-1 +- sqrt(1 + 4 * k*2))/2(n-1+n-1-x+1)*x//2 <= k
"""#       ms
def solve():n, k = RI()left = (1 + n - 1) * (n - 1) // 2mid = nif k <= left + mid:x = int((-1 + sqrt(1 + 4 * k * 2)) / 2)s = x * (x + 1) // 2h = x + 1if s == k:print(h - 1, 1)else:h += 1k -= sprint(k, h - k)else:k -= left + mid# print(left,mid,k)x = int((2 * n - 1 - sqrt((2 * n - 1) ** 2 - 4 * 2 * k)) / 2)s = (n - 1 + n - 1 - x + 1) * x // 2# print(x,s)h = n + x + 1if s == k:print(n, h - n)else:h += 1k -= s# print(x,h,k)print(2 + x + k - 1, h - (2 + x + k - 1))

斐波拉契跳跃

链接: 斐波拉契跳跃

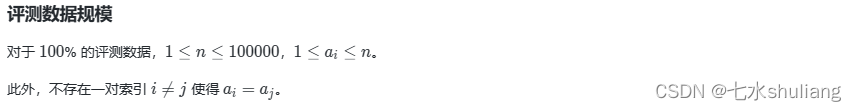
2. 思路分析

• 博弈题优先考虑记忆化搜索。
• 这题转移和状态都是走斐波那契数列的，所以状态和转移都很少，因此可以过。

3. 代码实现

fib = [0, 1, 2]
while fib[-1] <= 10 ** 5:fib.append(fib[-1] + fib[-2])
pfib = {v: i for i, v in enumerate(fib)}#       ms
def solve():n, = RI()a = RILST()pos = [0] * nfor i, v in enumerate(a):pos[v - 1] = i@lru_cache(None)def dfs(p, d):  # 从p位置出发，上一步长d时，能否赢for v in fib[pfib[d] + 1:]:if v >= n: breakif p + v < n and a[p + v] > a[p]:if not dfs(p + v, v):  # 对方不能赢return Trueif p - v >= 0 and a[p - v] > a[p]:if not dfs(p - v, v):return Truereturn Falsefor st in range(n):print(['Little Qiao', 'Little Lan'][dfs(st, 0)])

星石传送阵

链接: 星石传送阵

2. 思路分析

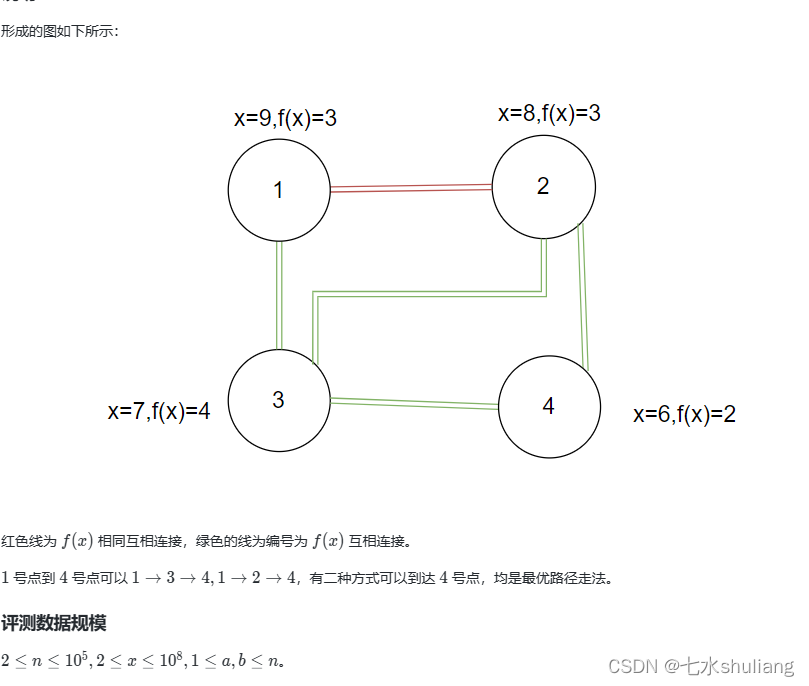
• 题面太乱了，省流：每个位置i的f(x)是x分解质因数求和modn+1；i和f可以互达；f相同的i也可以互达。问a到b最短路。
• 那么由于有很多节点的f可能是相同的，他们都可以互达的话就是稠密图，考虑增加中间虚拟节点连接他们。
• 由于f是对n取模后+1的，那么新节点可以用[n+1,2n]这些节点。
• 那么u->f->v这算1次跳跃，每条边边权应该是0.5；正常互条的节点边权是1；实现时全部乘2避免处理浮点数。

---

• 另一种思路，按f分组，直接BFS，可以省去一个log。
• bfs时，对每个节点处理本组f记录的邻居后，直接移除这整个组，因为他们已经访问过了。这样就可以避免稠密图的边过多造成的TLE。

3. 代码实现

class PrimeTable:def __init__(self, n: int) -> None:self.n = nself.primes = primes = []  # 所有n以内的质数self.min_div = min_div = [0] * (n + 1)  # md[i]代表i的最小(质)因子min_div[1] = 1# 欧拉筛O(n)，顺便求出min_divfor i in range(2, n + 1):if not min_div[i]:primes.append(i)min_div[i] = ifor p in primes:if i * p > n: breakmin_div[i * p] = pif i % p == 0:breakdef prime_factorization(self, x: int):"""分解质因数，复杂度1. 若x>n则需要从2模拟到sqrt(x)，如果中间x降到n以下则走2；最坏情况，不含低于n的因数，则需要开方复杂度2. 否则x质因数的个数，那么最多就是O(lgx)"""n, min_div = self.n, self.min_divfor p in range(2, int(x ** 0.5) + 1):if x <= n: breakif x % p == 0:cnt = 0while x % p == 0: cnt += 1; x //= pyield p, cntwhile 1 < x <= n:p, cnt = min_div[x], 0while x % p == 0: cnt += 1; x //= pyield p, cntif x >= n and x > 1:yield x, 1pt = PrimeTable(10 ** 6)def solve():n, a, b = RI()arr = RILST()g = [[] for _ in range(2 * n + 3)]for i, v in enumerate(arr, start=1):f = sum(x * y for x, y in pt.prime_factorization(v)) % n + 1ff = f + n + 1  # 跳到虚拟节点，边权0.5，实际处理边权全部乘2g[ff].append((i, 1))g[i].append((ff, 1))if f <= n:  # 互跳节点g[i].append((f, 2))g[f].append((i, 2))q = [(0, a)]dis = [inf] * (2 * n + 3)dis[a] = 0while q:# print(q)c, u = heappop(q)if c > dis[u]: continueif u == b:return print(c // 2)for v, w in g[u]:if c + w < dis[v]:dis[v] = c + wheappush(q, (c + w, v))print(-1)

六、参考链接

• 无