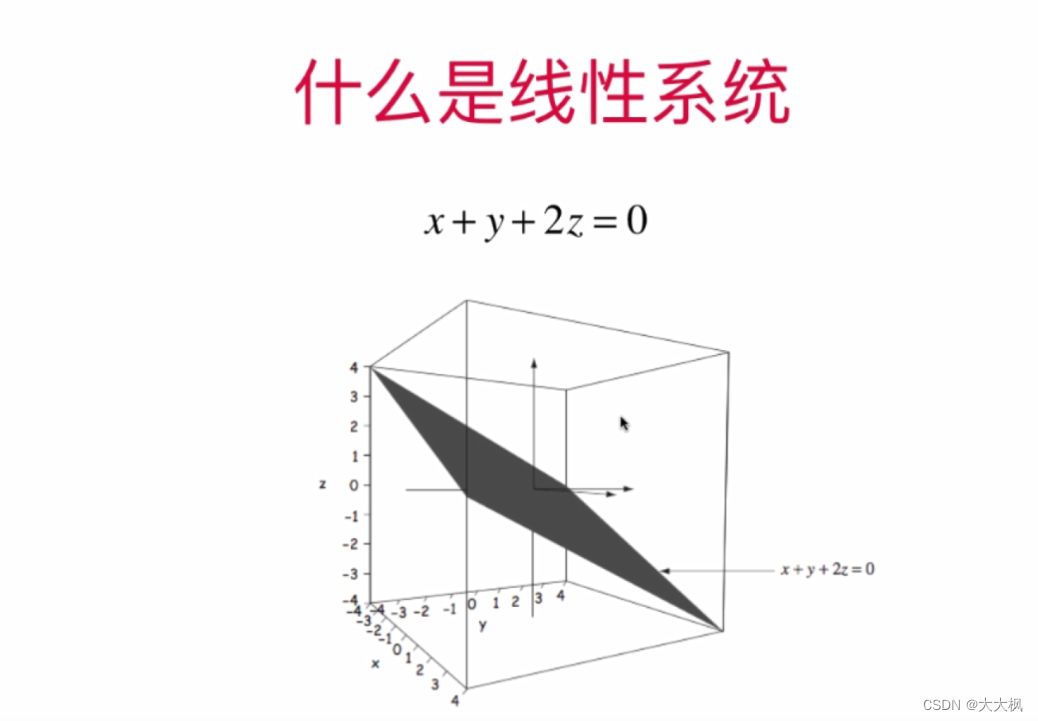
1 线性系统

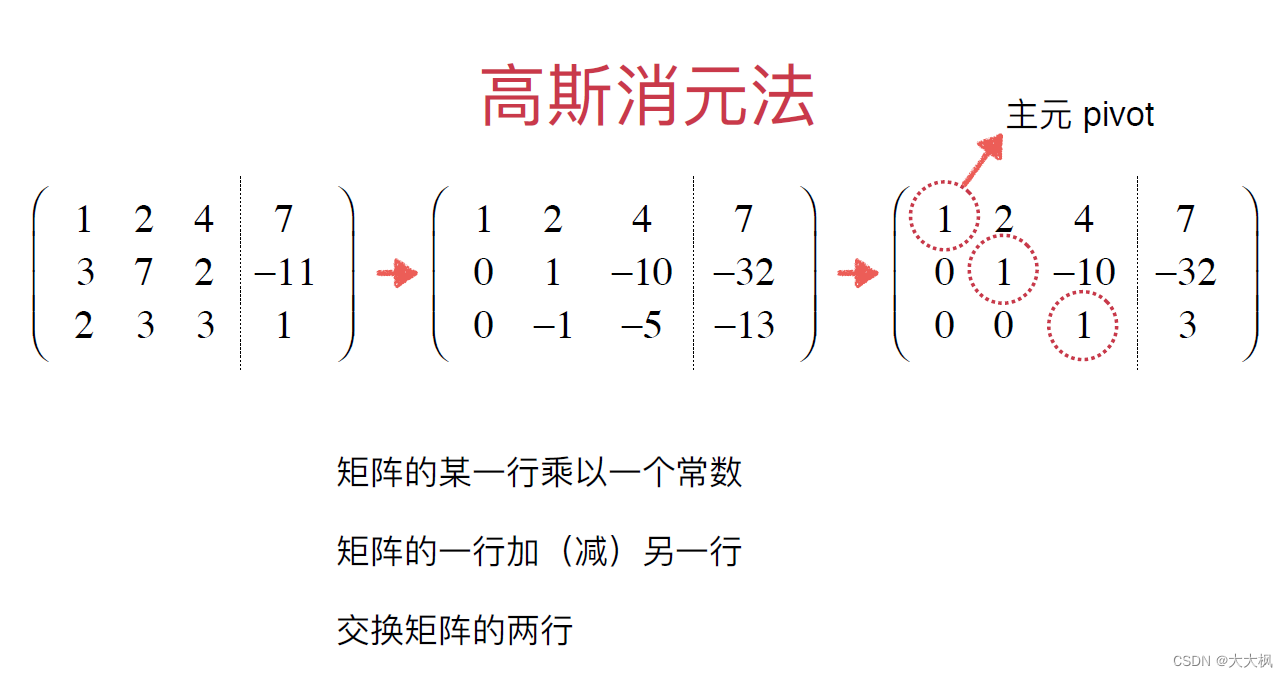
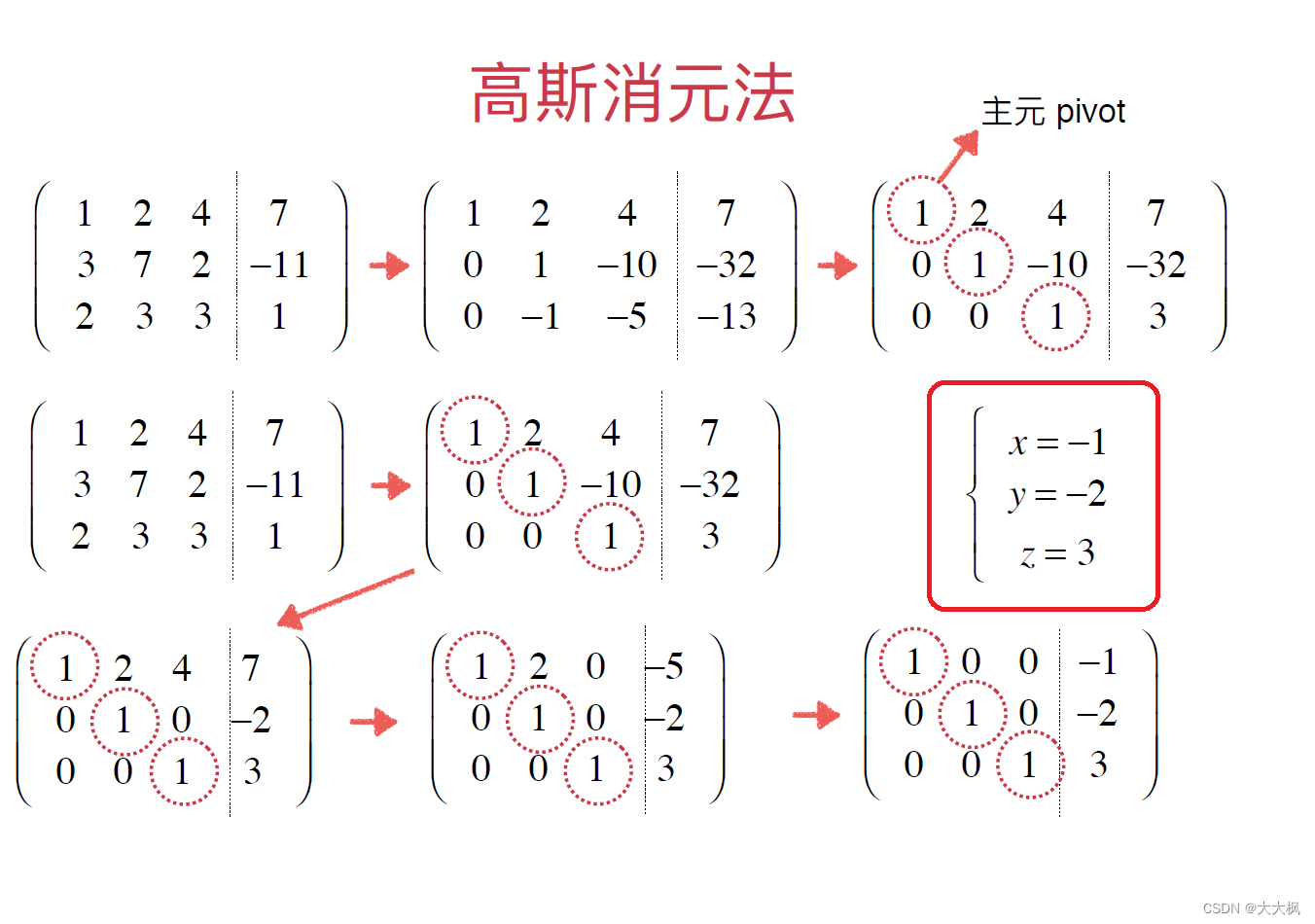
2 高斯-jordon消元法的实现

2.1 Matrix

from .Vector import Vectorclass Matrix:def __init__(self, list2d):self._values = [row[:] for row in list2d]@classmethoddef zero(cls, r, c):"""返回一个r行c列的零矩阵"""return cls([[0] * c for _ in range(r)])@classmethoddef identity(cls, n):"""返回一个n行n列的单位矩阵"""m = [[0]*n for _ in range(n)]for i in range(n):m[i][i] = 1;return cls(m)def T(self):"""返回矩阵的转置矩阵"""return Matrix([[e for e in self.col_vector(i)]for i in range(self.col_num())])def __add__(self, another):"""返回两个矩阵的加法结果"""assert self.shape() == another.shape(), \"Error in adding. Shape of matrix must be same."return Matrix([[a + b for a, b in zip(self.row_vector(i), another.row_vector(i))]for i in range(self.row_num())])def __sub__(self, another):"""返回两个矩阵的减法结果"""assert self.shape() == another.shape(), \"Error in subtracting. Shape of matrix must be same."return Matrix([[a - b for a, b in zip(self.row_vector(i), another.row_vector(i))]for i in range(self.row_num())])def dot(self, another):"""返回矩阵乘法的结果"""if isinstance(another, Vector):# 矩阵和向量的乘法assert self.col_num() == len(another), \"Error in Matrix-Vector Multiplication."return Vector([self.row_vector(i).dot(another) for i in range(self.row_num())])if isinstance(another, Matrix):# 矩阵和矩阵的乘法assert self.col_num() == another.row_num(), \"Error in Matrix-Matrix Multiplication."return Matrix([[self.row_vector(i).dot(another.col_vector(j)) for j in range(another.col_num())]for i in range(self.row_num())])def __mul__(self, k):"""返回矩阵的数量乘结果: self * k"""return Matrix([[e * k for e in self.row_vector(i)]for i in range(self.row_num())])def __rmul__(self, k):"""返回矩阵的数量乘结果: k * self"""return self * kdef __truediv__(self, k):"""返回数量除法的结果矩阵：self / k"""return (1 / k) * selfdef __pos__(self):"""返回矩阵取正的结果"""return 1 * selfdef __neg__(self):"""返回矩阵取负的结果"""return -1 * selfdef row_vector(self, index):"""返回矩阵的第index个行向量"""return Vector(self._values[index])def col_vector(self, index):"""返回矩阵的第index个列向量"""return Vector([row[index] for row in self._values])def __getitem__(self, pos):"""返回矩阵pos位置的元素"""r, c = posreturn self._values[r][c]def size(self):"""返回矩阵的元素个数"""r, c = self.shape()return r * cdef row_num(self):"""返回矩阵的行数"""return self.shape()[0]__len__ = row_numdef col_num(self):"""返回矩阵的列数"""return self.shape()[1]def shape(self):"""返回矩阵的形状: (行数， 列数)"""return len(self._values), len(self._values[0])def __repr__(self):return "Matrix({})".format(self._values)__str__ = __repr__

2.2 Vector

import math
from ._globals import EPSILON
class Vector:def __init__(self, lst):"""__init__ 代表类的构造函数双下划线开头的变量 例如_values,代表类的私有成员lst是个引用，list(lst)将值复制一遍，防止用户修改值"""self._values = list(lst)def underlying_list(self):"""返回向量的底层列表"""return self._values[:]def dot(self, another):"""向量点乘，返回结果标量"""assert len(self) == len(another), \"Error in dot product. Length of vectors must be same."return sum(a * b for a, b in zip(self, another))def norm(self):"""返回向量的模"""return math.sqrt(sum(e**2 for e in self))def normalize(self):"""归一化，规范化返回向量的单位向量此处设计到了除法: def __truediv__(self, k):"""if self.norm() < EPSILON:raise ZeroDivisionError("Normalize error! norm is zero.")return Vector(self._values) / self.norm()# return 1 / self.norm() * Vector(self._values)# return Vector([e / self.norm() for e in self])def __truediv__(self, k):"""返回数量除法的结果向量：self / k"""return (1 / k) * self@classmethoddef zero(cls, dim):"""返回一个dim维的零向量@classmethod 修饰符对应的函数不需要实例化，不需要 self 参数，但第一个参数需要是表示自身类的cls参数，可以来调用类的属性，类的方法，实例化对象等。"""return cls([0] * dim)def __add__(self, another):"""向量加法，返回结果向量"""assert len(self) == len(another), \"Error in adding. Length of vectors must be same."# return Vector([a + b for a, b in zip(self._values, another._values)])return Vector([a + b for a, b in zip(self, another)])def __sub__(self, another):"""向量减法，返回结果向量"""assert len(self) == len(another), \"Error in subtracting. Length of vectors must be same."return Vector([a - b for a, b in zip(self, another)])def __mul__(self, k):"""返回数量乘法的结果向量：self * k"""return Vector([k * e for e in self])def __rmul__(self, k):"""返回数量乘法的结果向量：k * selfself本身就是一个列表"""return self * kdef __pos__(self):"""返回向量取正的结果向量"""return 1 * selfdef __neg__(self):"""返回向量取负的结果向量"""return -1 * selfdef __iter__(self):"""返回向量的迭代器"""return self._values.__iter__()def __getitem__(self, index):"""取向量的第index个元素"""return self._values[index]def __len__(self):"""返回向量长度（有多少个元素）"""return len(self._values)def __repr__(self):"""打印显示：Vector([5, 2])"""return "Vector({})".format(self._values)def __str__(self):"""打印显示：(5, 2)"""return "({})".format(", ".join(str(e) for e in self._values))

2.3 线性系统

from .Matrix import Matrix
from .Vector import Vectorclass LinearSystem:def __init__(self, A, b):assert A.row_num() == len(b), "row number of A must be equal to the length of b"self._m = A.row_num()self._n = A.col_num()assert self._m == self._n  # TODO: no this restrictionself.Ab = [Vector(A.row_vector(i).underlying_list() + [b[i]])for i in range(self._m)]def _max_row(self, index_i, index_j, n):best, ret = abs(self.Ab[index_i][index_j]), index_ifor i in range(index_i + 1, n):if abs(self.Ab[i][index_j]) > best:best, ret = abs(self.Ab[i][index_j]), ireturn retdef _forward(self):n = self._mfor i in range(n):# Ab[i][i]为主元max_row = self._max_row(i, i, n)self.Ab[i], self.Ab[max_row] = self.Ab[max_row], self.Ab[i]# 将主元归为一self.Ab[i] = self.Ab[i] / self.Ab[i][i]  # TODO: self.Ab[i][i] == 0?for j in range(i + 1, n):self.Ab[j] = self.Ab[j] - self.Ab[j][i] * self.Ab[i]def _backward(self):n = self._mfor i in range(n - 1, -1, -1):# Ab[i][i]为主元for j in range(i - 1, -1, -1):self.Ab[j] = self.Ab[j] - self.Ab[j][i] * self.Ab[i]def gauss_jordan_elimination(self):self._forward()self._backward()def fancy_print(self):for i in range(self._m):print(" ".join(str(self.Ab[i][j]) for j in range(self._n)), end=" ")print("|", self.Ab[i][-1])

3 行最简形式

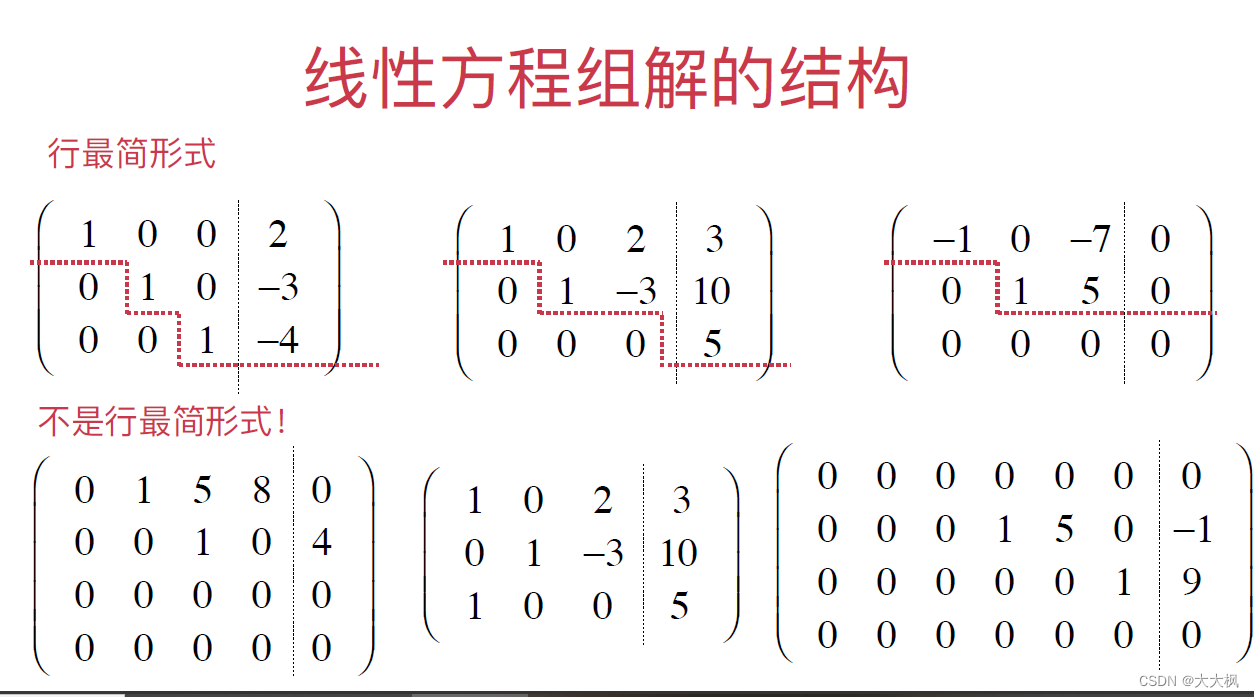
4 线性方程组的结构

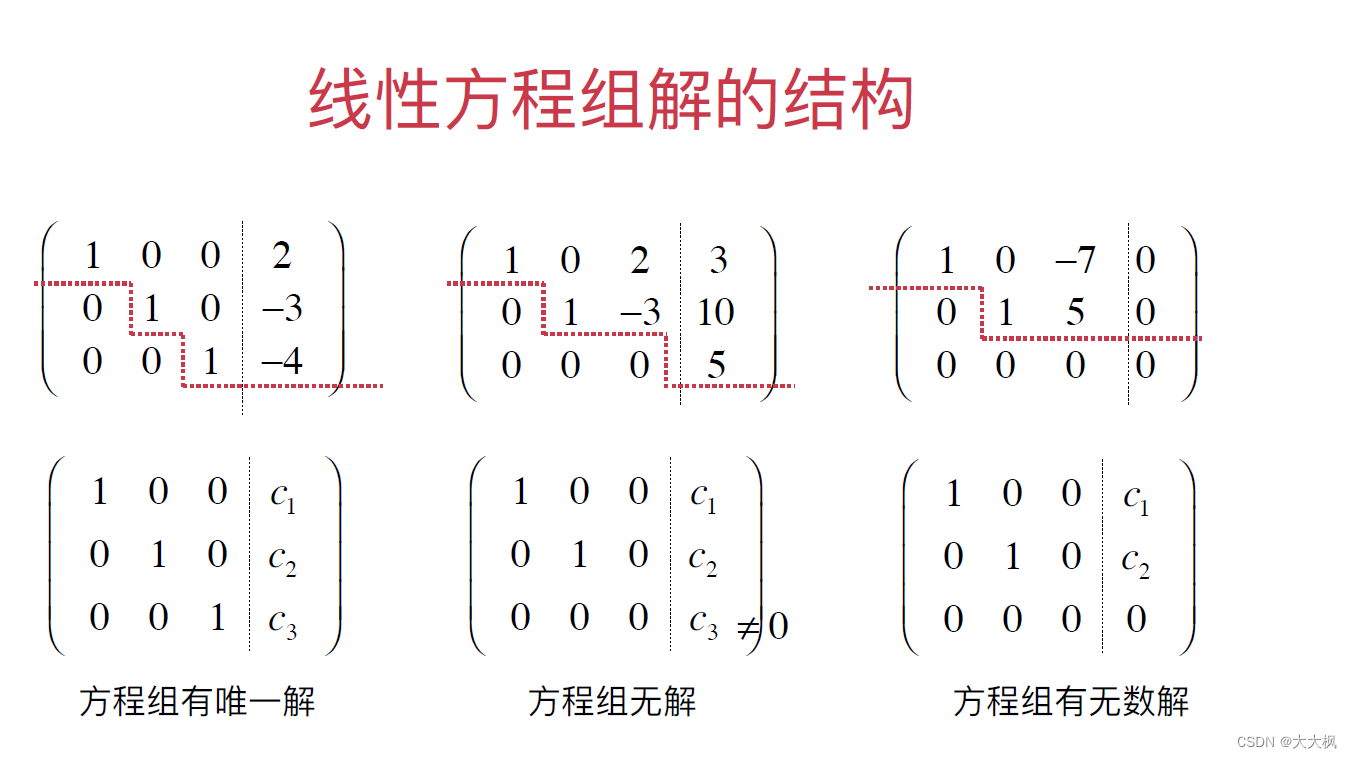
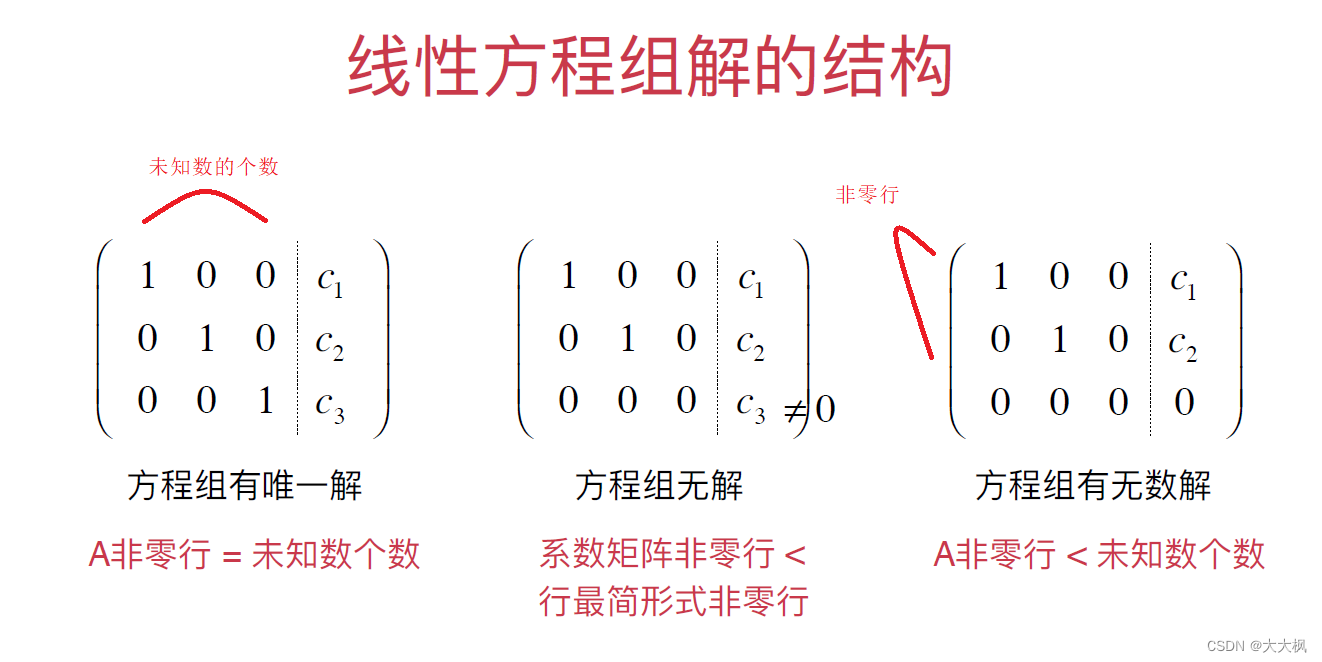
5 线性方程组-通用高斯消元的实现

5.1 global

# 包中的变量，但是对包外不可见，因此使用“_”开头
EPSILON = 1e-8def is_zero(x):return abs(x) < EPSILONdef is_equal(a, b):return abs(a - b) < EPSILON

5.2 Vector-引入is_zero

import math
from ._globals import is_zero
class Vector:def __init__(self, lst):"""__init__ 代表类的构造函数双下划线开头的变量 例如_values,代表类的私有成员lst是个引用，list(lst)将值复制一遍，防止用户修改值"""self._values = list(lst)def underlying_list(self):"""返回向量的底层列表"""return self._values[:]def dot(self, another):"""向量点乘，返回结果标量"""assert len(self) == len(another), \"Error in dot product. Length of vectors must be same."return sum(a * b for a, b in zip(self, another))def norm(self):"""返回向量的模"""return math.sqrt(sum(e**2 for e in self))def normalize(self):"""归一化，规范化返回向量的单位向量此处设计到了除法: def __truediv__(self, k):"""if is_zero(self.norm()):raise ZeroDivisionError("Normalize error! norm is zero.")return Vector(self._values) / self.norm()# return 1 / self.norm() * Vector(self._values)# return Vector([e / self.norm() for e in self])def __truediv__(self, k):"""返回数量除法的结果向量：self / k"""return (1 / k) * self@classmethoddef zero(cls, dim):"""返回一个dim维的零向量@classmethod 修饰符对应的函数不需要实例化，不需要 self 参数，但第一个参数需要是表示自身类的cls参数，可以来调用类的属性，类的方法，实例化对象等。"""return cls([0] * dim)def __add__(self, another):"""向量加法，返回结果向量"""assert len(self) == len(another), \"Error in adding. Length of vectors must be same."# return Vector([a + b for a, b in zip(self._values, another._values)])return Vector([a + b for a, b in zip(self, another)])def __sub__(self, another):"""向量减法，返回结果向量"""assert len(self) == len(another), \"Error in subtracting. Length of vectors must be same."return Vector([a - b for a, b in zip(self, another)])def __mul__(self, k):"""返回数量乘法的结果向量：self * k"""return Vector([k * e for e in self])def __rmul__(self, k):"""返回数量乘法的结果向量：k * selfself本身就是一个列表"""return self * kdef __pos__(self):"""返回向量取正的结果向量"""return 1 * selfdef __neg__(self):"""返回向量取负的结果向量"""return -1 * selfdef __iter__(self):"""返回向量的迭代器"""return self._values.__iter__()def __getitem__(self, index):"""取向量的第index个元素"""return self._values[index]def __len__(self):"""返回向量长度（有多少个元素）"""return len(self._values)def __repr__(self):"""打印显示：Vector([5, 2])"""return "Vector({})".format(self._values)def __str__(self):"""打印显示：(5, 2)"""return "({})".format(", ".join(str(e) for e in self._values))

5.3 LinearSystem

from .Matrix import Matrix
from .Vector import Vector
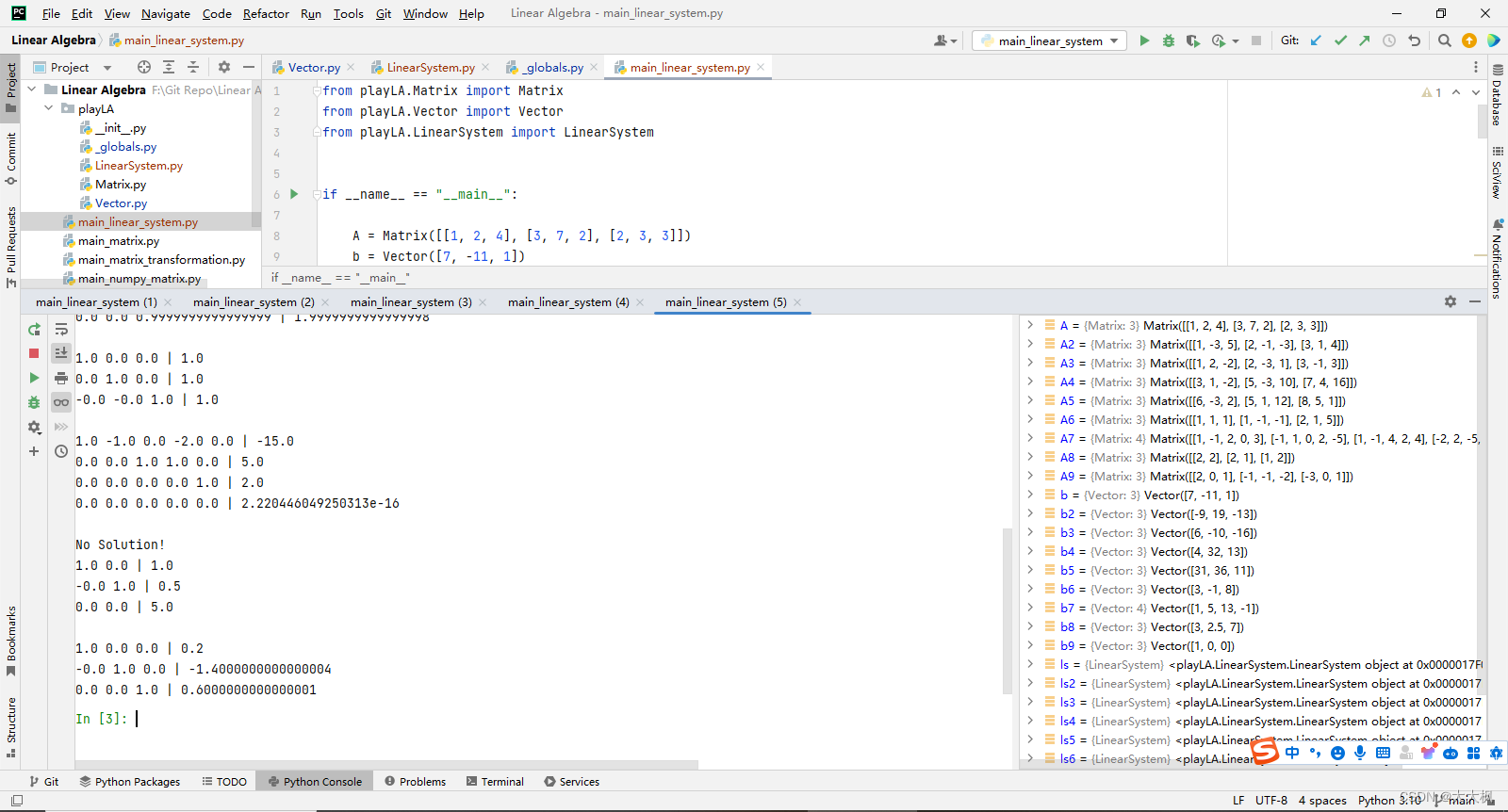
from ._globals import is_zeroclass LinearSystem:def __init__(self, A, b):assert A.row_num() == len(b), "row number of A must be equal to the length of b"self._m = A.row_num()self._n = A.col_num()# assert self._m == self._n  # TODO: no this restrictionself.Ab = [Vector(A.row_vector(i).underlying_list() + [b[i]])for i in range(self._m)]self.pivots = []def _max_row(self, index_i, index_j, n):best, ret = abs(self.Ab[index_i][index_j]), index_ifor i in range(index_i + 1, n):if abs(self.Ab[i][index_j]) > best:best, ret = abs(self.Ab[i][index_j]), ireturn retdef _forward(self):i, k = 0, 0while i < self._m and k < self._n:# 看Ab[i][k]位置是否可以是主元max_row = self._max_row(i, k, self._m)self.Ab[i], self.Ab[max_row] = self.Ab[max_row], self.Ab[i]if is_zero(self.Ab[i][k]):k += 1else:# 将主元归为一self.Ab[i] = self.Ab[i] / self.Ab[i][k]for j in range(i + 1, self._m):self.Ab[j] = self.Ab[j] - self.Ab[j][k] * self.Ab[i]self.pivots.append(k)i += 1def _backward(self):n = len(self.pivots)for i in range(n - 1, -1, -1):k = self.pivots[i]# Ab[i][k]为主元for j in range(i - 1, -1, -1):self.Ab[j] = self.Ab[j] - self.Ab[j][k] * self.Ab[i]def gauss_jordan_elimination(self):"""如果有解，返回True；如果没有解，返回False"""self._forward()self._backward()for i in range(len(self.pivots), self._m):if not is_zero(self.Ab[i][-1]):return Falsereturn Truedef fancy_print(self):for i in range(self._m):print(" ".join(str(self.Ab[i][j]) for j in range(self._n)), end=" ")print("|", self.Ab[i][-1])

5.4 main

from playLA.Matrix import Matrix
from playLA.Vector import Vector
from playLA.LinearSystem import LinearSystemif __name__ == "__main__":A = Matrix([[1, 2, 4], [3, 7, 2], [2, 3, 3]])b = Vector([7, -11, 1])ls = LinearSystem(A, b)ls.gauss_jordan_elimination()ls.fancy_print()print()# [-1, -2, 3]A2 = Matrix([[1, -3, 5], [2, -1, -3], [3, 1, 4]])b2 = Vector([-9, 19, -13])ls2 = LinearSystem(A2, b2)ls2.gauss_jordan_elimination()ls2.fancy_print()print()# [2, -3, -4]A3 = Matrix([[1, 2, -2], [2, -3, 1], [3, -1, 3]])b3 = Vector([6, -10, -16])ls3 = LinearSystem(A3, b3)ls3.gauss_jordan_elimination()ls3.fancy_print()print()# [-2, 1, -3]A4 = Matrix([[3, 1, -2], [5, -3, 10], [7, 4, 16]])b4 = Vector([4, 32, 13])ls4 = LinearSystem(A4, b4)ls4.gauss_jordan_elimination()ls4.fancy_print()print()# [3, -4, 0.5]A5 = Matrix([[6, -3, 2], [5, 1, 12], [8, 5, 1]])b5 = Vector([31, 36, 11])ls5 = LinearSystem(A5, b5)ls5.gauss_jordan_elimination()ls5.fancy_print()print()# [3, -3, 2]A6 = Matrix([[1, 1, 1], [1, -1, -1], [2, 1, 5]])b6 = Vector([3, -1, 8])ls6 = LinearSystem(A6, b6)ls6.gauss_jordan_elimination()ls6.fancy_print()print()# [1, 1, 1]A7 = Matrix([[1, -1, 2, 0, 3],[-1, 1, 0, 2, -5],[1, -1, 4, 2, 4],[-2, 2, -5, -1, -3]])b7 = Vector([1, 5, 13, -1])ls7 = LinearSystem(A7, b7)ls7.gauss_jordan_elimination()ls7.fancy_print()print()A8 = Matrix([[2, 2],[2, 1],[1, 2]])b8 = Vector([3, 2.5, 7])ls8 = LinearSystem(A8, b8)if not ls8.gauss_jordan_elimination():print("No Solution!")ls8.fancy_print()print()A9 = Matrix([[2, 0, 1],[-1, -1, -2],[-3, 0, 1]])b9 = Vector([1, 0, 0])ls9 = LinearSystem(A9, b9)if not ls9.gauss_jordan_elimination():print("No Solution!")ls9.fancy_print()print()