一、内容简介
本文使用Python编写程序,实现2个m * n矩阵的加、减法。具体过程如下:
给定两个m*n矩阵A和B,返回A与B的和或差。
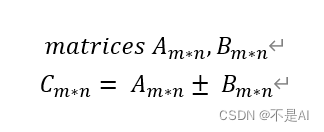
二、求解方法
将两个矩阵对应位置上的元素相加。
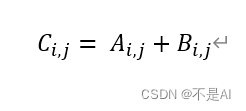
三、Python代码
import numpy as np# 用户输入两个矩阵的维度取值m, n
m = int(input("Enter m: "))
n = int(input("Enter n: "))# (用0)初始化A,B,C3个矩阵,数据类型为浮点值
A = np.zeros((m, n), dtype=float)
B = np.zeros((m, n), dtype=float)
C = np.zeros((m, n), dtype=float)# 用户输入矩阵A
print("Enter matrix A: ")
for i in range(0, m):for j in range(0, n):A[i][j] = float(input())# 用户输入矩阵B
print("Enter matrix B: ")
for i in range(0, m):for j in range(0, n):B[i][j] = float(input())print()
# 用户输入运算类型,输入a代表做加法,s代表做减法
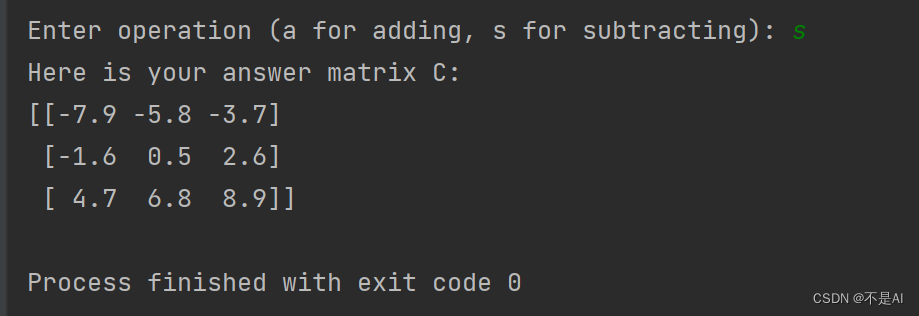
op = input("Enter operation (a for adding, s for subtracting): ")
# 做加法
if op == 'a':for i in range(0, m):for j in range(0, n):C[i][j] = A[i][j] + B[i][j]# 做减法
elif op == 's':for i in range(0, m):for j in range(0, n):C[i][j] = A[i][j] - B[i][j]print("Here is your answer matrix C: ")
print(C)四、程序运行实例
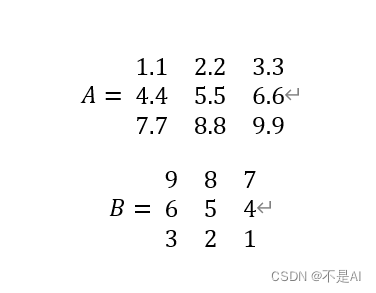
程序运行结果:
A + B:
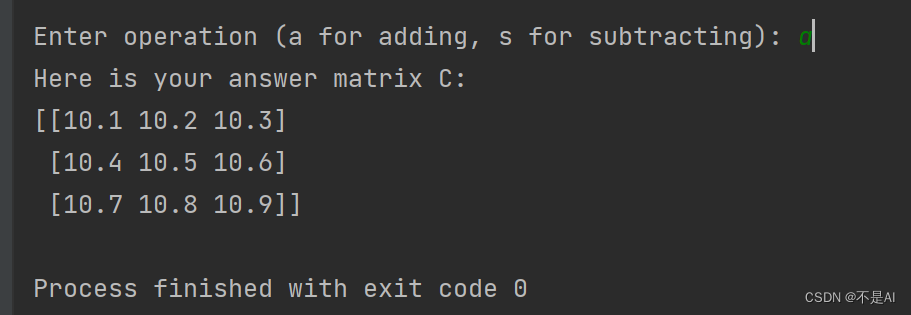
A - B: