所有的LeetCode题解索引，可以看这篇文章——【算法和数据结构】LeetCode题解。

一、题目

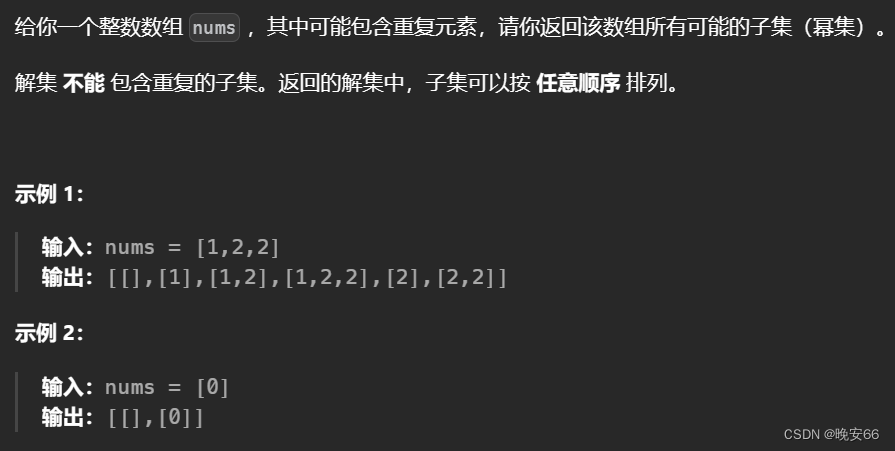
二、78.子集

  思路分析：【算法与数据结构】77、LeetCode组合。本题可以参考77题的组合问题代码，稍加修改即可。本质上还是回溯的三部曲：处理节点、递归、回溯。不过集合问题的k是不固定的，因此每次循环都需要把path的结果加入result中。
  程序如下：

class Solution {
private:vector<vector<int>> result;vector<int> path;void backtracking(const vector<int>& nums, int startIndex) {for (int i = startIndex; i < nums.size(); i++) {path.push_back(nums[i]);	// 处理节点result.push_back(path);backtracking(nums, i + 1);	// 递归path.pop_back();			// 回溯}}
public:vector<vector<int>> subsets(vector<int>& nums) {backtracking(nums, 0);result.push_back({});	// 空集return result;}
};

  进一步的，可以将添加空集的那行代码一起添加到回溯函数当中;

class Solution {
private:vector<vector<int>> result;vector<int> path;void backtracking(const vector<int>& nums, int startIndex) {result.push_back(path);for (int i = startIndex; i < nums.size(); i++) {path.push_back(nums[i]);	// 处理节点			backtracking(nums, i + 1);	// 递归path.pop_back();			// 回溯}}
public:vector<vector<int>> subsets(vector<int>& nums) {backtracking(nums, 0);return result;}
};

复杂度分析：

• 时间复杂度： $O(n\ast 2^n)$。
• 空间复杂度：$O(n)$。

三、90.子集II

  思路分析：【算法与数据结构】40、LeetCode组合总和 II本题解法可以采用和这道题一直的思路，引入一个used数组进行去重。

class Solution {
private:vector<vector<int>> result;vector<int> path;	void backtracking(const vector<int>& nums, int startIndex, vector<bool>& used) {result.push_back(path);		for (int i = startIndex; i < nums.size(); i++) {if (i > 0 && nums[i] == nums[i - 1] && used[i-1] == 0) {continue;		}path.push_back(nums[i]);	// 处理节点	used[i] = true;backtracking(nums, i + 1, used);	// 递归used[i] = false;path.pop_back();			// 回溯}}
public:vector<vector<int>> subsetsWithDup(vector<int>& nums) {vector<bool> used(nums.size(), 0);sort(nums.begin(), nums.end());backtracking(nums, 0, used);return result;}
};

复杂度分析：

• 时间复杂度： $O(n\ast 2^n)$。
• 空间复杂度：$O(n)$。

三、完整代码

// 78子集问题
# include <iostream>
# include <string>
# include <vector>
using namespace std;class Solution {
private:vector<vector<int>> result;vector<int> path;void backtracking(const vector<int>& nums, int startIndex) {result.push_back(path);for (int i = startIndex; i < nums.size(); i++) {path.push_back(nums[i]);	// 处理节点			backtracking(nums, i + 1);	// 递归path.pop_back();			// 回溯}}
public:vector<vector<int>> subsets(vector<int>& nums) {backtracking(nums, 0);return result;}
};int main() {Solution s1;vector<int> nums = { 1, 2, 3 };vector<vector<int>> result = s1.subsets(nums);for (vector<vector<int>>::iterator it = result.begin(); it != result.end(); it++) {for (vector<int>::iterator jt = (*it).begin(); jt != (*it).end(); jt++) {cout << *jt << " ";}cout << endl;}system("pause");return 0;
}

// 90子集II问题
# include <iostream>
# include <string>
# include <vector>
# include <algorithm>
using namespace std;class Solution {
private:vector<vector<int>> result;vector<int> path;	void backtracking(const vector<int>& nums, int startIndex, vector<bool>& used) {result.push_back(path);		for (int i = startIndex; i < nums.size(); i++) {if (i > 0 && nums[i] == nums[i - 1] && used[i-1] == 0) {continue;		}path.push_back(nums[i]);	// 处理节点	used[i] = true;backtracking(nums, i + 1, used);	// 递归used[i] = false;path.pop_back();			// 回溯}}
public:vector<vector<int>> subsetsWithDup(vector<int>& nums) {vector<bool> used(nums.size(), 0);sort(nums.begin(), nums.end());backtracking(nums, 0, used);return result;}
};int main() {Solution s1;vector<int> nums = { 1, 2, 2 };vector<vector<int>> result = s1.subsetsWithDup(nums);for (vector<vector<int>>::iterator it = result.begin(); it != result.end(); it++) {for (vector<int>::iterator jt = (*it).begin(); jt != (*it).end(); jt++) {cout << *jt << " ";}cout << endl;}system("pause");return 0;
}

end