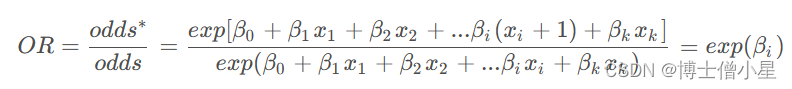一、离散选择模型
莎士比亚曾经说过:To be, or not to be, that is the question,这就是典型的离散选择模型。如果被解释变量时离散的,而非连续的,称为“离散选择模型”。例如,消费者在购买汽车的时候通常会比较几个不同的品牌,如福特、本田、大众等。如果将消费者选择福特汽车记为Y=1,选择本田汽车记为Y=2,选择大众汽车记为Y=3;那么在研究消费者选择何种汽车品牌的时候,由于因变量不是一个连续的变量(Y=1, 2, 3),传统的线性回归模型就有一定的局限。
其它的一些常见的离散选择行为的案例还包括:
化妆品牌的选择:雅诗兰黛、兰蔻、欧莱雅...
就餐地点的选择:餐厅甲、餐厅乙、餐厅丙...
旅游风格的选择:自由游、跟团游、自助游...
居住地点的选择:小区A、小区B、小区C...
出行方式的选择:公交、地铁、打车、合乘、自驾、自行车...
二、Logit模型
在统计学里,「概率(Probability)和Odds都是用来描述某件事情发生的可能性的」。Odds指的是 「事件发生的概率」与 「事件不发生的概率」 之比,可以将Odds称为几率或胜率。
「事件A的Odds」 等于 「事件A出现的次数」 和 「其它(非A)事件出现的次数 之比」;相比之下,「事件A的概率」 等于 「事件A出现的次数」 与 「所有事件的次数」 之比。
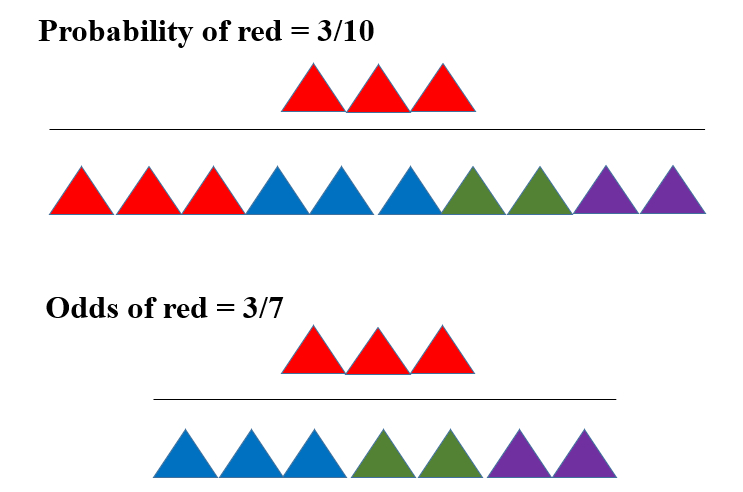
「Odds的对数称之为Logit。」
「从概率P到Odds再到Logit,这就是一个Logit变换。」 Logit 模型可以理解成 Log-it(即it 的自然对数——这里的it指的就是Odds,Logit即the log of an odd)。概率P的取值范围是[0,1],而Logit的取值范围是(-∞,+∞)。概率作为因变量,不能直接套用线性回归模型:
因为线性回归模型的因变量y的范围是,但概率的范围是[0,1]。
由于 Logit的范围是,我们可以将Logit作为因变量,建立线性模型:
方程两边同时exp,可得:
进一步表示为:
Odds Ratio(简称OR)指的是两个几率的比值,称为几率比。举个例子,研究人员怀疑「性别」和「是否会游泳」之间可能存在某种关系,于是按照“性别”和“是否会游泳”对样本进行进划分,结果如下:
| 会游泳 | 不会游泳 | |
|---|---|---|
| 男性 | 100 | 200 |
| 女性 | 100 | 300 |
则男性会游泳的概率为100/300,Odds为100/200,男性会游泳的概率为100/400,Odds为100/300,
则男性相对女性会游泳的Odds Ratio = 100/200/(100/300) =1.5
当OR>1时,分子上的Odds值较大——说明男性会游泳的几率(Odds)更高;若OR=1,则说明性别对是否会游泳没有影响。
三、Logit模型的python实现——采用statsmodels
(一)案例一
以Social_Network_Ads数据为例,演示逻辑回归的Python操作。数据文件一共400条数据,前面四列是用户ID(User ID)、性别(Gender)、年龄(Age)、大致薪水(EstimatedSalary),第五列为是否购买(Purchased),没购买是0,购买是1。数据源文件链接:https://pan.baidu.com/s/1HA6prrhdenNnI76G5QryMw 提取码:zul4。
首先导入相关库。
import pandas as pd
import numpy as np
import statsmodels.formula.api as smf
import statsmodels.api as sm
from patsy import dmatrices
用pandas的「read_csv」函数读取原始数据文件。
data = pd.read_csv(r'C:\Users\mi\Downloads\Social_Network_Ads.csv')
在Spyder的变量浏览器中,可查看data变量。
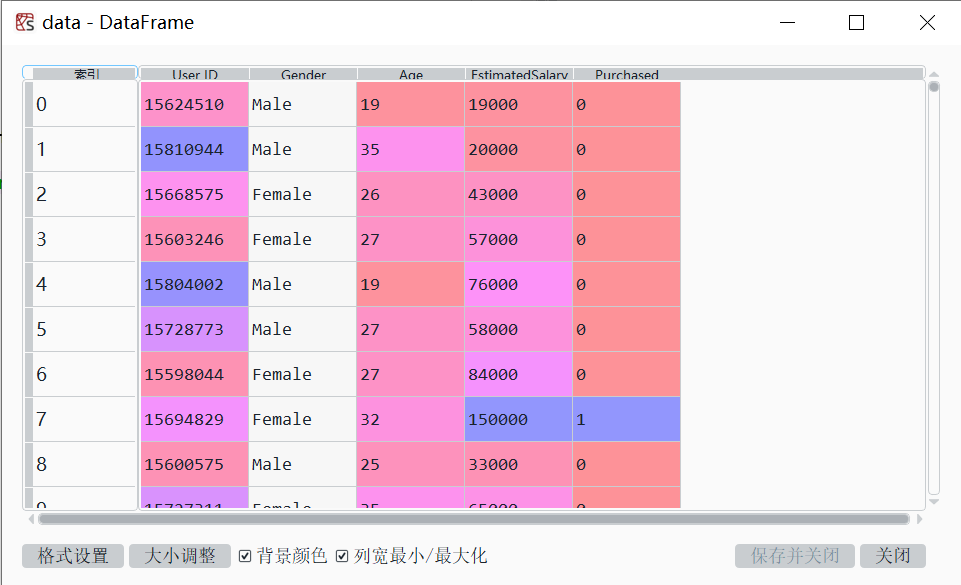
可查看data信息。
print(data.info())
结果为:
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 400 entries, 0 to 399
Data columns (total 5 columns):# Column Non-Null Count Dtype
--- ------ -------------- ----- 0 User ID 400 non-null int64 1 Gender 400 non-null object 2 Age 400 non-null float643 EstimatedSalary 400 non-null float644 Purchased 400 non-null int64
dtypes: float64(2), int64(2), object(1)
memory usage: 15.8+ KB
用DataFrame的「describe」()函数对样本中的各变量做描述性分析,结果如下面所示。我们可以得到每一个变量的出现的频数(count)、均值(mean)、标准差(std)、最大/小值(min/max)、百分位数(25%,50%,75%)等信息。
print(data.describe())
结果为:
User ID Age EstimatedSalary Purchased
count 4.000000e+02 400.000000 400.000000 400.000000
mean 1.569154e+07 37.655000 69742.500000 0.357500
std 7.165832e+04 10.482877 34096.960282 0.479864
min 1.556669e+07 18.000000 15000.000000 0.000000
25% 1.562676e+07 29.750000 43000.000000 0.000000
50% 1.569434e+07 37.000000 70000.000000 0.000000
75% 1.575036e+07 46.000000 88000.000000 1.000000
max 1.581524e+07 60.000000 150000.000000 1.000000
接下来进行Logit回归,有基于公式和基于数组两种方法。
「方法一:基于公式」
import statsmodels.formula.api as smflogit = smf.logit(formula='Purchased ~ Age + EstimatedSalary + Gender', data = data)
results = logit.fit()
print(results.summary())
「方法二:基于数组」
调用Logit() 函数的基本格式为:
sm.Logit(endog,exog)
代码如下:
import statsmodels.api as sm
from patsy import dmatricesy,X = dmatrices('Purchased ~ Age + EstimatedSalary + Gender',data = data,return_type='dataframe')logit = sm.Logit(y,X)
results = logit.fit()
print(results.summary())
方法一和方法二的结果一致,为:
Logit Regression Results
==============================================================================
Dep. Variable: Purchased No. Observations: 400
Model: Logit Df Residuals: 396
Method: MLE Df Model: 3
Date: Sat, 20 Aug 2022 Pseudo R-squ.: 0.4711
Time: 11:33:28 Log-Likelihood: -137.92
converged: True LL-Null: -260.79
Covariance Type: nonrobust LLR p-value: 5.488e-53
===================================================================================coef std err z P>|z| [0.025 0.975]
-----------------------------------------------------------------------------------
Intercept -12.7836 1.359 -9.405 0.000 -15.448 -10.120
Gender[T.Male] 0.3338 0.305 1.094 0.274 -0.264 0.932
Age 0.2370 0.026 8.984 0.000 0.185 0.289
EstimatedSalary 3.644e-05 5.47e-06 6.659 0.000 2.57e-05 4.72e-05
===================================================================================
上表中输出了Logit模型的相关拟合结果。结果包含两部分:上半部分给出了和模型整体相关的信息,包括因变量的名称(Dep. Variable: Purchased)、模型名称(Model: Logit)、拟合方法(Method: MLE 最大似然估计)等信息;下半部分则给出了和每一个系数相关的信息,包括系数的估计值(coef)、标准误(std err)、z统计量的值、显著水平(P>|z|)和95%置信区间。
根据上表可以得到本例中Logit模型的具体形式:
Logit模型变量的系数是指:「自变量每变化一个单位,几率(Odds)的对数的变化值」。在本例中,以变量「Age」的系数为例,其解读方式为:当其它变量保持不变时,申请者的Age年龄每增加一岁,其购买汽车的对数几率增加0.2370(绝对数),对数几率并不易直观理解。由于取对数约等于百分比的变化,故可理解为几率约增加23.70%(相对数)。
假设变化一单位,从变为,记几率odd的新值为,则可根据新几率与原几率odd的比率定义几率比。
or = np.exp(results.params)
print(or)
结果为:
Intercept 0.000003
Gender[T.Male] 1.396324
Age 1.267402
EstimatedSalary 1.000036
dtype: float64
在本例中,以变量「Age」的OR为例,其解读方式为:当其它变量保持不变时,申请者的Age年龄每增加一岁,其购买汽车的几率变为原来的1.267倍,即几率增加了26.7%。
如果想计算每个变量的“边际效应”,可使用get_margeff()方法,并将所得结果用summary()方法展示。
什么是边际效应呢?即,概率对自变量求导数。
get_margeff(at='overall', method='dydx', atexog=None, dummy=False, count=False)
其参数说明如下:
| 参数 | 说明 |
|---|---|
| at | ‘overall’, 平均边际效应,默认. ‘mean’, 样本均值处的边际效应. ‘median’, 样本中值处的边际效应. |
| method | 'dydx’ - dy/dx, ‘eyex’ - d(lny)/d(lnx) ,‘dyex’ - dy/d(lnx) ,‘eydx’ - d(lny)/dx |
计算平均边际效应:
margeff = results.get_margeff()
print(margeff.summary())
结果如下:
=====================================
Dep. Variable: Purchased
Method: dydx
At: overall
===================================================================================dy/dx std err z P>|z| [0.025 0.975]
-----------------------------------------------------------------------------------
Gender[T.Male] 0.0368 0.034 1.099 0.272 -0.029 0.103
Age 0.0262 0.001 18.674 0.000 0.023 0.029
EstimatedSalary 4.022e-06 4.55e-07 8.840 0.000 3.13e-06 4.91e-06
===================================================================================
结果解释:当保持其他变量的取值不变时,男性买车的概率比女性高3.68%;当保持其他变量的取值不变时,年龄每增加一岁,买车的概率高2.62%。
(二)案例二
以titanic数据为例,演示逻辑回归的Statsmodels操作。数据链接:https://pan.baidu.com/s/1ipxk-hMWQasHefOX4mMC-w 提取码:07wv
首先导入相关库。
import pandas as pd
import numpy as np
import statsmodels.formula.api as smf
import statsmodels.api as sm
from patsy import dmatrices
用pandas的「read_csv」函数读取原始数据文件。
titanic = pd.read_csv(r'C:\Users\mi\Downloads\MLPython_Data\titanic.csv')
在Spyder的变量浏览器中,可查看titanic变量。
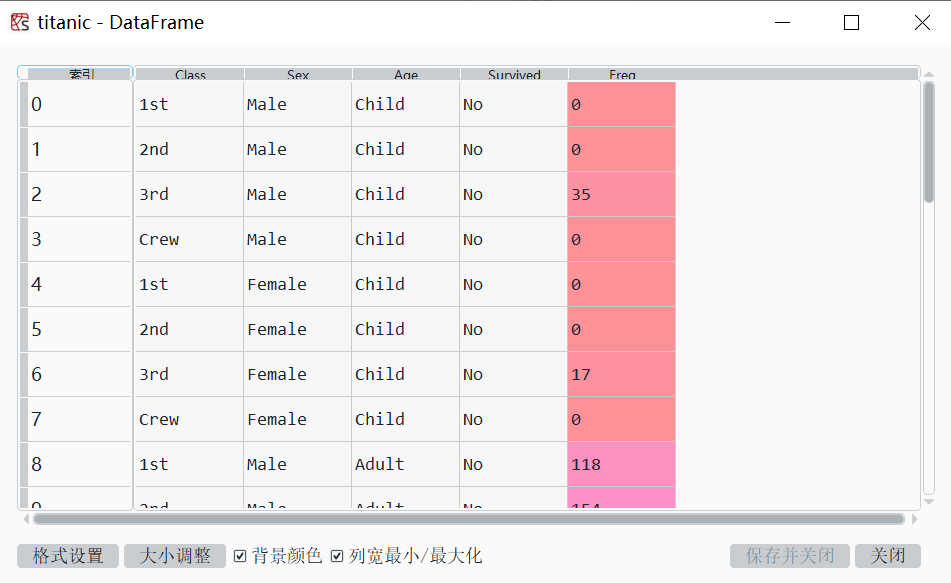
数据框的最后一个变量Freq,表示每个观测值在样本中出现的次数。因变量Survived取值为Yes或No,表示是否存活。因变量包括Age(取值为Child或Adult),Sex(取值为Male或Female),以及Class(取值为1st,2nd,3rd或Crew,分别表示头等舱、二等舱、三等舱与船员)。
需要将数据框完全展开,根据变量Freq让不同的观测值在数据框中以相应的频次出现。为此,使用to_numpy()方法,将变量Freq变为数组,并记为freq:
freq = titanic.Freq.to_numpy()
然后,使用np.repeat()函数,将np.arange(len(titanic))中每个元素,按照freq的频率进行重复,并记所得数组为index:
index = np.repeat(np.arange(len(titanic)),freq)
利用数据框的索引方法,可得整个样本:
titanic = titanic.iloc[index,:]
然后,去掉变量Freq:
titanic = titanic.drop('Freq',axis=1)
获取的titanic数据框如下:

可查看titanic数据框信息。
print(titanic.info())
结果为:
<class 'pandas.core.frame.DataFrame'>
Int64Index: 2201 entries, 2 to 31
Data columns (total 4 columns):# Column Non-Null Count Dtype
--- ------ -------------- ----- 0 Class 2201 non-null object1 Sex 2201 non-null object2 Age 2201 non-null object3 Survived 2201 non-null object
dtypes: object(4)
memory usage: 86.0+ KB
None
接下来进行Logit回归,有基于公式和基于数组两种方法。
「方法一:基于公式」
由于因变量survived是字符型的分类变量,如果不对survived做处理,则会报错。

image-20220822150240414
错误代码:
import statsmodels.formula.api as smflogit = smf.logit(formula='Survived ~ Class + Sex + Age', data = titanic)
results = logit.fit()
print(results.summary())
返回结果:
ValueError: endog has evaluated to an array with multiple columns that has shape (2201, 2). This occurs when the variable converted to endog is non-numeric (e.g., bool or str).
「回归时,若涉及虚拟变量,虚拟因变量必须是数值型的“虚拟变量”,而虚拟自变量可以是字符型的“分类变量”,也可以数值型的“虚拟变量”。」
本例中,自变量和因变量均是字符型的“分类变量”,因变量可以转变为数值型的“虚拟变量”,也可以不转变。
因此需要将代码修改为:
import statsmodels.formula.api as smftitanic['Survived'] = (titanic['Survived'] == 'Yes').astype(int) # False=0, True=1
logit = smf.logit(formula='Survived ~ Class + Sex + Age', data = titanic)
results = logit.fit()
print(results.summary())
「方法二:基于数组」
调用Logit() 函数的基本格式为:
sm.Logit(endog,exog)
本例中,自变量和因变量均是字符型的“分类变量”,可使用dmatrices()函数将字符型的“分类变量”统一转变为数字型的“虚拟变量”。
y,X = dmatrices('Survived ~ Class + Sex + Age',data = titanic,return_type='dataframe')
查看y、X数据框。
因变量y:包含两个虚拟变量,即”Survived[No]“和”Survived[Yes]“,而我们仅需要其中一个。为此,保留”Survived[Yes]“。
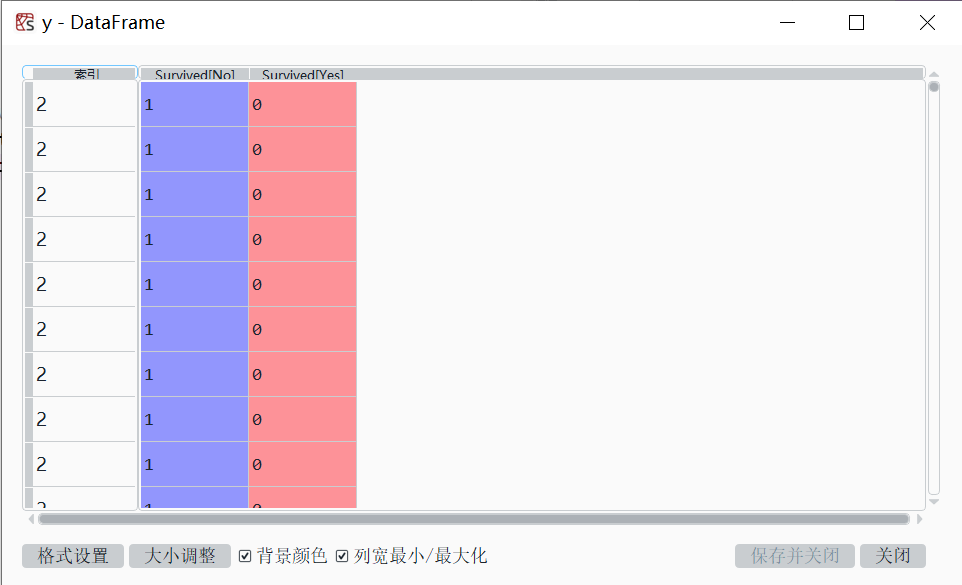
y= y.iloc[:,1]

自变量X:已根据原来的分类变量生成了相应的虚拟变量,并去掉了多余的参照类别。比如,对于分类变量Sex,去掉了Sex[T.Female],仅保留Sex[T.Male]。其中,'T.male'的前缀”T“表示”Treatment“。
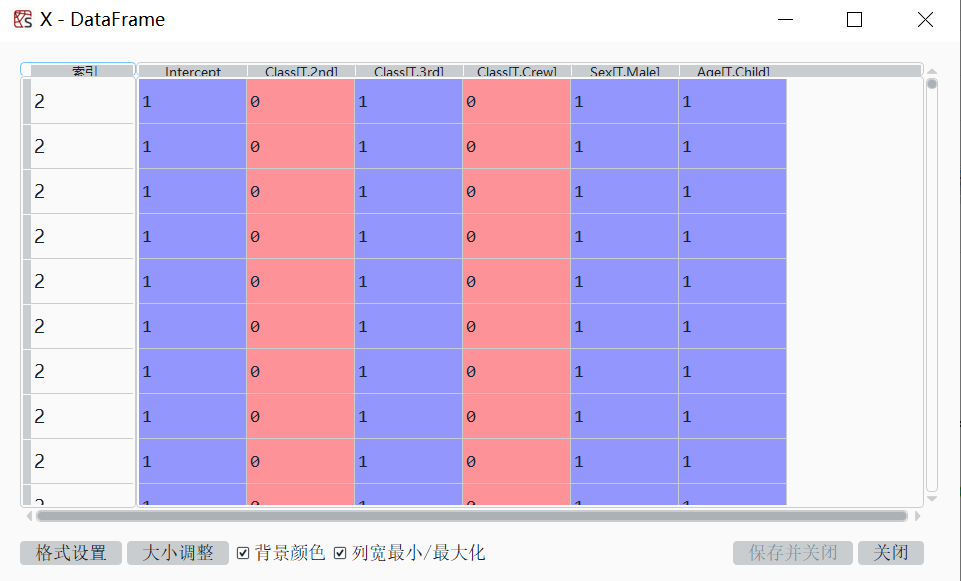
完整代码为:
import statsmodels.api as sm
from patsy import dmatricesy,X = dmatrices('Survived ~ Class + Sex + Age',data = titanic,return_type='dataframe')
y= y.iloc[:,1]logit = sm.Logit(y,X)
results = logit.fit()
print(results.summary())
方法一和方法二的结果一致,为:
Logit Regression Results
==============================================================================
Dep. Variable: Survived No. Observations: 2201
Model: Logit Df Residuals: 2195
Method: MLE Df Model: 5
Date: Mon, 22 Aug 2022 Pseudo R-squ.: 0.2020
Time: 15:06:41 Log-Likelihood: -1105.0
converged: True LL-Null: -1384.7
Covariance Type: nonrobust LLR p-value: 1.195e-118
=================================================================================coef std err z P>|z| [0.025 0.975]
---------------------------------------------------------------------------------
Intercept 2.0438 0.168 12.171 0.000 1.715 2.373
Class[T.2nd] -1.0181 0.196 -5.194 0.000 -1.402 -0.634
Class[T.3rd] -1.7778 0.172 -10.362 0.000 -2.114 -1.441
Class[T.Crew] -0.8577 0.157 -5.451 0.000 -1.166 -0.549
Sex[T.Male] -2.4201 0.140 -17.236 0.000 -2.695 -2.145
Age[T.Child] 1.0615 0.244 4.350 0.000 0.583 1.540
=================================================================================