第5章 实数域ℝ上的Fourier变换
The theory of Fourier series and integrals has always
had major difficulties and necessitated a large math-
ematical apparatus in dealing with questions of con-
vergence. It engendered the development of methods
of summation, although these did not lead to a com-
pletely satisfactory solution of the problem....For the
Fourier transform, the introduction of distributions
(hence the space S) is inevitable either in an explicit
or hidden form....As a result one may obtain all that
is desired from the point of view of the continuity and
inversion of the Fourier transform.
(Fourier级数和积分的理论一直存在重大困难,在处理收敛性问题时需要大型数学仪器。 它促成了求和方法的发展,尽管这些并没有导致产生完全令人满意的问题解......。对于Fourier变换,分布(因此空间 S )的引入是不可避免的,无论是显式还是隐式形式 ......。因此,从Fourier变换的连续性和逆变换的角度来看,人们可能会得到所有预期东西。)
-----------------------------------------------------------------------------------L. Schwartz, 1950
Fourier级数理论适用于圆周上的函数,或等价地适用于实数域 ℝ 上的周期函数。在本章中,我们为整个非周期性实数轴(real line)上的函数开发一个类似的理论。我们考虑的函数在无穷远处将适当地“小(small)”。有几种方法可以定义一个合适的“小(smallness)”的概念,但是,假设某种在无穷远处消失的“小”仍然是定义的关键。
在一方面,我们记得,周期函数的Fourier级数将一系列数(即Fourier系数)与该函数相关联; 在另一方面,给定一个 ℝ 上的合适函数 f ,与 f 关联的类比对象实际上是 ℝ 上的另一个函数 ,称其为 f 的Fourier变换。 由于 ℝ 上函数的Fourier变换又是 ℝ 上的函数,因此人们可以观察到函数及其Fourier变换之间的对称性,其类似对象在Fourier级数的设置中并不明显。
大致说来,Fourier变换是Fourier系数的连续版本。我们记得,定义在圆周上的函数 f 的Fourier系数 由
(1)
给出,则,在合适的意义上,我们有
(2) 。
此处,我们用 2πx 替换 θ ,和前我们经常按这样处理的方式一样。
现在,考虑以下类比,我们将所有离散符号(例如整数及其求和)替换为它们的连续对等对象(例如实数及其积分)。换句话说,给定一个实数域 ℝ 上的函数 f ,我们定义其 Fourier变换,将积分域从圆周上改变到所有整个实数域 ℝ ,在 (1) 中用 替换掉 n∈ℤ 。即,通过设置
(3) 。
我们进一步推进类比,考虑下面(2)的连续版本:用积分代替求和,用 替代
,导出了逆Fourier变换公式
(4) 。
在 上合适的假设之下,恒等式(4)事实上是成立的,本章理论的大部分旨在证明并探索这个关系。逆Fourier变换公式的有效性也通过下面的简单观察得到启发。假如
在一个包含于
有限区间上被支持,我们在
上以Fourier级数延拓
。则,令
趋近于无限,我们导出了(4) (见练习1).
Fourier 变换的特性使其成为研究偏微分方程的重要工具。例如,我们将会看到,逆Fourier变换公式是如何允许我们分析某些基于实数轴建模的方程。特别地,遵循圆周上发展起来的思想,我们解决了针对无限杆的时变(time-dependent)热传导方程和位于上半平面中的稳态热传导方程。
在本章的最后,我们讨论了与 Poisson 和公式
有关的更深入的主题,它给出了周期函数(和它们的Fourier级数)与线上的非周期函数(和它们的Fourier变换)之间的另一个显著联系。在前面的章节中,这个恒等式允许我们证明一个诊断,即,热传导核 满足好核的属性。此外,Poisson求和公式还出现在许多其它的设置中,特别是出现在数论部分,我们将在第2册书中看到这部分内容。
我们对我们选择的方案做出最后评述。在研究Fourier级数时,我们发现考虑圆周上的Riemann可积函数很有用。特别是,这种通用性向我们保证,即使是具有某些不连续性的函数也可以用该理论处理。相比之下,我们对Fourier变换基本属性的阐述是根据测试函数的 Schwartz[ʃwɔːts]( 1915年3月5日–2002年7月4日,法国数学家)空间 𝒮 来说明的。这些函数是无限可微的,并且与它们的导数一起在无穷大处迅速递减。对这个函数空间的依赖提供了一方法,允许我们快速得出主要结论,并以直接和透明的风格对结论进行公式化。 一旦执行此操作,我们将指出对某些更广泛设置的简易扩展。更通用的Fourier变换理论(必须以Lebesgue[ləbέ:g]( 1875年6月28日-1941年7月26日,法国数学家)积分为基础)将在第3册中讨论。
1. Fourier变换的基本理论(Elementary theory of the Fourier transform)
我们以扩展积分概念到定义于整个实数轴上的函数开始。
1.1 实数轴上的函数积分(Integration of functions on the real line)
已知封闭且有界区间上函数积分的概念,将这个定义扩展到实数域 ℝ 上的连续函数的最自然的定义便是
。
然,这个极限不存在。例如,假如 f (x) = 1 ,或者,甚至 f (x) = 1 / ( 1 + |x| ),则很显然,以上极限都是无穷的。片刻的思考表明,当| x |趋于无穷大时,如果我们对 f 施加足够大的下限,那么极限将存在。下面是一个有用的条件。
对于一个定义于实数域 ℝ 上的函数 f ,如果 f 是连续函数且存在一个常量 A > 0 ,使得对于所有 x∈ℝ ,都有
,
则称函数 f 是中速递降的(moderate decrease)。这个不等式指的是,函数 f 有界(比如,以 A 为界),此外,至少,在无穷远处它和 下降得同样快,因为
。
例如,对于函数 , 只要 n ≥ 2 ,则其便是中速递降的。另一个例子是函数
。
我们将用符号 ℳ(ℝ)来表示实数域 ℝ 上的中速递降函数集。作为一个练习,读者可以检验在通常的函数加和标题乘法则下,ℳ(ℝ)构成一个复数域 ℂ 上的向量空间。
接下来,我们可以看到,只要 f 属于 ℳ(ℝ) ,则,我们就可以定义
(5) ,
其中,现在这个极限是存在的。事实上,对于每一个 ,
是良好定义的,因为 f 是连续函数。现在,足以证明
是 Cauchy 序列,因为,假如
,则可以推出,当
时,
。
注意,我们也可以证明,当 时,
。在这一点上,我们注意到,我们可以将中速递降中定义的指数 2 用 1 + 𝜖 (𝜖 >0) 替换;即,对于所有 x∈ℝ ,有
。
这个定义同样契合于本章中发展的理论的目的。 我们选择 𝜖 = 1只是出于方便。
我们在一个命题中总结了实数域ℝ 上积分的一些基本属性。
命题1.1 按(5)定义的中速递降函数的积分满足下面的属性:
( ) 线性属性(Linearity): 假如 f ,g ∈ ℳ(ℝ) 且 a,b ∈ ℂ ,则
。
( ) 平移不变性(Translation invariance):对于每一个 h ∈ ℝ ,我们有
。
() 膨胀下的缩放(Scaling under dilations):假如 δ > 0 ,则
。
( ) 连续性(Continuity): 假如 f ∈ ℳ(ℝ) ,则,当 h ⟶ 0 时,
。
说一下关于证明的问题。属性(i)是显而易见的。为了验证属性(ii),只需考察当 时,
就足以证明,因为 。以上的差异主要在于,
对于任意大的 N , 当 N 趋近于无穷的时候,上式趋近于 0 。属性(iii)的证明再次类似,我们观察到, 。对于属性(iv),只需取 | h| ≤ 1 即可。对于一个预分配的 𝜖 > 0 , 我们首先选取任意大的 N ,使得
且
。
现在,使 N 固定,我们利用这个事实——因为 f 是连续的,因此,它在区间 [-N - 1, N + 1]上是一致连续的。因此,当 h ⟶ 0 时, 。因此,我们可以选取足够小的 h ,使得这个上确界小于 𝜖/4N 。综合在一起,则
,
因此,得出结论( iv )。
1.2 Fourier变换的定义(Definition of the Fourier transform)
假如 f ∈ ℳ(ℝ),对于 ξ∈ℝ ,我们定义 Fourier变换为
显然, ,因此,积分是中速递降的,因此,这个积分有意义。
事实上,最后一个观察意味着, 是有界的,此外,简单的论据证明,当
时,
是连续且趋近于 0 的(练习5)。然而,以上定义并不能确保
是中速递降的,或者,有一个具体的下降。特别是,在这个背景下,如何理解积分
及其导致的逆Fourier变换公式,是不明确的。为了弥补这一点不足,我们引入了由Schwartz考虑的更精确的函数空间,它在建立Fourier变换的初始属性的过程中非常有用。选择 Schwartz 空间的动机是源于将 f
![]() 的下降与 f 的连续性和可微性联系起来(反之亦然)的重要原则:
的下降与 f 的连续性和可微性联系起来(反之亦然)的重要原则: 随
下降得越快,则 f 一定“越平滑(smoother)”。反映这个原则的一个例子在练习3中给出。我们也注意到,
与
之间的这种关系相似于圆周上函数的平滑性与其 Fourier 系数的下降之间的关系;参见第2章推论2.4的讨论。
1.3 Schwartz空间(The Schwartz space)
实数域 ℝ 上的Schwartz 空间由所有无限可微的函数 f 的集合构成,且函数集 f 及其导数 在
(对于每一个 k, 𝓁 ≥ 0 )
的意义上,是寁降的(rapidly decreasing)(译注:寁(zǎn))。我们用 𝒮 = 𝒮(ℝ)表示这个空间,不过,读者应当验证 𝒮(ℝ) 是复数域 ℂ 上的向量空间。此外,假如 f ∈ 𝒮(ℝ) ,我们有
且
。
这表达了一个重要的事实——Schwartz 空间在多项式的微分和乘法下是封闭的。
一个Schwartz 空间中函数的简单例子是由
所定义的 Gauss 函数。它在Fourier变换理论及其它领域(如概率论和物理学)中起着核心的作用。读者可以验证, 的导数形如
, 其中,P(x) 是多项式,这立即证明了
。事实上,
属于 𝒮(ℝ) (只要 a > 0)。然后,我们将选取 a = π 来归一化 Gauss 函数。
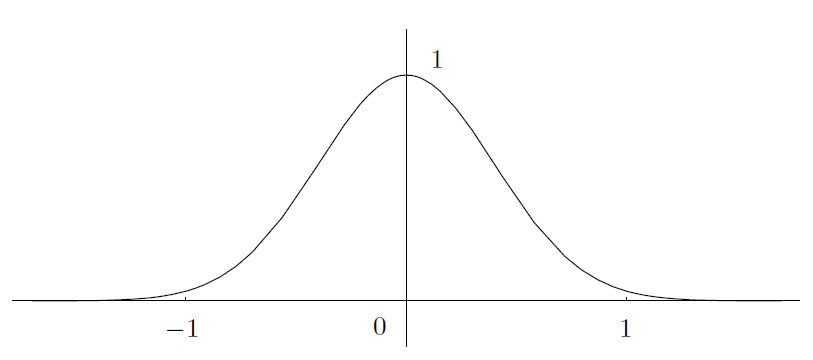
--------------------------------------------图1. Gauss 函数 ----------------------------------------------
𝒮(ℝ)中其它例子的一个重要分类是“隆凸函数(bump functions)或鼓凸函数”(译注:此函数的特征为中间有隆起的部分),它们在有界区间之外消失(练习4)。
作为最后的评述,请注意,尽管 在无穷远处也是寁降的,但是它在 0 点处是不可微的,因此,不属于𝒮(ℝ)。
1.4 𝒮 上的Fourier变换(The Fourier transform on 𝒮)
一个 f ∈ 𝒮(ℝ) 的 Fourier变换定义为
。
Fourier 变换的一些简单性质收集在以下命题中。我们使用记法
来表示—— 的Fourier变换是
。
命题 1.2 假如 , 则:
( )
(只要 h ∈ ℝ)
( )
(只要 h ∈ ℝ)
( )
(只要 h ∈ ℝ)
( )
。
特别是,除却 2πi 因子,Fourier变换按 x 交换微分和乘法。这是使得Fourier变换成为微分方程理论中核心对象的关键属性。我们后面会回到这一主题。
证明:
属性( i )是积分平移不变性的直接结果,属性( ii )可以从定义推出。此外,命题1.1 的第三个属性确立了属性( iii )。
由分部积分给出
,
因此,令 N 趋近于无穷即给出 ( iv )。
最后,证明属性 ( v ) ,我们必须证明, 是可微的,并求得其导数。令 𝜖 > 0 并考虑
。
因为 和
是寁降的,所以存在一个整数 N ,使得
且
。此外,对于
,存在
,使其意味着
,
因此,对于 ,我们有
定理 1.3 假如
, 则
。
该证明是对 Fourier 变换互换微分和乘法这一事实的简单应用。事实上,请注意到,假如 f ∈ 𝒮(ℝ) ,其Fourier变换 必定是有界的;此外,对于每一对非负整数 𝓁 和 k ,表达式
是有界的,因为,根据最后一个命题,它是
的Fourier变换。
逆Fourier变换公式
( 对 f ∈ 𝒮(ℝ) )
的证明,我们将在下一节中给出,是基于对函数 的存细研究之上,正好我们已经考察过一样,当 a > 0时,它属于 𝒮(ℝ) 。
1.4.1 Gauss函数作为好核(The Gaussians as good kernels)
我们以考察 a = π 这种情况开始,其归一化形式为:
(6)
为了理解为什么 (6) 式能成立,我们使用指数函数的乘法属性将积分简化为二维积分。更准确地说,我们可以按如下方式论证:
其中,我们使用了极坐标来计算二维积分。
Gauss函数的基本属性是我们的兴趣点,事实上,从(6)可以推出, 等于其Fourier变换。我们将这个重要的结果分离形成一个单独的定理。
定理1.4 假如 ,则
。
证明:
定义
,
并观察到,根据我们前面的计算, 。事实上,根据命题 1.2 中的属性(v),
,我们获得
。
根据以上同一命题的属性(iv) , 我们求得
。
假如我们定义 , 则从以上所见,可以推断出 ,
, 因此,G 是一个常量。因为 F ( 0 ) = 1 ,我们断定出 G 恒等于 1,因此,正如证明所示,
。
Fourier变换在扩张下的缩放特性产生了以下重要的变换定律,它来自命题 1.2 中的 (iii)(只是 δ 替换为 ) 。
推论1.5 假如 且
, 则
。
我们停下来,先做一个重要的观察。当 δ 趋近于0时,函数 在原点达峰值,而其 Fourier 变换
获得遍平状(flatter)。因此,在这个特别的例子中,我们看到
与
不能同时在原点局部化(localized)(即,聚焦(concentrated)))。这是一个泛化现象的例子,称为Heisenberg不确定原理(Heisenberg uncertainty principle),奖在本章末尾讨论。现在,我们以第2章中考虑的圆周上的好核族作为类比,基于实数轴构建一族好核族。事实上,关于
,
我们有:
( )
。
( )
。
( ) 对于每一个 η > 0 ,我们有
( 当 δ ⟶ 0 时) 。
为了证明(i),我们改变变量并利用(6),或者注意到,根据推率1.5,此积分等于 。
因此, ,很显然,属性 (ii) 也是成立的。最后,我们再次改变变量,得到
(当 δ⟶ 0 时) 。
因此,我们已经证明了下面的结论。
定理1.6 集合 是一个好核族 (当 δ⟶ 0 时)
接下来,我们经由卷积运算应用这些好核族。假如,f,g ∈ 𝒮(ℝ) ,则它们的卷积义为
( 7 ) 。
对于 x 的固定值,函数 f ( x - t)g( t )是按 t寁降的。因此,积分收敛。
按照第2章第4节的论据(稍加修改),我们得到下面的推论。
推论 1.7 假如 f ∈ 𝒮(ℝ),则
( 当 δ ⟶ 0 时, 按 x 一致性地)。
证明:
首先,我们声明, f 在ℝ上是一致连续的。事实上,任给一个 𝜖 > 0 ,存在一个 R > 0 ,使得,只要| x |≥R ,就有| f ( x )|< 𝜖 。此外,f 是连续的,因此,因此在压缩区间[-R, R]上一致连续。结合前面的观察,我们可以找到一个 η > 0 ,使得只要 | x - y |< η ,便有 | f ( x ) - f ( y ) | < 𝜖/4 。现在,我们像通常一样论证。使用好核的第一个属性,我们可以写成
,
且因为 ,我们求得
。
根据好核第三属性,第一个积分很小,事实上,f 是有界的,而第二个积分也很小,因为 f 是一致连续的且 。这就推出了引理。
1.5 逆Fourier变换(The Fourier inversion)
这下一个结论是一个恒等式,有时候称为乘法公式。
命题 1.8 假如 , 则
。
为了证明这个命题,我们需要离题简短地讨论一下针对双重积分的次序调换。假如
是平面 上的连续函数。我们将假设施加于 F 的如下下降条件:
。
则,我们可以指出,对于每一个固定的 x,函数 F(x,y) 以 y 中带递降,类似地,对于每一个固定的 y ,函数 F(x,y) 以 x 中带递降。此外,函数 是连续且递降的;类似地,
亦如此。最后,
。
这些事实的证明可以在附录中找到。
现在,我们应用这个事实到 。则,
和
,因此
,
这正是命题的论断。
乘法公式和 Gauss 函数的Fourier变换是其自身的事实,引导了第一主要定理的证明。
定理1.9 (逆Fourier变换) 假如 f ∈ 𝒮(ℝ),则
。
证明:
我们首先声明
。
令 使得
。根据乘法公式我们获得
。
因为 是一个好核,因此,第一个积分当 δ 趋近于 0 时去到 f (0)。因为第二个积分当 δ 趋近于 0 时,很显然收敛于
, 声明得证。一般地,令
使得
。
正如定理 1.9 的名称所表明的那样,它提供了一个公式,可以逆向 Fourier 变换;事实上,我们看到,Fourier 变换除却 x 到 –x 的变化,是其自身的逆变换。更确切地说,我们可以定义两个映射: 和
分别为如下形式
和
。
因此,是 ℱ Fourier 变换,定理 1.9 确保在 𝒮(ℝ)上 , 其中,
是恒等映射(译注:符号“○”表示复合函数)。此外,由于 ℱ 与
的定义差异仅在于指数中的符号,我们发现
, 因此,我们也有
。作为结论,我们推断出
是 𝒮(ℝ)上Fourier变换的逆向变换,因此我们有下面的结论。
推论 1.10 Schwarts 空间上的 Fourier 变换是一个双向的映射(bijective)。
1.6 Plancherel公式(The Plancherel formula)
关于Schwartz函数卷积,我们需要稍微深入一点的结论。关键事实在于,Fourier变换交换卷积与逐点乘积。这是一个可类比于针对Fourier级数的情景。
命题1.11 假如 f , g∈ 𝒮(ℝ), 则
( )
。
( )
。
( )
。
证明:
为了证明 f * g 是寁降的,首先观察到,对于任意 𝓁 ≥ 0 ,我们有 ,
使得对于每一个 ,
是有界函数。这种估算结转(carry over)到卷积
的转数,从而(thereby)证明了
。因为
(对 k = 1,2,....) 。
首先,对于 k = 1 这种情况,在 f * g 的定义之下对其进行微分即可证明恒等式。在这种情况下,通过 dg/dx 的寁降可证微分和积分的交换的合理性。然后,对于每一个k , 根据迭代性,可以推出恒等式。
对于固定的 ,变量
的替换证明
。
这个变量替换是两个变量替换的组合,y ⟼ – y 和 y ⟼ y – h (且 h = x )。对于第一个变量替换,我们使用这个观察结果,即,对任意 Schwartz 函数 F, ;对于第二个变量替换,应用命题 1.1 的第 (ii) 项即可。
最后,考虑 。因为 f 和 g 是寁降的,分别考虑 | x | ≤ 2| y | 和 | x | ≥ 2| y | 这两种情况,我们看到,命题 1.8 之后关于积分次序变化的讨论适用于 F 。在这种情况下,
和
。因此,
, 这就意味着(iii),因此,命题得证。
现在,我们使用 Schwartz 函数卷积属性来证明本节的主要结论。我们想到的结论是 ℝ 上 Parseval 恒等式对 Fourier 级数的函数模拟(analogue)。
Schwartz 空间可以使用 Hermit 内积
来配备,与内积关联的范数(norm)(译注:“norm”本意指“木工为了获得直角而使用的带直角的工具”,这样做是为了达到某种实用的标准,或者模式。此处的“范数”,即“规范数”的简称,实为度量长度、大小等的概念)为
。
理论中第二个主要定理指出,Fourier变换是 𝒮(ℝ) 上的单式变换(unitary transformation)。
定理1.12(Plancherel 定理) 假如 , 则
。
证明:
假如 ,定义
。 则
。现在,令
。很显然,我们有
和
。
现在,这个定理可以从应用逆向公式并令 x = 0 推出,即
。
1.7 (几个结论)向中速递降函数的扩展(Extension to functions of moderate decrease)
在前面的章节中,我们将Fourier变换和Plancherel公式限定于函数归属于Schwartz空间的这种情况。一旦我们做出附加的假设,即考虑之下的函数的Fourier变换也是中速递降的,则将这些结果扩展到中速递降函数只是水到渠成的事。事实上,关键的观察,即两个中速递降的函数 f 和 g 的卷积 f * g 也是一个中速递降函数(练习7),这很容易获证;另有 。此外,乘法公式对中速递降函数依然成立,由此,我们推断出当 f 和 g 均是中速递降函数的时候的逆Fourier变换公式和Plancherel公式。
这种公式的泛化,虽然在适用范围上趋于保守,但在某些场景下还是挺有用的。
1.8 Weierstrass[váiəʃtrà:s]逼近定理(The Weierstrass approximation theorem)
现在,我们暂且离题,通过进一步地探调我们的好核来证明Weierstrass定理。这个结论我们曾经在第2章中略有提及。
定理1.13 令 f 为闭合且有界区间 [a,b]⊂ℝ 上的连续函数。则,对于任意 𝜖 > 0 ,都存在一个多项式 P 使得
。
换句话说,f 可由多项式 P 一致地逼近。
证明:
令 [-M,M ] 表示在其内部包含闭区间[a,b]的任意闭区间,并令 g 为实数域 ℝ 上的连续函数,且其值在闭区间 [-M,M ]之外等于0,而在[a,b]之内等于 f 。例如,如下扩展 f :通过从 f (b) 到 0 的直线段定义从 b 到 M,且通过从 f (a) 到 0 的直线段定义从 a 到 – M 的函数 g 。令 B 为 g 的边界,即,对于所有的 x,有| g(x)|≤ B 。则,因为 是一个好核族,g 是连续且具备紧致支持的(compact support),我们可以像推论1.7 的证明那样论证,可以看到,当 δ 趋近于无穷大时,
一致收敛于 g 。 事实上,我们选取
使得对于所有的 x∈ℝ ,有
。
现在,我们记得通过幂级数扩展 给出的
,此级数在 ℝ 的每一个紧致区间上都是一致收敛的。因此,存在一个 N 使得
( 对于所有
),
其中, 。我们记得,g 消失于闭区间 [-M,M] 之外, 则,对于所有 x ∈ [-M,M ],我们有
因此,这个三角不等式意味着,只要 x ∈ [-M , M ] ,就有 ,因此,当 x ∈ [a, b] 时,
。
最后,注意,g * R 是一个以 x 作为自变量的多项式。事实上,根据定义, ,且 R ( x –t ) 以 x 作为自变量的多项式,因为,它在几次扩展之后,可以表达为
,其中,其具有有限和。这样就推出了定理的证明。
2. 一些偏微分方程的应用(Applications to some partial differential equations)
我们之前提到过,Fourier变换的一个重要特性是它可以通过多项式交换微分和乘法。 我们现在将这个关键事实与逆Fourier变换定理一起用于求解一些特定的偏微分方程。
2.1 实数轴上的时变热传导方程(The time-dependent heat equation on the real line)
在第4章中,我们考虑了圆周上的热传导方程。在这里,我们研究实数轴上的类似问题。
考虑一根无限长的杆,我们将其作为实数轴模型。并假设给到我们一个杆上位于 t = 0 时刻的初始温度分布函数 f (x)。现在,我们想确定位于点 x 处且时间 t > 0 的温度 u ( x ,t )。类似于第1章中给出的考量证明,当合适地归一化 u 的时候,它可以解下面的微分方程
(8) ,
此方程称为热传导方程(heat equation)。我们施加的初始条件是 。
正如圆周上的情况一下,这个解是以卷积的形式给出的。事实上,按
且
对方程(8)按 x 变量(通常)进行Fourier变换导出
。
固定 ξ , 则这是一个以 t 为自变量的普通微分方程(且未知 , 因此,存在一个常量 A( ξ ),使得
。
我们也可以取初始条件的Fourier变换,并求得 , 因此,
。这就导出了下面的定理。
定理 2.1 假如(given) f ∈ 𝒮(ℝ),令
,
其中, 是热传导核。则:
() 当 x ∈ ℝ 且 t > 0 时,函数 u 是
,且作为热传导方程的解。
() 当 t ⟶ 0 时, u(x ,t) ⟶ f (x)(按 x 一致地),因此,假如我们设 u(x ,0) = f (x),则 u 在上半平面
的闭包(closure)上是连续的。
() 当 t ⟶ 0 时,
。
证明:
因为 , 以 x 为自变量进行Fourier变换,得到
, 因此,
。逆Fourier变换公式给出
。
按照积分符号下的微分,读者可验证(i) 。事实上,读者可观察到,u 是无限可微的。注意,(ii)是推论 1.7 的直接结论,最后,根据 Plancherel 公式,我们有
。
为了理解当 t ⟶ 0 时最后一个积分趋近于 0 ,我们按如下论证:
因为 且 f ∈ 𝒮(ℝ),我们可以找到一个 N 使得
,
且对于任意小的 t ,因为 有界,我们有
。
因此,对于任意小的 t , 。这就完成了对定理的证明。
以上定理确保了具有初始数据 f 的热传导方程的解的存在。假如唯一性被恰当地归一化,则这个解也是唯一的。在这方面,我们注意到, 满足下面的附加属性。
推论 2.2 函数 在对于任意 T > 0 ,
(9) ( 对于每一个k ,𝓁 ≥ 0)
的意义上,按 t 一致性地归属于 𝒮(ℝ) 。
证明:
这个结论是按如下过程估算的结果:
。
事实上,因为 f 是寁降的,当 | y|≤ | x|/2 时,我们有 。此外,假如
, 则
,我们获得了以上的不等式。因此,我们发现,当 0 < t < T 时,u (x , t )是一致寁降的。
同样的结论也可以按 x 变量适用于 u 的导数,因为我们可以在积分符号下微分,并用 f ‘ 替换 f 并应用上面的估算结论,等等。
以上结论导出了下面的唯一性定理。
定理 2.3 假如 u (x , t)满足下面的条件:
(i) u 在上半平面的闭包中是连续的。
(ii) u 满足 t > 0 的热传导方程。
(iii) u 满足边界条件 u (x , 0) = 0 。
(iv) u 满足边界条件 u (x , 0) = 0 。
u (. ,t ) ∈ 𝒮(ℝ) 是按 t 一致性的,犹如在(9)中的情况一样。
则,我们推出 u = 0 。
以下,我们使用缩略形式 和
分别表示
和
。
证明:
我们将方程解 u (x , t ) 在时刻 t 的能量定义为
。
显然,E ( t ) ≥ 0 。因为 E ( t ) = 0 就足以证明 u 是一个递降函数,并且是通过证明 dE /dt ≤ 0 来完成的。这种施加于 u 上的假设允许我们在积分符号下微分 E ( t ),即,
。
但 u 满足热传导方程,因此, 且
,于是,在分部积分之后(其中,我们使用了这个事实—— u 及其以 x 为自变量的导数随着 |x|⟶ ∞ 而寁降),我们求得
正如所声明的那样。因为,对于所有的 t 有 E (t) = 0 ,因此 u = 0 。
另一个热传导方程的唯一性定理(比(9)具有更少的限制性假设)可见问题 6。唯一性不成立的例子可见练习12和问题4。
2.2 在上半平面上的稳态热传导方程(The steady-state heat equation in the upper half-plane)
我们现在关注的是位于上半平面 中的方程
(10) 。
我们所要求的边界条件是 u ( x ,0) = f ( x )。运算符号 Δ 是 Laplace 算子,且以上偏微分方程方程表述了 面上受边界条件 u = f 约束的稳态热传导方程。对于上半平面而言,解这个问题的核称为Poisson 核,且由下式给出
(其中,x ∈ ℝ 且 y > 0) 。
这与在第2章的第5.4节中讨论的圆盘的Poisson核类似。
注意,对于每一个固定的 y ,Poisson核 作为 x 的函数仅仅是中速递降的,因此,我们将使用适用于这些类型的函数的Fourier变换理论(见1.7见)。 我们按照在时变热传导方程中的情况一样推进,通过按 x 变量对等式(10)(按常规)进行Fourier变换,从而获得
,
其具有边界条件, 。这个以 y 为自变量(固定 ξ )的常微分方程的通解采用形式
。
假如我们忽略第二项(因为其寁降性),在设置 y = 0 之后,我们求得
。
因此,按 f 与 Fourier 变换为 的核的卷积给出 u。这正是上面给出的 Poisson核,正如下面所证明的那样。
引理 2.4 下面两个恒等式成立:
,
。
第一个公式非常直接,因为我们可以将积分拆分为从-∞到 0,和从 0 到 ∞ 两部分。则,因为 y > 0 ,我们有
,
类似地,有
。
因此,
。
现在,第二个公式是逆Fourier 变换定理应用于 和
都是中速递降的这种情况的结果。
引理 2.5 当 y ⟶ 0 时,Poisson核在实数域 ℝ 上是好核。
证明:
在引理的第二个公式中设 ξ = 0,则表明 ,并且,显然
,因此,余下验证好核的最后一个属性。给定一个固定的 δ > 0,我们可以做变量替换 u = x/y 使得
,
当 y ⟶ 0 时,这个量去到 0 。因为 是一个偶函数,证明完结。
下面的定理确保了我们问题的解的存在性。
定理 2.6 假如 , 令
。则:
(i) 在上半平面
上是
且
。
(ii) 当 y ⟶ 0 时,u(x ,y) ⟶ f ( x ) 是一致性地 。
(iii) 当 y ⟶ 0 时, 。
(iv) 假如 u(x ,0) = f ( x ),则 u 在上半平面的 闭包中是连续的,且在
u(x ,y) ⟶ 0 (当 | x | + y ⟶ ∞时)
的意义上消失于无穷远处。
证明:
(i), (ii),和 (iii) 部分的证明与热传导方程的证明类似,留予读者去完成。对于(iv)部分,只要 f 是中速递降的,则其就是两个简单估算的结果。首先,下面的不等式
可按这样的方式证明(与热传导方程的情况一样)——将积分 拆分成 | t | ≤ | x |/2 和 | t | ≥ | x |/2 两部分。因此,由于
,我们有
。
当| x| ≥ | y |时,使用第一个估算,而当 | x| ≤ | y |时,使用第二个估算,这样就给到了无穷远处期望的递降。
下面证明这个解在本质上是唯一的。
定理 2.7 假如 u 在上半平面的 闭包中是连续的,且满足,对于
有
以及 u(x ,y)消失于无穷远处。则 u = 0 。
一个简单的例子证明,关注 u 在无穷远处的下降条件是必要的:取 u(x ,y) = y 。很显然,u 满足稳态热传导方程且在实数轴上消失,且 u 并不恒等于 0。
这个定理的证明依赖一个关于谐函数(满足 Δu = 0 的函数)的事实。这个事实是,谐函数在某一点的值等于其围绕以该点为圆心的任何圆的平均值。
引理 2.8(均值属性(Mean-value property)) 假如 Ω 是 上的一个开集,令 u 为
类的一个函数,且在 Ω 中 Δu = 0 。假如,以(x , y)为圆心的圆盘的闭包和半径 R 的闭包包含于 Ω ,则,对于任意 0 ≤ x ≤ R,有
。
证明:
令 。按极坐标表达 Laplace 算子,方程 Δu = 0 意味着
。
假如我们定义 , 则上式给出
。
在圆上的积分由于
是周期函数而消失,因此,
,则
一定是常量。在 r = 0 处计算这个表达式,我们求得
。因此,F 是一个常量,但因为 F(0) = u(x ,y),我们最后求得对于任意 0 ≤ x ≤ R 有 F(r) = u(x ,y),这便是均值属性。
最后,注意以上的论据隐含在第2章定理5.7的证明过程中。
我们采用反证明证明定理 2.7。分别考虑 u 的实部和虚部,我们可以假设 u 其自身是实数,并且在某处严格为正值,比如,对于某个 且
有
。我们将看到,这将会推导出矛盾。首先,因为 u 在无穷远处消失。我们可以找到一个半径为 R 的任意大半圆盘
, 且在半圆盘之外
。接下来,因为 u 在
上是连续的,它在上面可以获得它的最大值 M,因此,存在一个点
,其值为
,而在半圆盘上,u(x ,y) ≤ M ;此外,由于在半圆盘之外
。现在,谐函数的均值属性意味着,只要积分圆位于上半平面,就有
,
矛盾的事实在于 。现在令
,并再次使用 u 的连续性,我们看到,这意味着
。这个矛盾的事实在于,对于所有 x ,u(x ,0) = 0 。
3. Poisson[pwasɔ:ŋ]求和公式 (The Poisson summation formula)
Fourier变换的定义是出于对Fourier级数连续版本的需求,适用于定义在实数轴上的函数。我们现在证明,圆周上的函数分析与实数域 ℝ 上的相关函数之间存在更显著的联系。
已知一个实数轴上的函数 f ∈ 𝒮(ℝ) ,我们可以通过技巧(recipe)构造另一个新的函数
。
因为 f 是寁降的,其级数在每一个 ℝ 的紧致子集上是绝对且一致收敛的,因此, 是连续的。注意,
,因为,在以上求和中,从 n 到 n + 1 的逾越(passage)仅仅平移了由
定义的级数项。因此,函数
是以 1 为周期的。因此,函数
称为函数 f 的周期化(periodization)。
有另一种方式可以实现函数 f 的“周期化版本(periodic version)”,即,通过 Fourier分析。以恒等式
开始,考虑其离散相似对象(analogue), 只不过积分由求和公式
所替代。再一次地,其和绝对且一致地收敛,由于 属于 Schwartz 空间,因此
连续,最后导出了同样的函数。
定理3.1 (Poisson summation formula)( Poisson求和公式) 假如 f ∈ 𝒮(ℝ) ,则
。
特别地,令 x = 0 ,我们有
。
换句话说,f 的周期化的Fourier系数由 f 在整数上的Fourier变换值精确地给出。
证明:
为了验证第一个公式,采用第2章中的定理2.1就已足够证明两侧(都是连续的)具有相同的 Fourier 系数(视为圆周上的函数)。很显然,右侧的第 m 项 Fourier 系数是 。对于左侧,我们有
其中,交换积分与求和是允许的,因为 f 是寁降的。这就完成了定理的证明。
我们注意到,当我们仅仅假设 和
都是中速递降函数时,这个定理也可扩展到这种情况。事实上,对这个扩展应用的证明不变。
已经证明,周期化运算在许多问题上是重要的,甚至当 Poisson求和公式都不适用的场合。我们举 1 例,考虑初等函数 f (x) = 1/ x (x ≠ 0)。结果是,当对称求和的时候, 给出了余切函数的部分分数的分解。事实上,当 x 不是整数的时候,这个和等于 π cot (πx) 。类似地,对于
, 我们得到,只要 x ∉ ℤ,就有
(见练习15)。
3.1 𝜗 函数和ζ函数(Theta and zeta functions)
定义 s > 0 时的 𝜗 函数(译注:𝜗 为希腊字母 θ 的数学体)为
。
施加于 s 上的限制条件使得级数绝对收敛。这个特殊函数的关键事实在于,它满足下面的函数方程。
定理3.2 只要 s > 0 ,就有 。
定理的证明通过将Poisson求和公式简单地应用于函数对
和
来实现。
当 Re{ s }> 0 时,𝜗 函数也可以推展到 s 取复数值的情况,并且函数方程在这时仍然是有效的。𝜗 函数与数论中的另一个重要的函数 ζ 函数(译注:ζ 为希腊字母 ζ 的数学体)具有紧密联系,对于 Re{ s } > 1 的 ζ 函数定义为
。
后面我们将会看到,这个函数携带了素数(prime number)的基本信息(见第8章)。
业已证明,ζ ,𝜗 和另一个重要函数通过下列恒等式关联起来:
,
其对于 s > 1 是有效的(见练习17和18)。(译注:𝜏 的数学体LaTex语法 \mathit{\tau})
回到函数 𝜗 ,定义其广义形式 Θ(z|𝜏)为
,
其中,Re{ 𝜏 }> 0 且 𝜏∈ℂ 。取 z = 0 且 𝜏 = is ,我们得到 Θ(z|𝜏) = 𝜗(s) 。
3.2 热传导核(Heat kernels)
与 Poisson 求和公式和 𝜗 函数相关的另一个应用是圆周上的时变热传导方程。这个受条件 u( x,0) = f ( x )(其中,f 是以 1 为周期的周期函数)约束的方程
的解,已在前面章节由公式
给出,其中, 是圆周上的热传导核,即,
。
特别注意我们在上一节中对广义 𝜗 函数的定义,我们有 。此外,我们记得实数域 ℝ 上的热传导方程,它产生了热传核
,
其中, 。 这两个对象之间的基本关系是Poisson 求和公式的直接结果。
定理 3.3 圆周上的热传导核是实数轴上的热传导核的周期化:
。
尽管证明 在实数域 ℝ 上是好核非常简单,但我们又面对更困难的问题,即,证明
在圆周上也是好核。上面的结论允许我们解决这个问题。
推论3.4 核 在 t ⟶ 0 的情况下是好核。
证明:
我们已经观察到, 。现在,注意到,由于
,从以上公式立即可推出
。最后,我们声明,当 | x | ≤ 1/2 时,
,
其中,误差(error)满足 且
。为了理解这一点,再次注意,定理中的公式给出
;
因此,由于 | x | ≤ 1/2 ,
。
现在注意,只要 , 就有
和
,因此,
。因此
。
这个声明的证明完成,且结论为,当 t ⟶ 0 时, 。现在,很清楚了,当
满足当 t ⟶ 0 时,
,
因为 是如此。
3.3 Poisson核(Heat kernels)
按上面关于热核的讨论类似的方式,我们指出圆盘的Poisson核与上半平面之间的关系,其中
和
。
定理3.5 (其中,
) 。
这又是一个Poisson求和公式应用于 和
的直接推论。
当然,在这里,我们是在假设 和
是中速递降的前提下使用Poisson求和公式。
4. Heisenberg[háizənbɛək]不确定性原理(The Heisenberg uncertainty principle)
该原理的数学要旨(thrust)可以根据函数与其Fourier变换之间的关系来表述。这个基本的底层法则,以其最隐晦(vaguest)和最通用(general)的形式表明,函数及其Fourier变换不能同时完全(essentially)是局部化的。更准确地说,如果一个函数的质量(mass)的“多数(preponderance)”集中在一个长度为 L 的区间内,那么它的Fourier变换的质量的多数不可能位于一个完全(essentially)小于 的区间内。准确的表述如下。
定理 4.1 假如 ψ 是一个位于 𝒮(ℝ) 上的函数,且满足归一化的条件 。则
,
并且,当且仅当 ( 其中,
且
) 时,等号成立。事实上,对于每一个
,我们有
。
证明:
第二个不等式实际上由第一个不等式通过用 替换 ψ(x)再变更变量而推导出。为了证明第一个不等式,我们按如下论证。从我们的归一化假设
开始,并记得 ψ 和 ψ’ 是寁降的,通过分部积分给出一个积分式
。
最后一个恒等式沿袭,因为 。因此,
,
其中,我们已经使用了 Cauchy-Schwarz不等式。根据Fourier变换的属性,恒等式
成立,而Plancherel公式推导出了定理中不等式的证明。
如果等式成立,那么我们在应用 Cauchy-Schwarz 不等式的地方也一定有等式,因此,对某些常量,我们求得 。这个方程的解是
,其中,A 是常量。因为,我们希望 ψ 是 Schwartz 函数,所以我们必须取 β = -2B < 0 ,且因为我们施加了限制条件
,我们求得
,正如所证明的那样。
定理 4.1 中包含的精确论断首先在量子力学(quantum mechanics)研究中被发现。当人们考虑可以同时定位粒子的位置和动量(momentum)的程度时,它就出现了。假设我们正在处理(比方说)沿实数轴行进的电子,那么根据物理定律,物质受“状态函数(state function)” ψ 的支配,我们可以假设它在 𝒮(ℝ) 中,并且根据以下要求
(11)
归一化。然后确定粒子的位置,而不是一个确定的点 x ;相反,它的可能位置由如下的量子力学规则给出:
粒子位于区间(a,b)的概率是 根据这个原则,在 ψ 的辅助下,我们可以计算出粒子可能的位置:事实上,粒子可能仅有很小的可能性位于已知的区间(a’, b’)中,但无论如何,它一定在实数轴上的某个地方,因为
。
除了概率密度(probability density) 之外,还存在粒子可能所处的期望值(expectation)。期望值是对粒子所处位置的最佳猜测。由
所确定的概率分布给出,是由
(12)
所定义的量。为什么期望值是我们的最佳的猜测呢?考虑更简单的(理想化的)情景,在这个情况中,给予我们的粒子仅在实数轴上的有限多个不同的点 处可以发现,且粒子在
点出现的概率为
, 而
。则,如果我们不知道额外信息的情况下,我们被迫对粒子的位置做出一个选择,很自然地,我们会取
,这就是粒子可能位置的恰当的加权平均值。显然,量(12)是这种情况的通用(积分)版本。
接下来,我们来到方差(variance)的概念。在我们的术语中,它是附加到我们的期望上的不确定性(uncertainty)。已经确定了粒子的预期位置是 x![]() (由(12)给出)。其结果的不确定性是量
(由(12)给出)。其结果的不确定性是量
(13) 。
注意,假如 ψ 高度地集中于 附近,则意味着存在 x 在
附近的一个高概率,因此(13) 很小,因为对积分的大部分贡献发生在
附近的 x 值上。这里,我们有很小的不确定性。在另一方面,假如 ψ(x)是相当扁平的(即,概率分布
不是很集中),则积分(13)相当大,因为
的大值将生效,因此,不确定性相对较大。
也值得观察,期望值 是一种其不确定性
是最小的一种选择。事实上,假如我们试图将其针对
的导数等于 0 来最小化这个量,我们求得
,这就给到 (12) 。
到目前为止,我们已经讨论了与粒子位置相关的“期望”和“不确定性”,同样相关的是关于其动量的相应概念。量子力学(对动量)的相应规则是:
属于区间(a,b)的粒子的动量 ξ 的概率是 ,其中,
是
的Fourier变换。
将这两个定律与定理 4.1 结合得出
作为粒子位置不确定性和动量不确定性乘积的下界。因此,我们对粒子的位置越确定,我们对它的动量就越不确定,反之亦然。但是,我们通过重新缩放以更改测量单位来简化这两个定律的表述。实际上,引入了一个基础的但很小的称为 Planck 常数和物理数 𝒽。如果考虑得当,物理结论是
(位置的不确定性)×(动量的不确定性) 。
内容来源:
<<Fourier Analysis: An Introduction>> E.M. Stein & R. Shakarchi