红黑树,是一种二叉搜索树,但在每个结点上增加一个存储位表示结点的颜色,可以是Red或
Black。 通过对任何一条从根到叶子的路径上各个结点着色方式的限制,红黑树确保没有一条路
径会比其他路径长出俩倍,因而是接近平衡的。
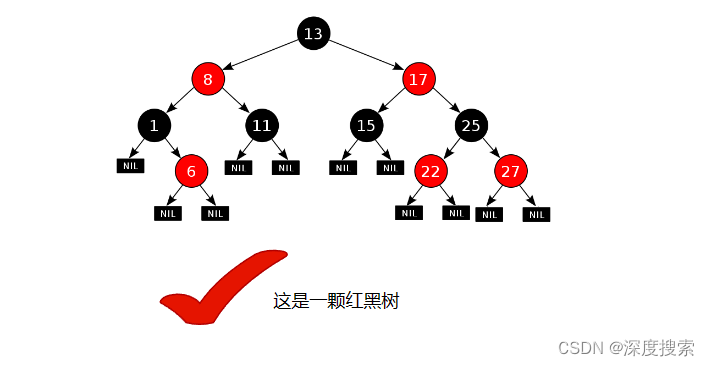
红黑树的性质
最长路径不超过最短路径的2倍
满足以下条件:
1. 每个结点不是红色就是黑色
2. 根节点是黑色的
3. 如果一个节点是红色的,则它的两个孩子结点是黑色的
4. 对于每个结点,从该结点到其所有后代叶结点的简单路径上,均 包含相同数目的黑色结点
5. 每个叶子结点都是黑色的(此处的叶子结点指的是空结点)
- 不能有连续的红结点
- 所有路径的黑结点个数相同
- 根是黑结点
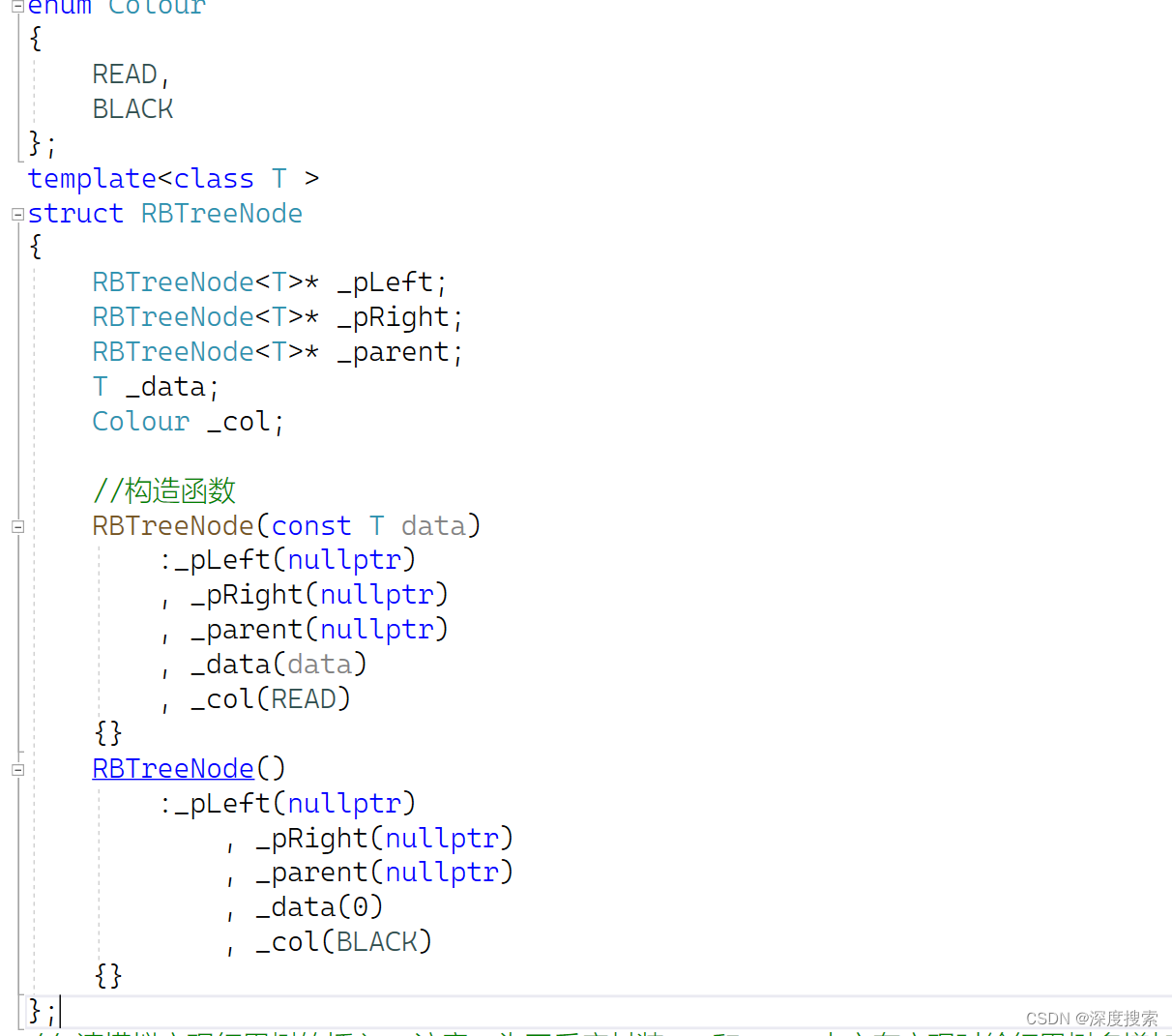
结点定义
红黑树是一个三叉链模型,成员变量包括左右孩子,父亲结点,当前颜色,Value
成员函数有构造函数
为什么对于一个结点,默认设为红色?
如果是新增为黑色结点,会导致左右的黑色结点数变化,不满足个路径的黑色结点数相同。因此需要大量调整。(必须调整)
如果处理为红色,只有当父亲也会红的情况下才需要调整。(非必要调整)
所有将新结点默认为红色就是为了减少调整的次数
结点的插入
红黑树的插入主要有以下几个步骤
- 一开始为空树,new新结点
- 不为空,查找合适的插入点(小就往左,大就往右)
- 提前保存父亲结点,双向链接新结点
- 调整:
- 如果父亲也是红,则需要进行调整
颜色的调整
如果父亲是红,就有连续的俩个红色结点,进行调整
调整的话要根据父亲在左边还是右边 ,分成俩大类讨论
首先看父亲在左边
约定:cur为当前节点,p为父节点,g为祖父节点,u为叔叔节点
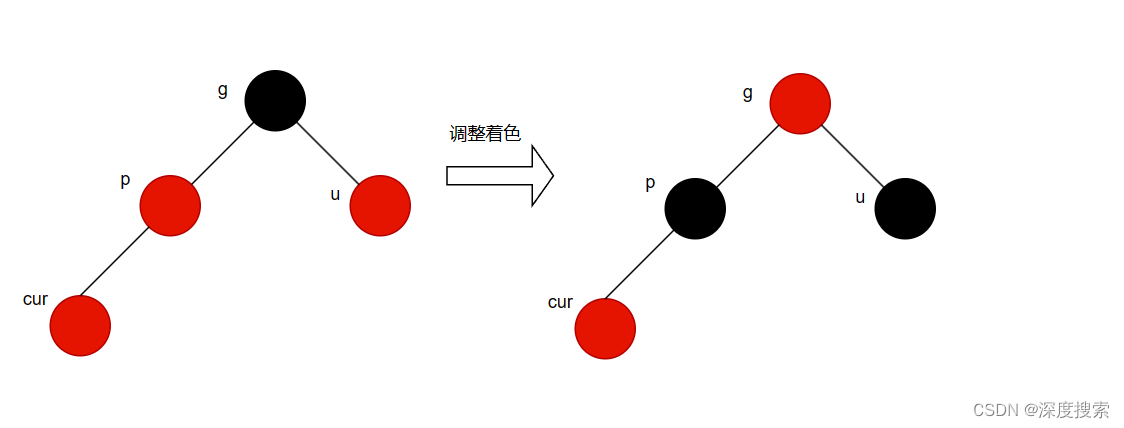
情况一、叔叔存在且为红
这个情况完整来说就是祖父是黑,父亲和叔叔必定是红,cur是红
调整思路:父亲和叔叔着色为黑,祖父着色为红,继续向上调整
因为cur和父亲的颜色为红,那么祖父的颜色是必为黑,则从祖父开始到根,每条路径的黑色结点为数目为 2(空为黑+祖父是黑),那么将父亲和叔叔修改为黑 ,祖父的结点改为红,则不会影响整条路径的黑色结点数目,调整祖父的结点颜色为红,则会影响影响祖父的父亲。(如果祖父的父亲为红,就存在俩个连续的红,继续调整)
情况二、叔叔存在且为黑或者叔叔不存在
调整思路
1)如果是直线型,即父亲在左,cur也在左
调整方法:
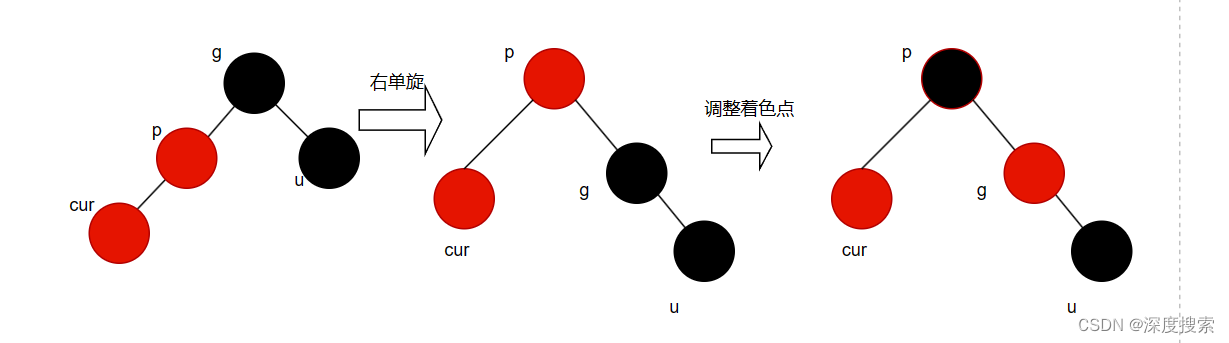
对祖父结点进行右单旋,将p的结点变红,祖父的结点变红
要保证右边的路径黑色结点数目不变,同时左边的红色结点数减少,就要将左边的树旋转到右边,然后进行着色。
由于着色不对uncle结点进行,所以叔叔结点存在与否不做要求。
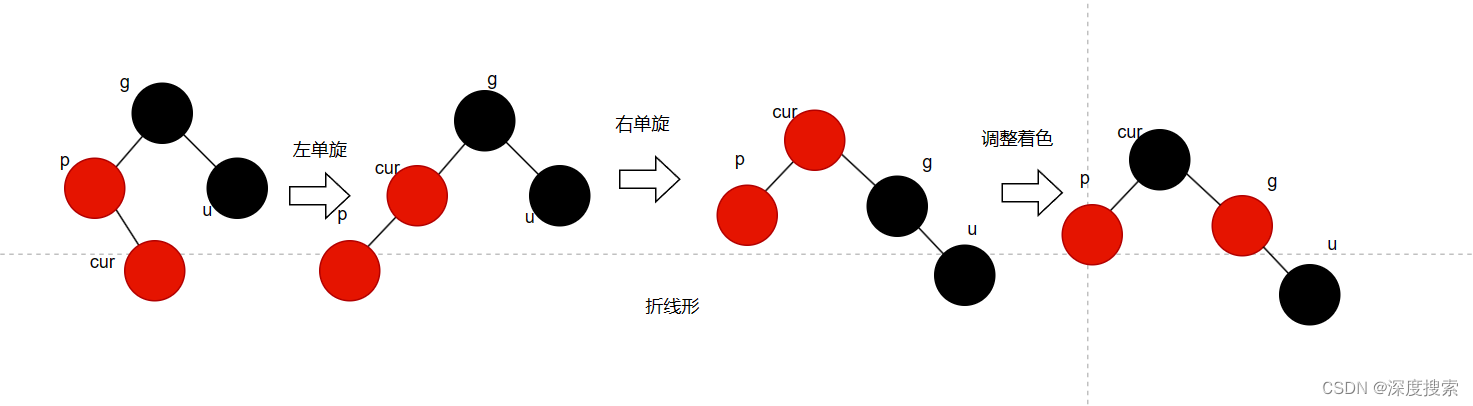
2)如果是折线形,先对父亲结点进行左单旋,调整为2)的形状,再右单旋,调整颜色。
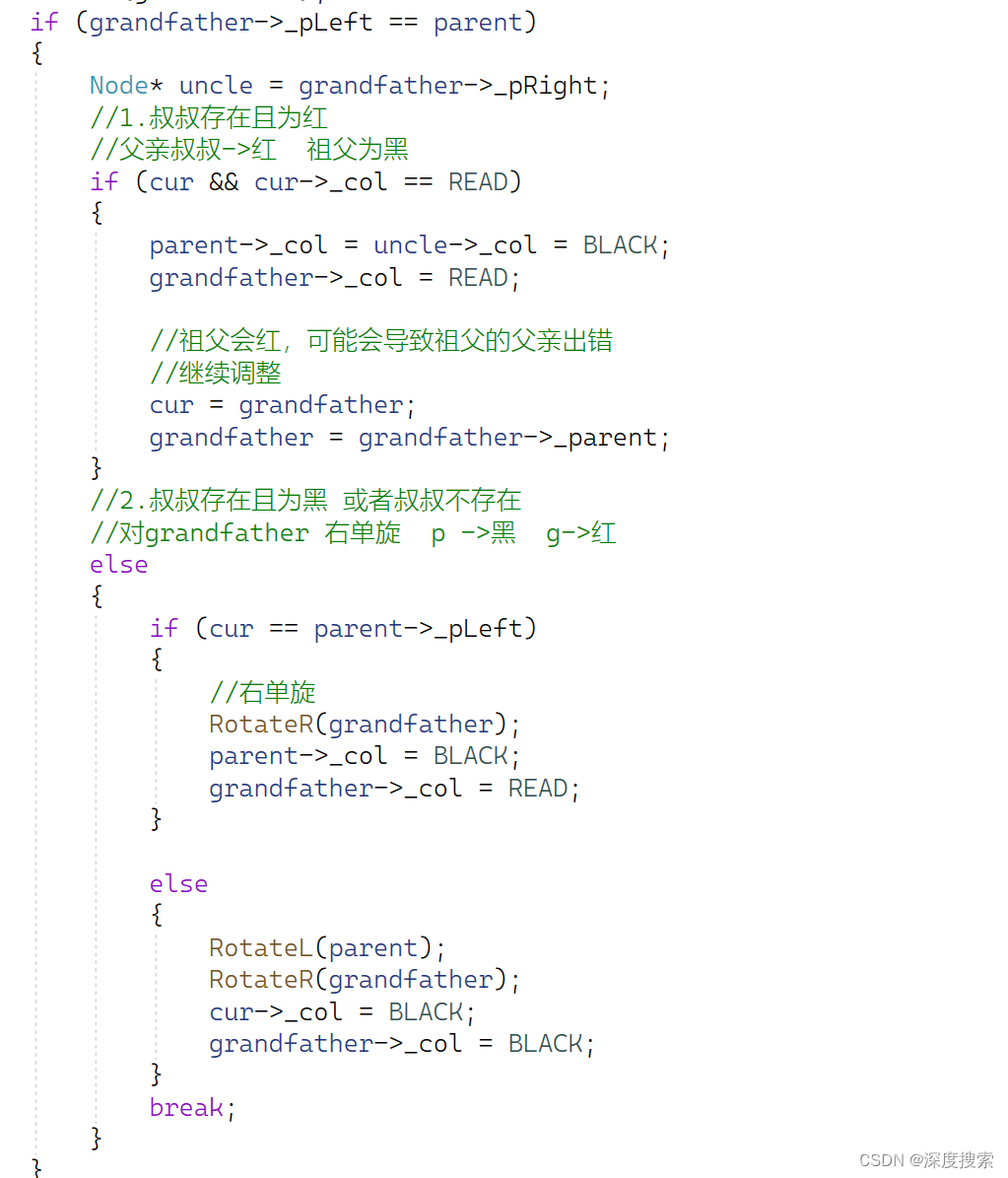
第二类:
父亲在右边
这一类的方式与父亲在左边基本一致,这里简单说明
1)叔叔存在且为红,父亲叔叔变黑,祖父为红,继续向上调整
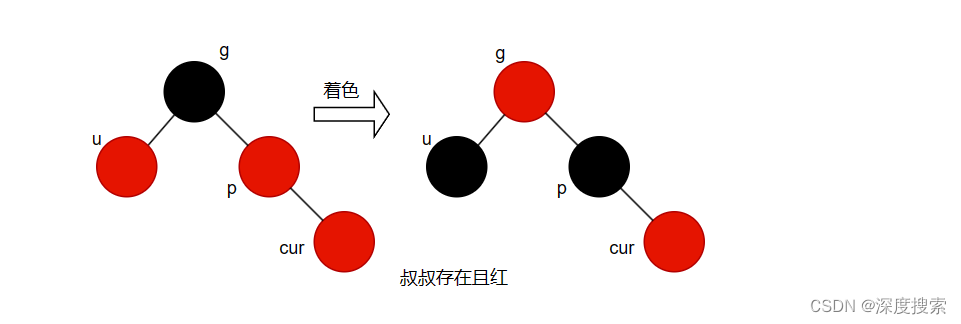
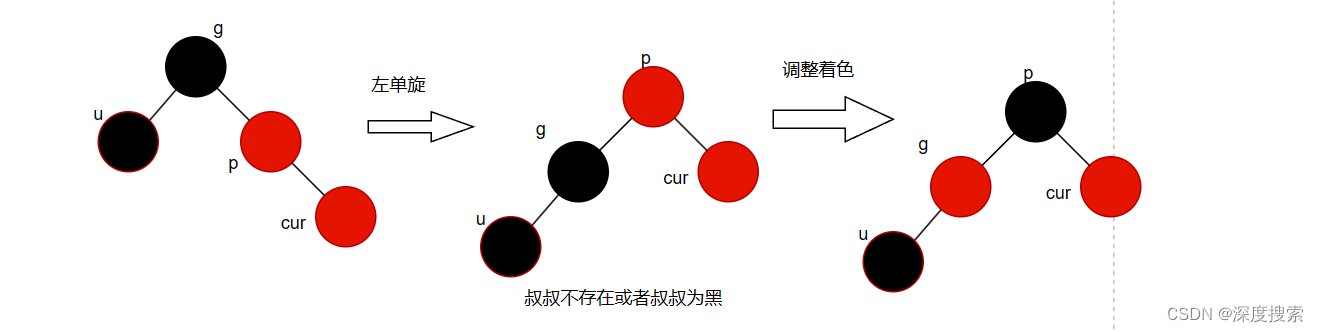
2)直线型 叔叔存在且为黑或者叔叔不存在。
3)折线形
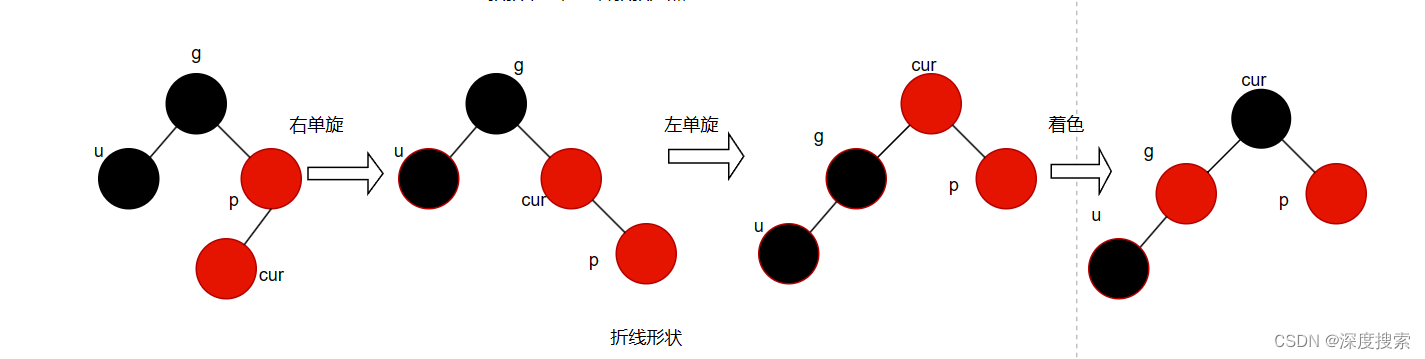

最后一步将根结点暴力调整为黑色
红黑树的验证
1)空树也是红黑树
2)任意一条路径的黑色结点个数都相同
先求出一条路径的黑色结点,再用递归去比较其它的路径
3)不能有连续的红色结点。判断cur和父亲的颜色

关于红黑树的左旋和右旋,可以参考文章:【C++】AVL树-CSDN博客
红黑树的性能
主要对比于AVL树,AVL树相较红黑树更加平衡,建立树的高度比较矮,查找的速度会更快
当时AVL树要进行大量的旋转,会极大消耗时间和空间。而在增删中红黑树性能有优势,相对于实现,红黑树较AVL树简单,因为在实际运用中红黑树更多
点我gitee:红黑树的实现代码