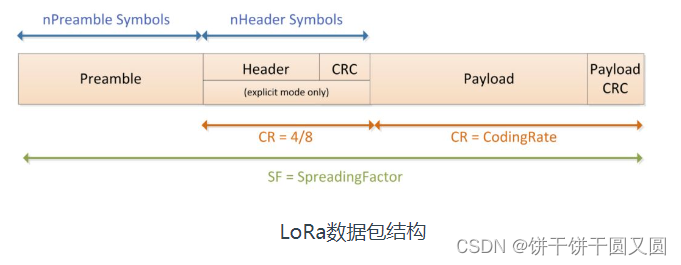
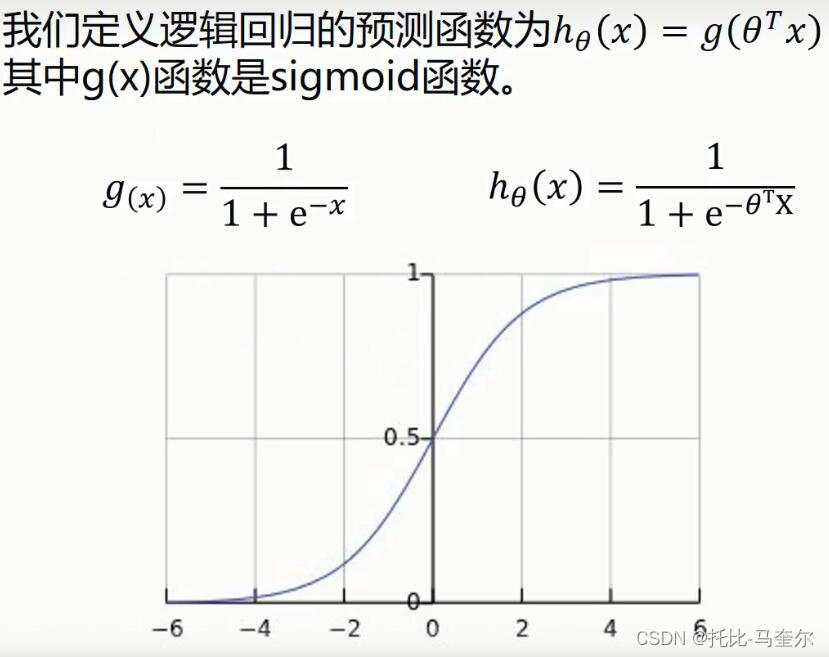
Sigmoid函数
逻辑回归的预测函数

梯度下降法-逻辑回归
import matplotlib.pyplot as plt
import numpy as np
# 生成一个关于分类器性能的详细报告。
# 这个报告包含了每个类别的精度、召回率、F1分数,以及所有类别的平均精度、召回率和F1分数
from sklearn.metrics import classification_report
# 用于数据预处理的,比如标准化、归一化、正则化
from sklearn import preprocessing
# 数据是否需要标准化
scale = False# 载入数据
data = np.genfromtxt("LR-testSet.csv", delimiter=",")
x_data = data[:,:-1]
y_data = data[:,-1]def plot():x0 = []x1 = []y0 = []y1 = []# 切分不同类别的数据for i in range(len(x_data)):if y_data[i]==0:x0.append(x_data[i,0])y0.append(x_data[i,1])else:x1.append(x_data[i,0])y1.append(x_data[i,1])# 画图scatter0 = plt.scatter(x0, y0, c='b', marker='o')scatter1 = plt.scatter(x1, y1, c='r', marker='x')# 画图例plt.legend(handles=[scatter0,scatter1],labels=['label0','label1'],loc='best')plot()
plt.show()给样本添加配置项
# 数据处理,添加偏置项
x_data = data[:,:-1]
y_data = data[:,-1,np.newaxis]print(np.mat(x_data).shape)
print(np.mat(y_data).shape)
# 给样本添加偏置项
X_data = np.concatenate((np.ones((100,1)),x_data),axis=1)
print(X_data.shape)逻辑回归的激活函数
def sigmoid(x):return 1.0/(1+np.exp(-x))
逻辑回归的代价函数
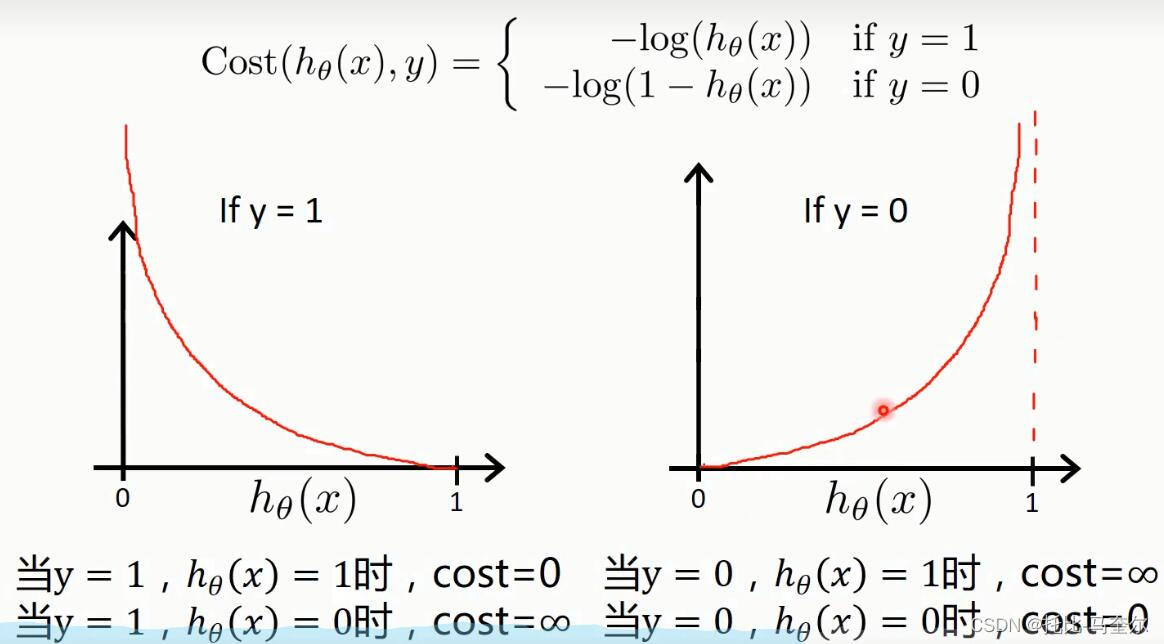
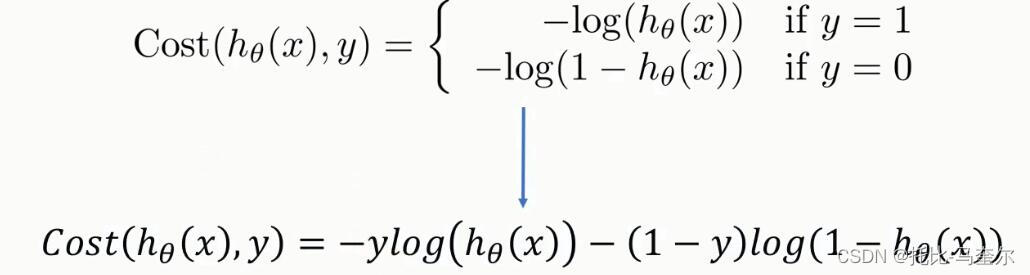
def cost(xMat, yMat, ws):# 这种乘法是按照位置相乘,对应位置直接乘# sigmoid(xMat*ws)指的就是预测值left = np.multiply(yMat, np.log(sigmoid(xMat*ws)))right = np.multiply(1-yMat, np.log(1 - sigmoid(xMat*ws)))# 返回的是逻辑回归的代价函数return np.sum(left + right) / -(len(xMat))
代价函数求偏导,但是要记得是以e为底,不是以10为底

梯度下降算法
def gradAscent(xArr, yArr):if scale == True:xArr = preprocessing.scale(xArr)xMat = np.mat(xArr)yMat = np.mat(yArr)lr = 0.001epochs = 10000costList = []# 计算数据行列数# 行代表数据个数,列代表权值个数m,n = np.shape(xMat)# 初始化权值ws = np.mat(np.ones((n,1)))for i in range(epochs+1):# xMat和weights矩阵相乘h = sigmoid(xMat*ws)# 计算误差# 因为100行三列没法进行运算,所以需要进行转置,而且由于是矩阵,最后的乘积就是最后相加之后得值ws_grad = xMat.T*(h - yMat)/mws = ws -lr*ws_gradif i % 50 == 0:# 每迭代五十次,就保存一下值costList.append(cost(xMat,yMat,ws))return ws,costList测试集
if scale == False:# 画图决策边界plot()# 以下的内容就是画边界线的x_test = [[-4],[3]]# sigmoid函数0左边和右边是进行分类的# w0+x1w1+x2w2 这个方程就是相当于sigmoid函数中g(θT*x)中的θT*xy_test = (-ws[0] - x_test*ws[1])/ws[2]plt.plot(x_test, y_test, 'k')plt.show()loss值的变化
x = np.linspace(0,10000,201)
plt.plot(x, costList, c='r')
plt.title('Train')
plt.xlabel('Epochs')
plt.ylabel('Cost')
plt.show()sklearn-逻辑回归
import matplotlib.pyplot as plt
import numpy as np
from sklearn.metrics import classification_report
from sklearn import linear_model
from sklearn import preprocessing
# 数据是否需要标准化
scale = False# 载入数据
data = np.genfromtxt("LR-testSet.csv", delimiter=",")
x_data = data[:,:-1]
y_data = data[:,-1]def plot():x0 = []x1 = []y0 = []y1 = []# 切分不同类别的数据for i in range(len(x_data)):if y_data[i]==0:x0.append(x_data[i,0])y0.append(x_data[i,1])else:x1.append(x_data[i,0])y1.append(x_data[i,1])# 画图scatter0 = plt.scatter(x0, y0, c='b', marker='o')scatter1 = plt.scatter(x1, y1, c='r', marker='x')# 画图例plt.legend(handles=[scatter0,scatter1],labels=['label0','label1'],loc='best')plot()
plt.show()构建并拟合模型
logistic = linear_model.LogisticRegression()
logistic.fit(x_data, y_data)测试集
if scale == False:# 画图决策边界plot()# 以下的内容就是画边界线的x_test = np.array([[-4],[3]])# intercept_代表模型的偏置 coef_[0][0]代表模型的权值y_test = (-logistic.intercept_ - x_test*logistic.coef_[0][0])/logistic.coef_[0][1]plt.plot(x_test, y_test, 'k')plt.show()梯度下降法-非线性逻辑回归
import matplotlib.pyplot as plt
import numpy as np
from sklearn.metrics import classification_report
from sklearn.preprocessing import PolynomialFeatures
from sklearn import preprocessing
# 数据是否需要标准化
scale = False# 载入数据
data = np.genfromtxt("LR-testSet2.txt", delimiter=",")
x_data = data[:,:-1]
y_data = data[:,-1,np.newaxis]def plot():x0 = []x1 = []y0 = []y1 = []# 切分不同类别的数据for i in range(len(x_data)):if y_data[i]==0:x0.append(x_data[i,0])y0.append(x_data[i,1])else:x1.append(x_data[i,0])y1.append(x_data[i,1])# 画图scatter0 = plt.scatter(x0, y0, c='b', marker='o')scatter1 = plt.scatter(x1, y1, c='r', marker='x')# 画图例plt.legend(handles=[scatter0,scatter1],labels=['label0','label1'],loc='best')plot()
plt.show()定义多项式回归
# 定义多项式回归,degree的值可以调节多项式的特征
poly_reg = PolynomialFeatures(degree=3)
# 特征处理
x_poly = poly_reg.fit_transform(x_data)
# fit():首先,它使用输入的x_data来“训练”或“适应”模型
# transform(x_data):然后,它使用已经训练好的模型来转换输入的数据。# 在这种情况下,它将把x_data中的每个特征转化为多项式特征。结果会是一个新的数据集,其中包含了原始数据的所有多项式特征degree的数字越大,模型的拟合程度越好。但是也要保证不要过拟合
def sigmoid(x):return 1.0/(1+np.exp(-x))def cost(xMat, yMat, ws):left = np.multiply(yMat, np.log(sigmoid(xMat*ws)))right = np.multiply(1 - yMat, np.log(1 - sigmoid(xMat*ws)))return np.sum(left + right) / -(len(xMat))def gradAscent(xArr, yArr):if scale == True:xArr = preprocessing.scale(xArr)xMat = np.mat(xArr)yMat = np.mat(yArr)lr = 0.03epochs = 50000costList = []# 计算数据列数,有几列就有几个权值m,n = np.shape(xMat)# 初始化权值ws = np.mat(np.ones((n,1)))for i in range(epochs+1):# xMat和weights矩阵相乘h = sigmoid(xMat*ws)# 计算误差ws_grad = xMat.T*(h - yMat) / mws = ws - lr*ws_gradif i % 50 == 0:costList.append(cost(xMat,yMat,ws))return ws,costListravel()函数
[[1,1],[2,2]]
# ravel之后变为一维
[1,1,2,2]生成等高线图
# 获取数据值所在的范围
x_min, x_max = x_data[:, 0].min() - 1, x_data[:, 0].max() + 1
y_min, y_max = x_data[:, 1].min() - 1, x_data[:, 1].max() + 1# 生成网格矩阵
# 步长是0.02
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02),np.arange(y_min, y_max, 0.02))# np.r_按row来组合array
# np.c_按colunm来组合array
# >>> a = np.array([1,2,3])
# >>> b = np.array([5,2,5])
# >>> np.r_[a,b]
# array([1, 2, 3, 5, 2, 5])
# >>> np.c_[a,b]
# array([[1, 5],
# [2, 2],
# [3, 5]])
# >>> np.c_[a,[0,0,0],b]
# array([[1, 0, 5],
# [2, 0, 2],
# [3, 0, 5]])# dot表示向量的内积,即对应位置元素相乘相加
z = sigmoid(poly_reg.fit_transform(np.c_[xx.ravel(), yy.ravel()]).dot(np.array(ws)))
# ravel与flatten类似,多维数据转一维。flatten不会改变原始数据,ravel会改变原始数据
# sigmoid函数可以将任何实数映射到介于0和1之间的值
for i in range(len(z)):if z[i] > 0.5:z[i] = 1else:z[i] = 0# 将我们修改后的z重新塑形为与xx相同的形状。这意味着我们原先的一维数组z现在变成了二维数组,形状与xx和yy相同
z = z.reshape(xx.shape)# 等高线图
cs = plt.contourf(xx, yy, z)
plot()
plt.show()sklearn-非线性逻辑回归
import numpy as np
import matplotlib.pyplot as plt
from sklearn import linear_model
from sklearn.datasets import make_gaussian_quantiles
from sklearn.preprocessing import PolynomialFeatures生成数据
# 生成2维正态分布,生成的数据按分位数分为两类,500个样本,2个样本特征
# 可以生成两类或多类数据
# 该函数由 sklearn.datasets 提供,用于生成高斯分布的样本数据。这个函数可以产生指定数量(n_samples)的样本,
# 每个样本都有指定数量(n_features)的特征,并且每个特征都服从高斯分布(正态分布)。n_classes 参数指定了生成的样本应属于的类别数量
x_data, y_data = make_gaussian_quantiles(n_samples=500, n_features=2,n_classes=2)plt.scatter(x_data[:, 0], x_data[:, 1], c=y_data)
plt.show()创建并拟合模型
logistic = linear_model.LogisticRegression()
logistic.fit(x_data, y_data)# 获取数据值所在的范围
x_min, x_max = x_data[:, 0].min() - 1, x_data[:, 0].max() + 1
y_min, y_max = x_data[:, 1].min() - 1, x_data[:, 1].max() + 1# 生成网格矩阵
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02),np.arange(y_min, y_max, 0.02))z = logistic.predict(np.c_[xx.ravel(), yy.ravel()])# ravel与flatten类似,多维数据转一维。flatten不会改变原始数据,ravel会改变原始数据
z = z.reshape(xx.shape)
# 等高线图
cs = plt.contourf(xx, yy, z)
# 样本散点图
plt.scatter(x_data[:, 0], x_data[:, 1], c=y_data)
plt.show()# 使用逻辑回归模型来对给定的数据集进行预测,并计算模型的准确率得分
print('score:',logistic.score(x_data,y_data))此时生成的模型进行逻辑回归的准确率太低,需要再次定义逻辑回归模型
# 定义多项式回归,degree的值可以调节多项式的特征
poly_reg = PolynomialFeatures(degree=5)
# 特征处理
x_poly = poly_reg.fit_transform(x_data)
# 定义逻辑回归模型
logistic = linear_model.LogisticRegression()
# 训练模型
logistic.fit(x_poly, y_data)# 获取数据值所在的范围
x_min, x_max = x_data[:, 0].min() - 1, x_data[:, 0].max() + 1
y_min, y_max = x_data[:, 1].min() - 1, x_data[:, 1].max() + 1# 生成网格矩阵
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02),np.arange(y_min, y_max, 0.02))z = logistic.predict(poly_reg.fit_transform(np.c_[xx.ravel(), yy.ravel()]))# ravel与flatten类似,多维数据转一维。flatten不会改变原始数据,ravel会改变原始数据
z = z.reshape(xx.shape)
# 等高线图
cs = plt.contourf(xx, yy, z)
# 样本散点图
plt.scatter(x_data[:, 0], x_data[:, 1], c=y_data)
plt.show()print('score:',logistic.score(x_poly,y_data))非凸函数和凸函数
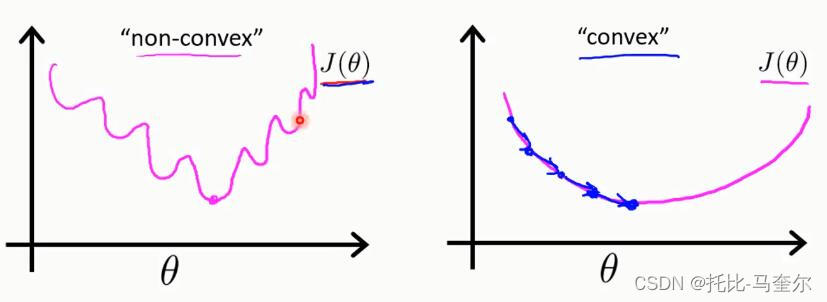
线性回归的代价函数是凸函数
逻辑回归正则化

正确率与召回率
正确率与召回率是广泛应用于信息检索和统计学分类领域的两个度量值,用来评价结果的质量
一般来说,正确率就是检索出来的条目有多少是正确的,召回率就是所有正确的条目有多少被检索出来了
F1值=2*(正确率*召回率)/ (正确率+召回率),用于综合反映整体的指标。
这几个指标的取值都在0-1之间,数值越接近1,效果越好