回溯法
回溯法=深度优先+剪枝,实质就是用递归代替for循环。
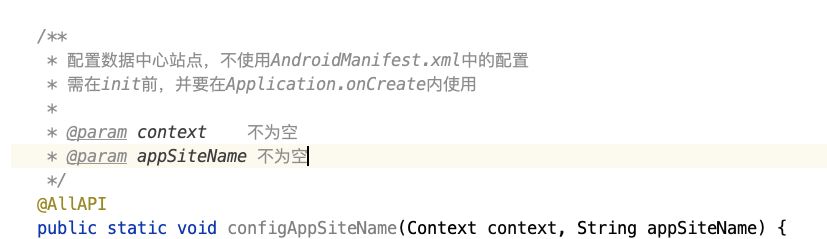
仍然是一种暴力遍历的手段,通常与递归配合使用,用于解决单纯for循环无法处理的问题,比如组合、切割、子集、排列等问题——比如求n个数里的长度为k的组合,需要k重循环,回溯使用递归代替一重循环,以此实现遍历。
使用代码对回溯法进行举例说明,也是回溯法的模板:
void backtracking(参数){
if(终止条件){叶子节点收集结果;
return ;}
for(集合元素集){
处理节点;
递归;
回溯操作;//执行到此步说明此次循环递归已经找到一个结果,//需要回溯来找新的结果
return;}
}
组合
n个数找长度为k的所有组合,需要嵌套k个循环,回溯法通过递归控制循环层数,每层递归一个for循环,举例代码如下:
二维数组result用于保存结果
一维数组path用于记录组合
void backtracking(n,k,startindex){//n个数,k长度,当前起始位置index
if(path.size==k){//叶子节点,找到结果
result.push(path);
return;}
for(int i=startindex;i<=n;i++){
path.push(i);//装入一个元素
backtracking(n,k,i+1);//递归得到一个结果
path.pop();//弹出元素,进行回溯
N 皇后
nn的棋盘上放n个皇后,不能同行同列或处于对角线上,问有多少种摆法,将回溯法表示为树便于观察:
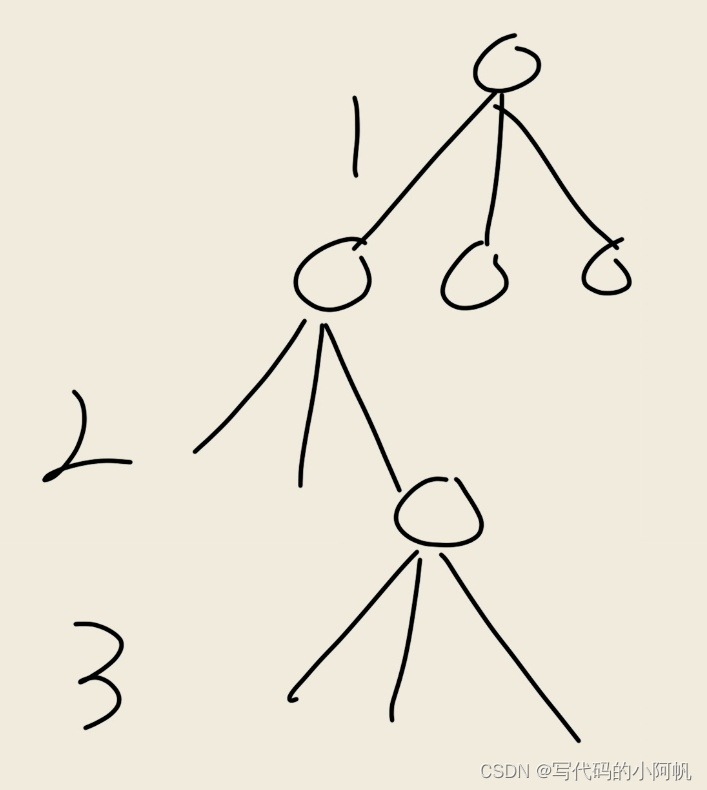
解释:将棋盘按行遍历,先在第一行的第i列放置皇后,再在放了第一个皇后的基础上在第二行放皇后,如此遍历。(示例是33的棋盘,该情况下皇后问题无解)。该树的深度为n。
先将该想法实现为代码如下:
设置三维数组result用于存储结果;
void backtarcking(chessboard,n,row){//n*n的棋盘,当前放置位置为第row行
if(row==n){//说明到了叶子节点,保存结果
result.pushback(chessboard);
return ;}
for(int i=0;i<n;i++){
if(isvalid(row,i,chessboard,n)//判断当前位置能否放置皇后,代码简单,略
{
chessboard[row][i]="Q";
backtrack(chessboard,n,row+1)//继续算法进行下一行的放置
chessboard[row][i]=" ";//一轮放置已完成,放置初始化进行下一轮//回溯,恢复原有,继续遍历
回溯法总结
代码其实都不难,判断结束条件并记录结果,for循环,内部处理节点,递归,回溯操作;说白了就是确定终止条件+单层递归逻辑两步,主要是用递归代替循环,尝试然后初始化(回溯)的思想。
涉及的难点和体现代码质量的地方就在于剪枝,在for循环内免去不必要的计算和判断可以大幅提高运行性能,这是需要多加考虑的点。
贪心算法
大题思路就是阶段性的局部最优=>整体最优,多数情况下无法严谨证明,题目一般也没啥规律和框架,多思考把握实践,运行结果正确就行,不用太钻牛角尖。
喂饼干问题
胃口和饼干两个数组,饼干大于胃口才能喂饱,问能喂饱多少小孩,策略是 用大饼干喂胃口大的孩子(局部最优)就能喂饱最多小孩(整体最优)。
直接代码展示:
//胃口g 1,2,7,10
//饼干s 1,3,5,9
sort(g);sort(s)//把饼干和胃口数组先从小到大排序,便于比较
int result=0;
int index=s.size()-1;
for(i=g.size()-1;i>=0;i--){
while(index>=0&&s[index]>=g[i]){//使用while便于控制条件,//饼干大于胃口成功投喂,判断index需大于0
result++;
index--;
}}
return result
饼干注意
循环不可颠倒,现在是由大饼干找小孩,吃一个换个饼干,如果由小孩找饼干,吃不上换个饼干,可能正好比上最大的,白循环了。
此外:用小饼干匹配小胃口也是可以。
划分字母区间
分割字符串区间使区间内的字符只出现在该区间内。例如:
s=ababcdacadefegde;//一个区间为ababcdaca,另一个为defegde,//第一个区间包含所有abc,第二个包含所有defg//输出[9,7]
思路为1,记录字符出现的最远位置,2,根据最远位置划分划分区间,首先先形成如下表格
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
a b a b c b a c a d e f e g d e
8 5 8 5 7 5 8 7 8 14 15 11 15 13 14 15 最后出现位置
int hash[27]={0};
for(i=0;i<s.size();i++)//遍历形成最远位置数组
hash[s[i]-'a']=i;//s[i]-'a'=0,1,2 用于代表abcd,且i为最远出现位置,
//重复赋值即可得到字符的最远出现位置数组
vector result;
int left, right =0;
for(i=0;i<s.size();i++){
right=max(right,hash[s[i]-'a');//区间取到已包含字符的最远距离
//则其中出现的所有字符都被包含
if(i==right){
result.push_back(right-left+1);//返回区间长度
left=i+1;}}
return result;
贪心总结
思想很简单,局部到整体,但是有时候要借助创建的变量和方法确实难以想到,所以难点在于辅助的构造,而非算法本身。
动态规划
用于解决重叠子问题很多的问题,当前的每个状态都有上一个状态推导而来,可以说是大型的递归,我理解是在在运行中变化生成结果数组或者结果矩阵,故而称为动态规划。与贪心不同,贪心只是单纯地根据先有情况选出最优,而动态规划是需要推导得到最好结果。
一般流程
设置dp数组也就是结果集并搞懂dp[i]下标含义;
找到dp数组递推公式,即找到子问题的通解公式;
dp数组的初始化,具体问题具体分析;
确定遍历顺序;
输出打印dp数组,便于调试。
斐波那契数列
每个数为前两个数之和,求第n个数,以1,1开始。
直接递归或者单纯简单for循环
sum=dp[0]+dp[1];
dp[0]=dp[1];
dp[1]=sum;
就可以求,但是还是从简单问题理清思路,熟悉解决问题的一般流程。
dp[i]表示第i个数的值;
递推公式:dp[i]=dp[i-1]+dp[i-2]
数组初始化,dp[0]=1,dp[1]=1
遍历顺序从前至后,伪代码如下:
vector<int> dp(n+1);
dp[0]=1;dp[1]=1;
for(i=2;i<=n;i++)
dp[i]=dp[i-1]+dp[i-2];
return dp[n];
01背包
不同物品不同价值,背包最多能装的价值。
物品 0 1 2
重量 1 3 4
价值15 20 30 背包最大重量为4
首先可以使用暴力法,通过回溯列举所有可能性,每个物品取或者不取,复杂度为2的n次方。
dp数组含义: 使用动态规划是设置二维数组dp[i][j],代表[0,i]之间的物品,任意取放到容量为j的背包里的最大价值,不放物品i时的最大价值为dp[i-1][j],放了物品i的价值为dp[i-1][j-weight[i]]+value[i]。
递推公式: 解释一下就是根据物品,每次更新对比当前物品放进背包前后价值大小,取最大值,与贪心有点类似,但是贪心只会拿着大的就往包里塞,而动态规划则是边拿边算,如果当前价值更大就把前边放的乱七八糟东西拿出来,递推公式为
dp[i][j]=max(dp[i-1][j],dp[i-1][j-weight[i]]+value[i]
dp数组初始化: 二维表格可初始化如下:
ij 0 1 2 4 5
0 0 15 15 15 15
1 0
2 0
回顾对dp的定义:在i内任意取物品放到容量为j的价值,表格内现为已知元素,其余需要计算的元素如何定义呢?由递推式可知,每个元素都由上一层元素计算得来,故每次计算都会赋值且在计算之前与其他元素无关,初始化可任意。
遍历顺序:
for(物品){
for(背包容量)
递推公式}
即二维数组先填行数据,该遍历顺序由递推公式决定,因为当前元素要一来上一行元素。
滚动数组
用二维数组来解决01背包是一种比较基础的方法,但是该解空间有太大冗余,其实也可以压缩状态转而采用一维数组。
因为当前层是由上一层推导而来,如果我们将上一行拷贝到当前行,是不是就能将矩阵压缩成一行,而在过程中数组不断更新覆写,好像在向前滚动,故而称为滚动数组。
最长连续递增子序列
含义如题,例如1 3 5 4 7 序列输出3。
dp[i]表示以i为结尾的最长连续递增子序列长度。
因为只看连续,所以只需要比较dp[i]与dp[i-1]的大小即可,递推公式代码表示如下:
if(numb[i]>num[i-1]
dp[i]=dp[i-1]+1;
所有dp初始化为1;
遍历顺序从前向后
for(i=1;i<num,size();i++)
收集结果
if(dp[i]>result) result=dp[i]
动态规划总结
应该是这三个算法里最难的,到现在我也朦朦胧胧,感觉不做个十道八道题确实不能理解,时间所迫现在只能了解个大概,班门弄斧说说自己的想法:
动态规划就是更科学的贪心,通过对前人结果的计算来确定当下最正确的结果,在每个子问题中都得到正确的结果从而在整个问题正确,代码往往很简单,但是借助的dp数组及其含义和递推公式是难点。
简单算法总结
回溯是用递归代替for循环的更暴力的遍历,流程是先判断叶子节点,真则收回数据,否则一层for循环遍历节点引用递归函数实现深度优先遍历,结束后返回上一层。
核心就是深度优先加剪枝,其中剪枝是使回溯高效的关键环节,在for循环内部对节点进行判定后再递归,判断地越早越提前,减掉的枝越大,算法越高效。
贪心思路简单,局部最优推出整体最优,但是使用要注意两点:一是确认当前的局部最优能否推出整体最优;二是贪心的最优到底是谁与谁在何种情况下的最优。
该算法没有固定套路,只能具体问题具体分析,根据不同条件制定不同的贪心策略。
动态规划我也一知半解,斗胆胡言几句,见笑了。个人认为该算法是有根据的贪心,整体结果互相依赖时或者说所谓重叠子问题较多时使用,规模由小到大,层级由下到上,多个简单问题的最优解经过尝试比较出复杂问题的最优解。
实现上需要构造辅助数组来存储子问题的结果,建立辅助数组的递推公式,遍历问题输入集生成dp结果集合。