1循环神经网络
RNN通过将神经元串行起来处理序列化的数据。 由于每个神经元能用它的内部变量保存之前输入的序列信息,因此整个序列被浓缩成抽象的表示, 并可以据此进行分类或生成新的序列。
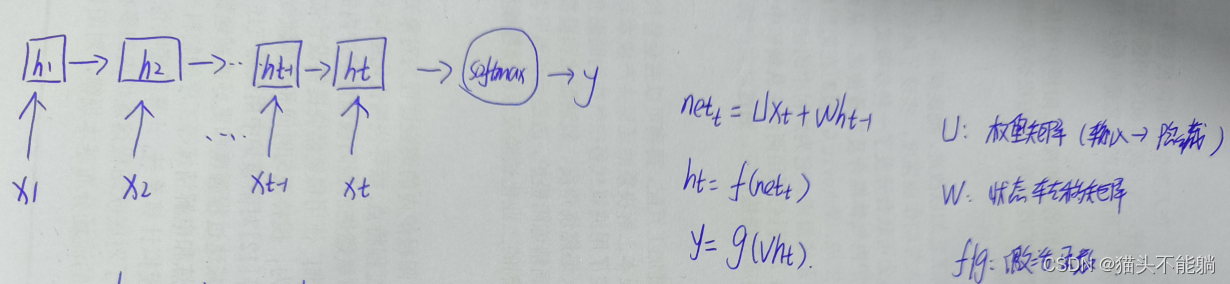
2 循环神经网络的梯度消失或梯度爆炸问题
传统的循环神经网络梯度可以表示成连乘的形式:

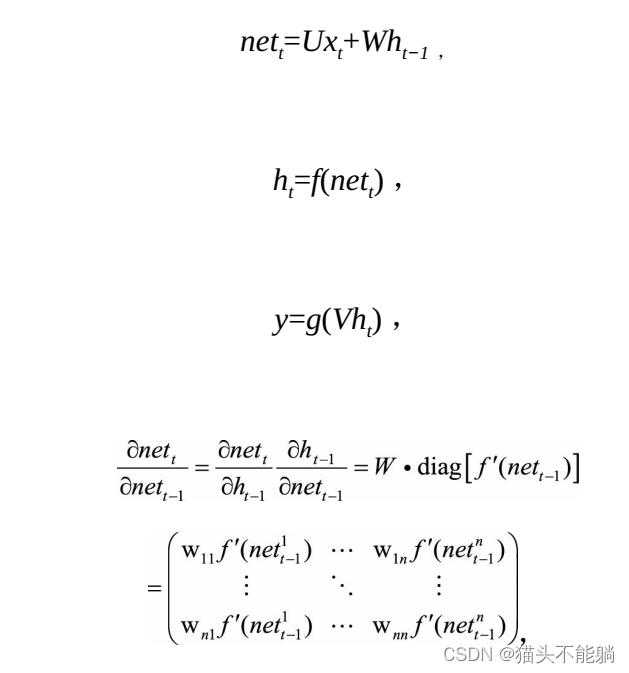
由于预测的误差是沿着神经网络的每一层反向传播的, 因此当雅克比矩阵的最大特征值大于1时, 随着离输出越来越远, 每层的梯度大小会呈指数增长, 导致梯度爆炸; 反之, 若雅克比矩阵的最大特征值小于1, 梯度的大小会呈指数缩小,产生梯度消失。
对于循环神经网络来说, 长短时记忆模型及其变种门控循环单元( Gated recurrent unit, GRU)等模型通过加入门控机制, 很大程度上弥补了梯度消失所带来的损失。
3循环神经网络的激活函数
根据前向传播公式向前传递一层, 可以得到
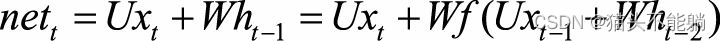
如果采用ReLU替代公式中的激活函数f, 并且假设ReLU函数一直处于激活区域(即输入大于0) , 则有f(x)=x,
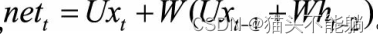
继续将其展开, 表达式中最终包含t个W连乘。 如果W不是单位矩阵,最终的结果将会趋于0或者无穷, 引发严重的数值问题。
当采用ReLU作为循环神经网络中隐含层的激活函数时, 只有当W的取值在单位矩阵附近时才能取得比较好的效果, 因此需要将W初始化为单位矩阵。 实验证明, 初始化W为单位矩阵并使用ReLU激活函数在一些应用中取得了与长短期记忆模型相似的结果, 并且学习速度比长短期记忆模型更快。
4 LSTM
4.1 LSTM结构图
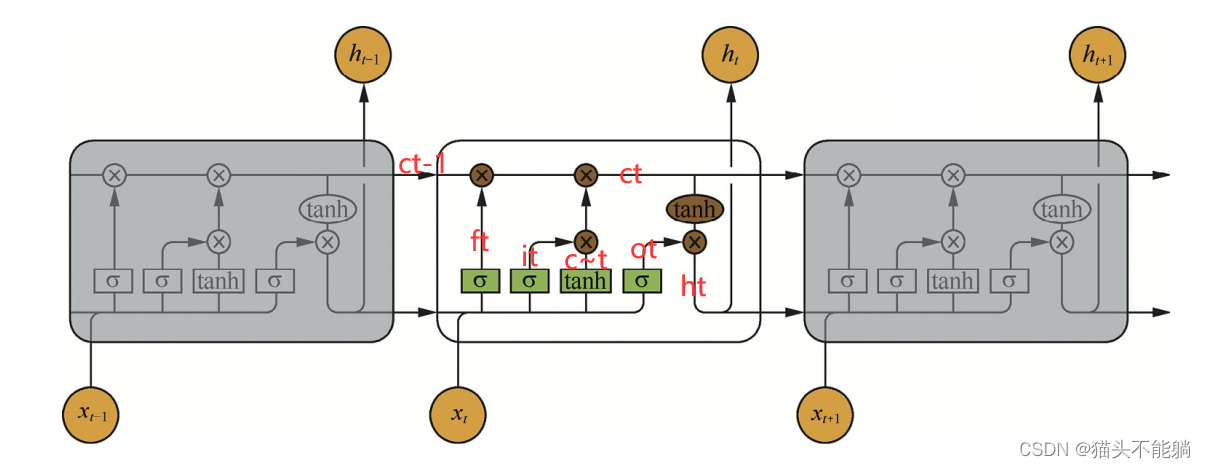 加入了输入门it、 遗忘门ft以及输出门ot三个门和一个内部记忆单元ct。 输入门控制当前计算的新状态以多大程度更新到记忆单元中; 遗忘门控制前一步记忆单元中的信息有多大程度被遗忘掉; 输出门控制当前的输出有多大程度上取决于当前的记忆单元。
加入了输入门it、 遗忘门ft以及输出门ot三个门和一个内部记忆单元ct。 输入门控制当前计算的新状态以多大程度更新到记忆单元中; 遗忘门控制前一步记忆单元中的信息有多大程度被遗忘掉; 输出门控制当前的输出有多大程度上取决于当前的记忆单元。
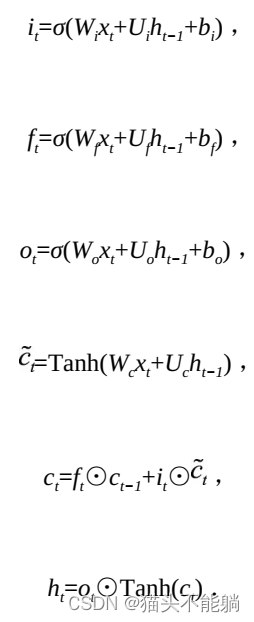
其中it是通过输入xt和上一步的隐含层输出ht−1进行线性变换, 再经过激活函数σ得到的。 输入门it的结果是向量, 其中每个元素是0到1之间的实数, 用于控制各维度流过阀门的信息量; Wi、 Ui两个矩阵和向量bi为输入门的参数, 是在训练过程中需要学习得到的。 遗忘门ft和输出门ot的计算方式与输入门类似, 它们有各自的参数W、 U和b。 与传统的循环神经网络不同的是, 从上一个记忆单元的状态ct−1到当前的状态ct的转移不一定完全取决于激活函数计算得到的状态, 还由输入门和遗忘门来共同控制。
4.2 LSTM激活函数
在LSTM中, 遗忘门、 输入门和输出门使用Sigmoid函数作为激活函数; 在生成候选记忆时, 使用双曲正切函数Tanh作为激活函数。 值得注意的是, 这两个激活函数都是饱和的, 也就是说在输入达到一定值的情况下, 输出就不会发生明显变化了。
5 Seq2Seq
5.1模型思想
Seq2Seq模型的核心思想是, 通过深度神经网络将一个作为输入的序列映射为一个作为输出的序列, 这一过程由编码输入与解码输出两个环节构成。 在经典的实现中, 编码器和解码器各由一个循环神经网络构成, 既可以选择传统循环神经网络结构, 也可以使用长短期记忆模型、 门控循环单元等。 在Seq2Seq模型中, 两个循环神经网络是共同训练的。
在文本摘要任务中, 输入的序列是长句子或段落, 输出的序列是摘要短句。在图像描述文本生成任务中, 输入是图像经过视觉网络的特征, 输出的序列是图像的描述短句。 进行语音识别时, 输入的序列是音频信号, 输出的序列是识别出的文本。
5.2 模型解码部分
Seq2Seq模型最核心的部分是其解码部分,最基础的解码方法是贪心法, 即选取一种度量标准后, 每次都在当前状态下选择最佳的一个结果, 直到结束。 贪心法获得的是一个局部最优解, 由于实际问题的复杂性, 该方法往往并不能取得最好的效果。
5.3模型解码改进
5.3.1 集束模型
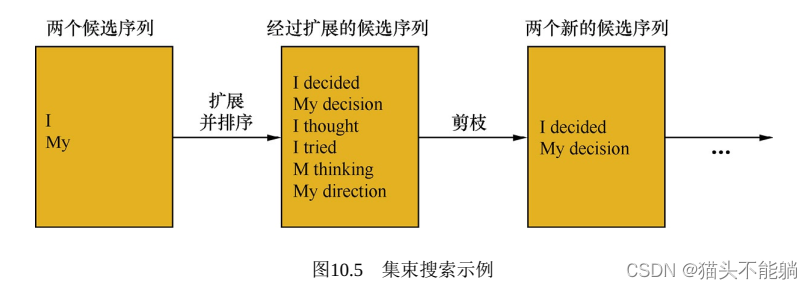
该方法会保存b当前的较佳选择, 然后解码时每一步根据保存的选择进行下一步扩展和排序, 接着选择前b个进行保存, 循环迭代, 直到结束时选择最佳的一个作为解码的结果。
堆叠的RNN、 增加Dropout机制、 与编码器之间建立残差连接等,均是常见的改进措施。
6 注意力机制
使用Seq2Seq模型, 通常会先使用一个循环神经网络作为编码器, 将输入序列(源语言句子的词向量序列) 编码成为一个向量表示; 然后再使用一个循环神经网络模型作为解码器, 从编码器得到的向量表示里解码得到输出序列(目标语言句子的词序列) 。随着序列增长,
句子越前面的词的信息丢失就越严重。

Seq2Seq模型中引入注意力机制就是为了解决上述的问题。 在注意力机制中,仍然可以用普通的循环神经网络对输入序列进行编码, 得到隐状态h1,h2…hT。 但是在解码时, 每一个输出词都依赖于前一个隐状态以及输入序列每一个对应的隐状态:

其中注意力权重参数αij并不是一个固定权重, 而是由另一个神经网络计算得到:
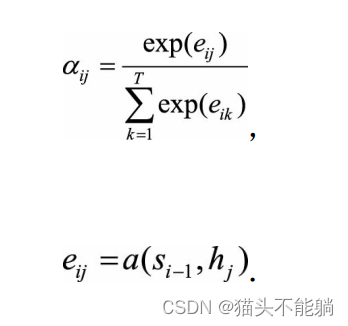
神经网络a将上一个输出序列隐状态si−1和输入序列隐状态hj作为输入, 计算出一个xj, yi对齐的值eij, 再归一化得到权重αij。
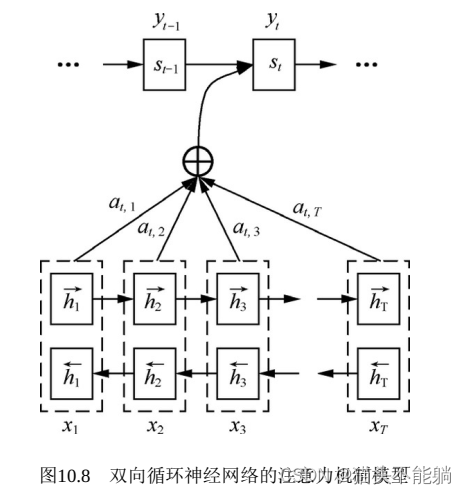
一个典型的Seq2Seq模型里, 生成一个输出词yj, 会用到第i个输入词对应的隐状态hi以及对应的注意力权重αij。 如果只使用一个方向的循环神经网络来计算隐状态, 那么hi只包含了x0到xi的信息, 相当于在αij这里丢失了xi后面的词的信息。
而使用双向循环神经网络进行建模, 第i个输入词对应的隐状态包含了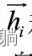
和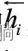 , 前者编码x0到xi的信息, 后者编码xi及之后所有词的信息, 防止了前后文信息的丢失。
, 前者编码x0到xi的信息, 后者编码xi及之后所有词的信息, 防止了前后文信息的丢失。