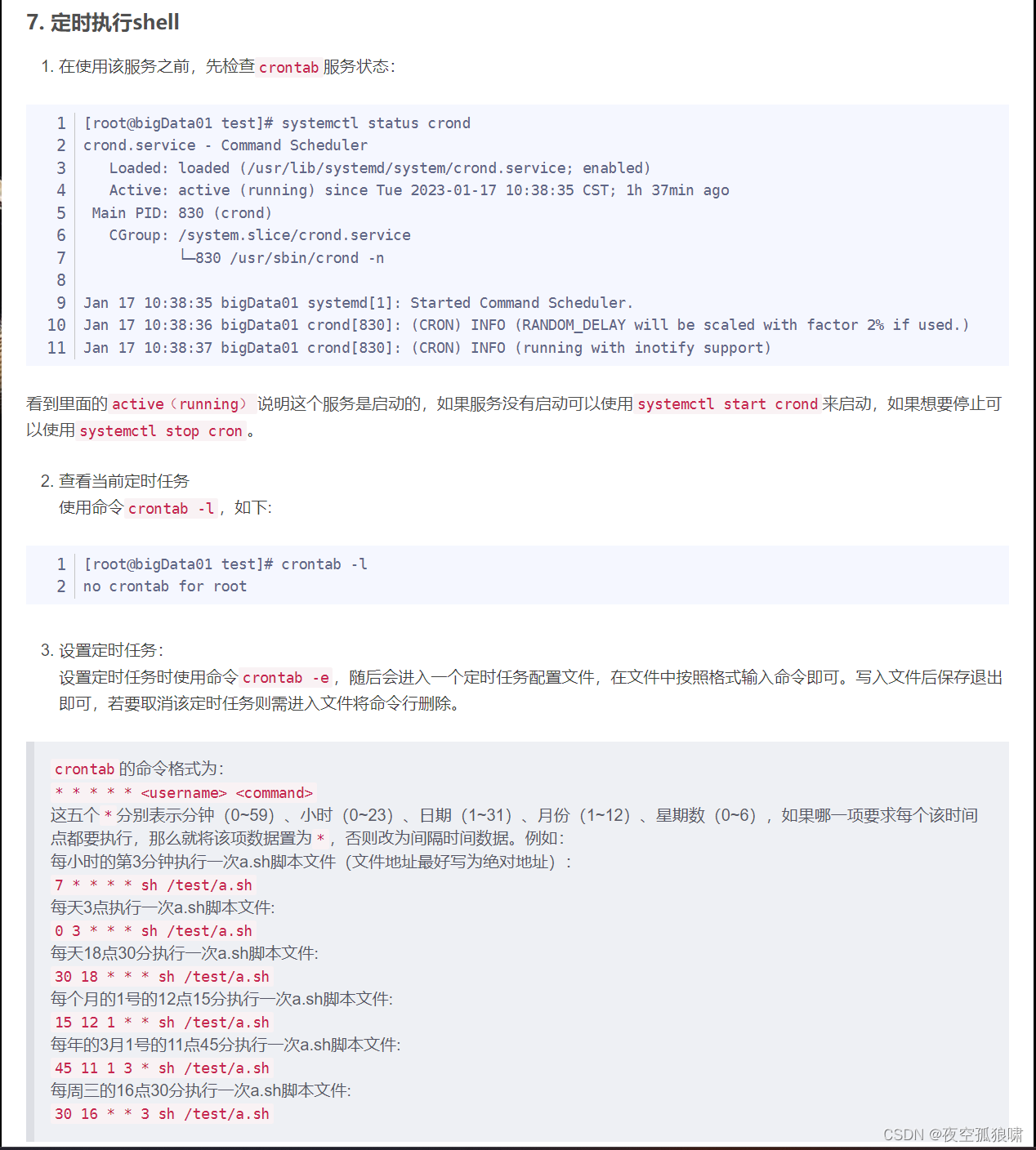
1. 决策树概念
通过不断的划分条件来进行分类,决策树最关键的是找出那些对结果影响最大的条件,放到前面。
我举个列子来帮助大家理解,我现在给我女儿介绍了一个相亲对象,她根据下面这张决策树图来进行选择。比如年龄是女儿择偶更看中的,那就该把年龄这个因素放在最前面,这样可以节省查找次数。收入高的话就去见,中等的话还要考虑工作怎么样。

决策树通过历史数据,找出数据集中对结果影响最大的特征,再找第二个影响最大的特征。若新来一个数,只要根据我们已经建立起的决策树进行归类即可。
2. 决策树的信息熵
用来表示随机数据不确定性的度量,信息熵越大,表示这组数据越不稳定,而信息熵越小,则数据越稳定、越接近、越类似。
信息熵公式: H(x)=−∑ni=1P(i)∗logP(i)2 代表某一个特征中每一个值出现的概率
上个例子中的年龄的基尼系数是:Gini(年龄) = 1 – (5/15)^2 - (5/15)^2 - (5/15)^2
在建立决策树时,基尼系数越小的,就把它放在最前面。
5. 预剪枝和后剪枝
树的层级和叶子节点不能过于复杂,如果过于复杂,会导致过拟合现象(过拟合:训练时得分很高,测试时得分很低)。预剪枝和后剪枝都是为了防止决策树太复杂的手段
5.1 预剪枝
在决策树的建立过程中不断调节来达到最优,可以调节的条件有:
(1)树的深度:在决策树建立过程中,发现深度超过指定的值,那么就不再分了。
(2)叶子节点个数:在决策树建立过程中,发现叶子节点个数超过指定的值,那么就不再分了。
(3)叶子节点样本数:如果某个叶子结点的个数已经低于指定的值,那么就不再分了。
(4)信息增益量或Gini系数:计算信息增益量或Gini系数,如果小于指定的值,那就不再分了。
优点:预剪枝可以有效降低过拟合现象,在决策树建立过程中进行调节,因此显著减少了训练时间和测试时间;预剪枝效率比后剪枝高。
缺点:预剪枝是通过限制一些建树的条件来实现的,这种方式容易导致欠拟合现象:模型训练的不够好。
5.2 后剪枝
在决策树建立完成之后再进行的,根据以下公式:
C = gini(或信息增益)*sample(样本数) + a*叶子节点个数
C表示损失,C越大,损失越多。通过剪枝前后的损失对比,选择损失小的值,考虑是否剪枝。
a是自己调节的,a越大,叶子节点个数越多,损失越大。因此a值越大,偏向于叶子节点少的,a越小,偏向于叶子节点多的。
优点:通常比预剪枝保留更多的分支,因此欠拟合风险比预剪枝要小。
缺点:但因为后剪枝是再数建立完成之后再自底向上对所有非叶子节点进行注意考察,因此训练时间开销比预剪枝要大。





![[Vue 代码模板] Vue3 中使用 Tailwind CSS + NutUI 实现侧边工具栏切换主题](https://img-blog.csdnimg.cn/img_convert/49ee8c9d2ce8de93dba9e046484addd4.png)