图像锐化1
获取源工程可访问huiningLi的gitee可在此工程的基础上进行学习。
实验要求
5.1实验目的、要求
实验目的:
(1)掌握图像增强的原理与相关方法。
(2)能使用VC++实现图像增强的一些相关功能。
实验要求:
A部分:
(1)对一幅256级灰度图像,使用VC++实现分段线性变换,直方图均衡化。
(2)对一幅256级灰度图像,使用VC++实现锐化处理(使用拉普拉斯算子)。
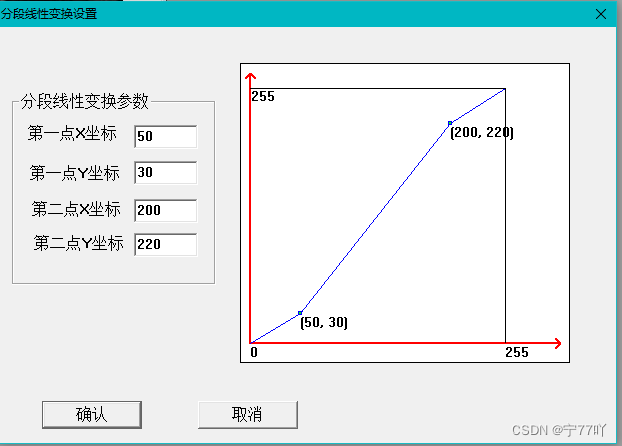
一、 分段线性变换
1. 分段线性变换的原理
灰度图像分段线性变换是一种调整图像灰度级别的方法,它通过将灰度范围划分为多个分段,然后对每个分段应用线性变换来调整图像的对比度和亮度。这种方法的主要目的是增强或减弱图像中特定灰度范围的细节,以改善图像的视觉效果。
下面是该方法的基本原理:
-
分段划分: 将整个灰度范围划分为多个不重叠的分段。每个分段代表图像中的一个灰度范围。这些分段由一个或多个分界点定义,这些分界点将整个灰度范围划分成不同的区域。
-
线性变换: 对每个分段应用线性变换。线性变换由斜率和截距两个参数定义。斜率决定了线的倾斜程度,而截距则控制了线的位置。通过调整这两个参数,可以实现对分段内灰度级别的调整。
-
像素更新: 对图像的每个像素应用上述的分段线性变换。首先,确定像素所属的分段,然后使用该分段对应的线性变换来更新像素的灰度值。这样,每个像素都会根据其原始灰度值和所属分段的线性变换进行调整。
通过灰度图像分段线性变换,可以实现对图像不同灰度范围的灰度级别进行差异化的调整。例如,可以增强图像中的低对比度区域或减弱过曝区域,从而更好地展现图像细节。这种方法在图像增强和调整方面具有一定的灵活性,但需要根据具体的应用场景和图像特性来选择适当的分段和线性变换参数。
2. 分段线性变换的实验代码
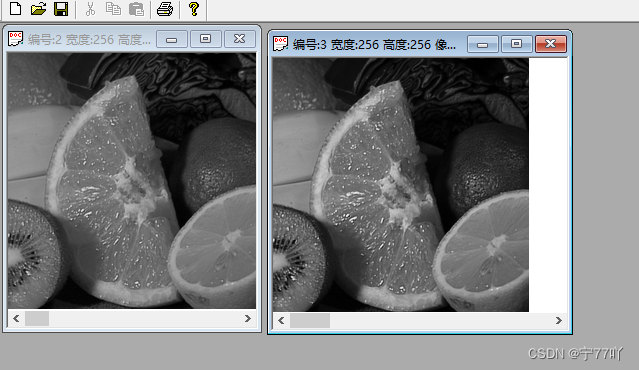
3. 分段线性变换的实验现象
左:原灰度图
右:灰度图像分段线性变换后
二、直方图均衡化
1. 直方图均衡化的原理
直方图均衡化是一种用于增强图像对比度的图像处理技术。其基本原理是将图像的灰度直方图变换成一个均匀分布的直方图,从而拉伸图像的灰度范围,使得亮度水平更加均匀,细节更为突出。
具体的步骤如下:
-
计算直方图: 统计图像中每个灰度级别的像素数量,形成直方图。
-
计算累积分布函数(CDF): 将直方图进行归一化,得到每个灰度级别对应的累积概率。
C D F ( i ) = ∑ j = 0 i P ( j ) CDF(i) = \sum_{j=0}^{i} P(j) CDF(i)=j=0∑iP(j)
其中, P ( j ) P(j) P(j) 是灰度级别 j j j 的概率。
-
直方图均衡化变换函数: 将CDF的值映射到新的灰度级别范围。
H ( i ) = round ( C D F ( i ) × ( L − 1 ) N ) H(i) = \text{round}\left(\frac{CDF(i) \times (L-1)}{N}\right) H(i)=round(NCDF(i)×(L−1))
其中, H ( i ) H(i) H(i) 是新的灰度级别, L L L 是灰度级别的最大值, N N N 是图像的总像素数量。 r o u n d ( ) round() round() 是一个数学函数,通常用于将一个浮点数四舍五入为最接近的整数
-
应用变换: 将变换函数应用于图像的每个像素,更新图像的灰度级别。
通过直方图均衡化,原始图像中灰度分布不均匀的区域会被映射到更广泛的灰度范围,从而提高了图像的对比度,使细节更加清晰。
2. 直方图均衡化的实验代码
BOOL HistogramEqualize(CDib* pDib){// 指向源图像的指针unsigned char* lpSrc;// 临时变量int nTemp;// 循环变量int i,j;// 累积直方图,即灰度映射表BYTE byMap[256];// 直方图int nCount[256];// 图象的高度和宽度CSize sizeImage;sizeImage = pDib->GetDimensions();// 获得图象数据存储的高度和宽度CSize SizeSaveImage;SizeSaveImage = pDib->GetDibSaveDim();// 重置计数为0for (i = 0; i < 256; i ++){// 清零nCount[i] = 0;}// 计算各个灰度值的计数,即得到直方图for (i = 0; i < sizeImage.cy; i ++){for (j = 0; j < sizeImage.cx; j ++){lpSrc = (unsigned char *)pDib->m_lpImage + SizeSaveImage.cx * i + j;//表示从图像数据的起始位置开始,跳过 i 行,再移动 j 列,最终指向了图像中第 i 行、第 j 列的像素的位置,获取图像中第 i 行、第 j 列的像素的灰度值// 计数加1nCount[*(lpSrc)]++;//以灰度值的大小为下坐标,进行计数}}// 计算累积直方图for (i = 0; i < 256; i++){// 初始为0nTemp = 0;for (j = 0; j <= i ; j++){nTemp += nCount[j];}// 计算对应的新灰度值---公式byMap[i] = (BYTE) (nTemp * 255 / sizeImage.cy / sizeImage.cx);}// 每行for(i = 0; i < sizeImage.cy; i++){// 每列for(j = 0; j < sizeImage.cx; j++){// 指向DIB第i行,第j个象素的指针lpSrc = (unsigned char*)pDib->m_lpImage + pDib->GetPixelOffset(i,j);// 计算新的灰度值x*lpSrc = byMap[*lpSrc];//找到当前像素的原始灰度值,并将其映射为新的灰度值。}}// 返回return TRUE;}
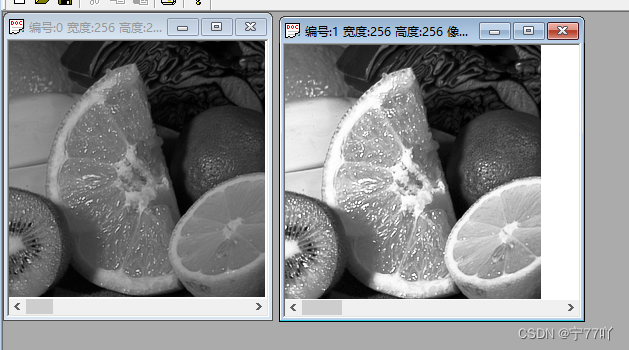
3. 直方图均衡化的实验现象
左:原图
右:直方图均衡化增强后
三、 拉普拉斯算子实现锐化
拉普拉斯算子的原理
拉普拉斯算子(Laplacian operator)是一种用于图像处理的滤波器,主要用于检测图像中的边缘和细节。它通过计算图像中每个像素点的二阶导数来实现。
拉普拉斯算子的一维形式为:
L ( x ) = d 2 d x 2 L(x) = \frac{d^2}{dx^2} L(x)=dx2d2
而在二维图像上的应用是通过以下离散形式的卷积核:
[ 0 1 0 1 − 4 1 0 1 0 ] \begin{bmatrix} 0 & 1 & 0 \\ 1 & -4 & 1 \\ 0 & 1 & 0 \\ \end{bmatrix} 0101−41010
应用拉普拉斯算子的过程是将这个卷积核与图像进行卷积运算。具体而言,对于图像中的每个像素,将其与卷积核中的对应元素相乘,然后将所有相乘的结果相加。这个过程可以用以下的数学表达式表示:
L ( x , y ) = ∑ i = − 1 1 ∑ j = − 1 1 kernel ( i , j ) × image ( x + i , y + j ) L(x, y) = \sum_{i=-1}^{1} \sum_{j=-1}^{1} \text{kernel}(i, j) \times \text{image}(x + i, y + j) L(x,y)=i=−1∑1j=−1∑1kernel(i,j)×image(x+i,y+j)
其中, kernel ( i , j ) \text{kernel}(i, j) kernel(i,j) 是卷积核中的元素, image ( x + i , y + j ) \text{image}(x + i, y + j) image(x+i,y+j) 是图像中对应位置的像素值。
拉普拉斯算子对图像进行了高通滤波,强调了图像中的高频细节和边缘。应用拉普拉斯算子后,边缘部分的像素值将发生变化,使得图像中的边缘更加明显。然而,拉普拉斯算子也会增加图像中的噪声。因此,在实际应用中,通常会结合其他技术,如平滑(低通滤波)来减少噪声的影响。
拉普拉斯算子的实验代码
/*************************************************************************** \函数名称:* LinearSharpen()** \输入参数:* LPBYTE lpImage - 指向图象数据得指针* int nWidth - 图象数据宽度* int nHeight - 图象数据高度** \返回值:* 无** \说明:* 线性锐化图象增强* 本函数采用拉普拉斯算子对图象进行线性锐化* 在原来图象上加上拉普拉斯算子锐化的信息***************************************************************************/
void LinearSharpen (LPBYTE lpImage, int nWidth, int nHeight)
{// 遍历图象的纵坐标int y;// 遍历图象的横坐标int x;double * pdGrad ;pdGrad = new double[nWidth*nHeight];//用于存储图像的梯度信息。// 初始化为0memset(pdGrad, 0, nWidth*nHeight*sizeof(double)) ;// 设置模板系数--设置拉普拉斯算子的卷积核,这是一个 3x3 的矩阵,用于计算图像中每个像素点的梯度。static int nWeight[3][3] ;nWeight[0][0] = -1 ; nWeight[0][1] = -1 ; nWeight[0][2] = -1 ; nWeight[1][0] = -1 ; nWeight[1][1] = 8 ; nWeight[1][2] = -1 ; nWeight[2][0] = -1 ; nWeight[2][1] = -1 ; nWeight[2][2] = -1 ; //这个变量用来表示Laplacian算子象素值int nTmp[3][3];// 临时变量double dGrad;// 模板循环控制变量int yy ;int xx ;for(y=1; y<nHeight-1 ; y++ )for(x=1 ; x<nWidth-1 ; x++ ){dGrad = 0 ; // Laplacian算子需要的各点象素值// 模板第一行nTmp[0][0] = lpImage[(y-1)*nWidth + x - 1 ] ; nTmp[0][1] = lpImage[(y-1)*nWidth + x ] ; nTmp[0][2] = lpImage[(y-1)*nWidth + x + 1 ] ; // 模板第二行nTmp[1][0] = lpImage[y*nWidth + x - 1 ] ; nTmp[1][1] = lpImage[y*nWidth + x ] ; nTmp[1][2] = lpImage[y*nWidth + x + 1 ] ; // 模板第三行nTmp[2][0] = lpImage[(y+1)*nWidth + x - 1 ] ; nTmp[2][1] = lpImage[(y+1)*nWidth + x ] ; nTmp[2][2] = lpImage[(y+1)*nWidth + x + 1 ] ; // 计算梯度for(yy=0; yy<3; yy++)for(xx=0; xx<3; xx++){dGrad += nTmp[yy][xx] * nWeight[yy][xx] ;}// 梯度值写入内存*(pdGrad+y*nWidth+x)=dGrad;}//将计算得到的梯度值加到原始图像上,实现锐化效果。for(y=0; y<nHeight ; y++ ){for(x=0 ; x<nWidth ; x++ ){lpImage[y*nWidth+x] = (unsigned char)max(0,min(255,(lpImage[y*nWidth+x] + (int)pdGrad[y*nWidth+x]) ));}}//释放申请的内存delete []pdGrad ;pdGrad = NULL ;
}
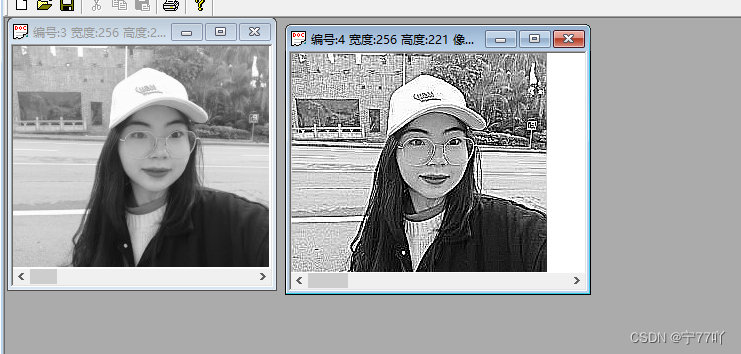
拉普拉斯算子的实验现象
左:原图
右:经过拉普拉斯锐化