书接上文漫谈广告机制设计 | 万剑归宗:聊聊广告机制设计与收入提升的秘密(2),我们聊到囚徒困境是完全信息静态博弈,参与人存在占优策略,最终达到占优均衡,并且是对称占优均衡。接下来我们继续举例子说明一些博弈论的概念,并向读者们灌输一个思想:做机制设计要分析各方利益得失,要指哪打哪,而不是毫无目的地探索尝试。
(一)
下面这个例子叫智猪博弈。
假设猪圈里有一头大猪、一头小猪,都是聪明的猪。猪圈的一头有猪食槽,另一头安装着控制猪食供应的按钮,按一下按钮会有10个单位的猪食进槽,但是谁按按钮就会首先付出2个单位的成本。按钮和猪食槽在相反位置,按按钮的猪要付出2个单位的成本,并且丧失了先到槽边进食的机会。若小猪先到槽边进食,因为缺乏竞争,进食的速度一般,最终大小猪吃到食物的比率是6∶4;若大猪先到槽边进食,大猪会霸占剩余所有猪食,最终大小猪收益比9∶1;若同时到槽边进食,大猪进食速度加快,最终大小猪收益比是7∶3。
用博弈论中的报酬矩阵可以更清晰地刻画出大猪和小猪的选择情况。如当大猪和小猪都选择行动时,各自都会付出2个单位的成本,获得的收益是7:3,最终的效用是5:1。下面我们分析一下大猪和小猪是否有最优的策略。

对于大猪而言,如果小猪行动,那么大猪行动的效用是5,等待的效用是9,那么大猪的最优策略是等待;如果小猪等待,那么大猪行动的效用是4,等待的效用是0,那么大猪的最优策略是行动。也就是说大猪的最优策略依赖小猪的策略。
对于小猪而言,如果大猪行动,那么小猪行动的效用是1,等待的效用是4,那么小猪的最优策略是等待;如果大猪等待,那么小猪行动的效用是-1,等待的效用是0,那么小猪的最优策略还是等待。也就是说无论大猪做什么策略,小猪的最优策略都是等待,在这种情况下,大猪不得不选择行动,最后大猪的效用是4,小猪的效用也是4,小猪"搭了便车"。
这样的例子可以用来解释现实生活中为什么能者必须多劳的问题,比如为什么市场的先行者获得效用可能还不如后来者,职场中有能力的人不一定获得比平庸者更高的效用,花钱投放广告的人最终可能是替竞对做了宣传。
这个博弈最终也会达到均衡状态,即大猪行动,小猪等待,这个均衡称之为重复剔除的占优策略均衡。这个均衡相比占优均衡变弱了一些。
(二)
接下来说明一下纳什均衡(约翰·纳什于获得1994年诺贝尔经济学奖)。

一个博弈有两个参与人,他们的策略和收益情况用以下收益矩阵表示。
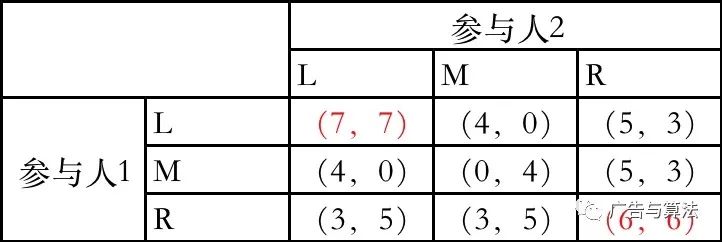
图中参与人1执行L策略,参与人2执行L策略,或者参与人1执行R策略,参与人2执行R策略均称之为纳什均衡,即当所有参与人持对应策略后,任一参与人均无诱因偏离这一均衡。可以看出纳什均衡不唯一。可见纳什均衡相比占优均衡要更弱一些。
然后我们举个猜拳的例子,石头剪刀布,其收益矩阵如下:
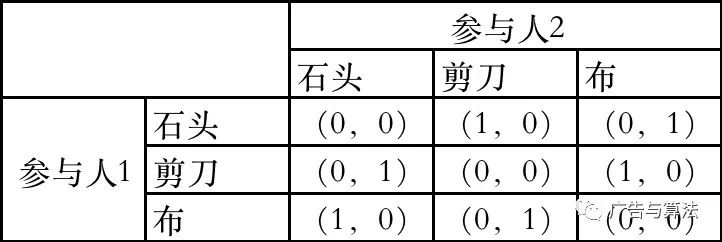
分析收益矩阵会发现,这个博弈连上面说的纳什均衡都没有。我们把策略从纯策略扩展到混合策略,纯策略是指以100%的概率执行某个策略,混合策略是以不同的概率执行不同的策略,整体概率为100%。那在猜拳游戏中,参与人的最优混合策略可以计算出来,就是随机出石头、剪刀、布,三个策略的概率分别是1/3,1/3,1/3,这也是符合基础认知的。这个平衡状态称之为混合策略纳什均衡。

好了,关于博弈论的例子我们就举到这里。读者们需要理解几个概念:不完全信息静态博弈、占优均衡<重复剔除占优均衡<纯策略纳什均衡<混合策略纳什均衡(<的含义是包含于的意思)。在每个有限策略式博弈(参与人和战略数据均有限)都存在纳什均衡,但有可能是混合战略纳什均衡。
拍卖属于博弈论的范畴,因此分析拍卖者在这场博弈中的利益情况,并基于利益情况设置想要的机制是十分重要的。特别地,当机制的参数或者机制本身变动时,或者广告模型或者排序策略更新都需要考虑一下广告主的反应的,而这种反应可能是长期的,AB试验看不出来的,甚至无法自证的,这也造成了目前的广告机制设计要么返祖到运筹优化,要么进化到深度学习模型,前几年微软亚研院的刘铁岩老师提出的算法博弈论的概念也逐渐势微,各种模型引入历史出价和分配结果的情况大行其道。
机制设计者追求的机制是参与各方能够真实报出内心的价值,这样机制设计者才能把有限的资源分配给最能创造价值的人手里,达到社会效率最大化。当然,这个理想十分美好。
(三)
言归正传,我们介绍拍卖的知识。
印象中的拍卖是一个拍卖师,对台下的买主喊着『十万一次,十万两次,十万三次』,然后以『成交』作为拍卖的结束,商品以十万卖出,可以发现拍卖是一种价格发现机制,这种机制在一系列明确的规则下,由投标人的报价确定某种资源的配置并形成最终的交易价格。也就是说通过竞价,将潜在的买主意愿支付的信息引导出来,拍卖品的分配和需要支付的价格均基于买主的报价。拍卖包含两个必要的要素:确定配置资源与支付价格的规则和买者的报价。拍卖应该与人们的商品交易活动同时出现,是一种十分古老的交易形式,那时候可能也有叫价举牌。拍卖也有着不光彩的历史,有文字记载的拍卖是古巴比伦时期的拍卖『新娘』,但就拍卖本身与而言,与现在的拍卖没有多大区别。中国最早有文字记载的拍卖活动在唐朝。后来拍卖不断延伸到商品交易的各个领域,拍卖和固定价格(非买主报价)相结合构成了经济生活的方方面面。
从不完全信息博弈的角度看拍卖,拍卖是出售者与竞买者的博弈,这种博弈的形式是丰富多彩的,可以从下图看出各式各样的拍卖。引用戎文晋 老师的《关键词拍卖与理论实践》。

从前面的图中看出,拍卖的应用形式是千变万化,丰富多彩的,但是人们总想从复杂的形式中抽象出基本形式,万变不离其宗,抓住本质就好分析问题了。不同拍卖形式之间的本质差别是在于资源的分配规则、支付规则和报价方式。1980年Engelbrecht-Wiggans 提出了这样分类方法,将拍卖分为以下四种:
1)公开增价拍卖(英式拍卖):这就是最常见的拍卖了,竞买者公开报价加价,直到没有人加价为止,最后一个加价的人获得拍卖品,并支付其报价。分配原则:价高者得,支付规则:自己的报价,报价方式:公开报价加价。注意:在这个过程中竞买人知道了其他竞买人的价格。古董和艺术品拍卖常用这种形式。
2)公开减价拍卖(荷兰式拍卖):出售者从一个很高的价格不断减价,直到有竞买者购买,并支付当前价格。因荷兰的郁金香拍卖得名,许多农产品常采用这种形式,拍卖速度比较快。注意虽然公开拍卖,但在这个过程中竞买人仅知道最终的成交价格,并不知道其他竞买人的心理价格。
3)第一价格密封拍卖(FP):竞买者秘密地向出售者提供一个报价,不让其他竞买者知道,价高者得,支付其报价。
4)第二价格密封拍卖(SP):竞买者秘密地向出售者提供一个报价,不让其他竞买者知道,价高者得,支付不是价高者的报价,而是第二高的报价。
这四种形式并非涵盖所有的拍卖形式,但是大部分拍卖是其延伸或者扩展。拍卖的形式有很多种,对于买卖双方来说,都想需求一个最好的形式。这就需要有指标来衡量不同拍卖形式的好坏,指标主要有两个:一个是拍卖效率(也有叫社会效率,社会福利等),这里是指拍卖品被愿意出最高价的竞买者拍到,另一个是卖者的收益,卖者期望的是拍卖收益最大。需要特别指出的,拍卖效率和平台收益有时候不可兼得。
(四)
虽然说拍卖的历史非常悠久,但选择哪种拍卖形式,拍卖效率最大,卖者收益最大呢?直到1961年,威廉·维克里(William Vickrey)针对这几种拍卖形式进行了数学建模,提出了一个独立私人价值模型(IIPV),才得到了一些很重要的结论,也因此获得1996年的诺贝尔经济学奖。

既然是数学建模,那么必定有前提假设条件了。
首先是单物品建模:这个物品不可分割售卖,这是最简单的拍卖形式。(这里特别说明一下:在真实的广告位或者关键词拍卖中,有时候是以多物品拍卖的形式进行的,单物品拍卖下得到的结论不一定适用于多物品拍卖)。
其次是私有估值,并且是独立、对称估值:在这个单物品拍卖中,存在多个竞买者,他们对拍卖物品的估值仅仅依赖于自身的私人信息,不受他人信息影响。(如果受到他人影响,这个估值不再是私人估值,而是关联估值)。独立对称估值是指竞价者估值是相互独立的随机变量,并遵循同一个连续随机变量的概率分布。竞买人除了知道自己的估价外,对于价值分布也完全清楚,只是不知道其他人具体的值。另外竞拍的人数也是共同的知识。
然后是个体理性:估值为0的竞买人其预期支付也为0(拍卖胜出的支付不会超过其出价)
最后是风险中性:竞买人在拍卖中的目标是最大化自己的预期收益,即:预期收益 = 胜出的概率 * (估值 - 胜出计费)- (1- 胜出的概率) * 失败的付费。注意该预期收益是加性可分离的,也就是说不受预算限制、ROI限制等等影响。
(五)
基于IIPV模型,我们来分析一下四种基础拍卖形式下竞买人的竞价策略,均衡状态及其在均衡时的社会效率和卖者收益的情况。因为从竞价策略上分析,荷兰式拍卖与第一价格密封拍卖存在等价策略。在私人价值假设(仅需这一个假设)上,英式拍卖与第二价格密封拍卖存在等价策略。因此来说仅仅分析第一价格密封拍卖和第二价格密封拍卖即可。
这里的策略就是报价。因为竞买人是对称的,所以只用考虑一个典型的竞买人策略,即对于每一个估价v_i选择一个报价b_i,报价策略函数为b_i= B(v_i)。对于一个竞买人来说,他的目的是寻找一个最优报价策略函数B,使得自己的收益最大化。
如果采用第二价格密封拍卖(SP),那么竞买人的最优报价策略函数是什么呢?这里直接给出结论了,竞买人的占优策略就是说出真实报出内心的估价,即b_i = v_i(感兴趣的话可以去看克里斯纳写的《拍卖理论》书中的证明)。最终SP下的均衡是对称占优均衡,社会效率是最大的,因为竞买人真实报出了内心估价,物品又是分配给报价最高的人,对应卖者的收益是次高位的报价。SP的伟大之处在于每个人都在追求私人价值最大化的同时,整体的效率最大化。
如果采用第一价格密封拍卖(FP), FP的报价策略和均衡分析要比SP复杂得多。具体推导过程不再描述(感兴趣可以看《拍卖理论》),这里直接给结果。在FP中,竞买人没有纯占优策略,存在混合策略,即竞买人的均衡报价策略是在假定自己获胜的情况下,对第二高估值的期望值。因此,在均衡的时候,每一个竞买人都会隐藏一部分自己的私人信息,随着参与竞拍人数增加,竞买人的均衡报价将越来越接近其真实估价。所以在FP下的均衡是对称混合纳什均衡,存在社会效率损失的可能。
那么对于售卖者来说,十分迫切地想知道选择哪种拍卖形式可以收益最大化呢?很不幸,Vickrey给出了令人吃惊的答案,这四种拍卖形式对售卖者来说收益是相同的,这就是收益等价原理。
乍一看,第一价格密封拍卖与第二价格密封拍卖的收益应该不一样呀,两者的分配规则是一致的,区别仅在于支付规则,因此采用二价机制很容易遭受损失,但是忘了一个基本问题,因为支付规则不同,两者的分报价策略也是不一样的。前者,竞买者的预期支付依赖于自己的报价,自然会对自己的估价有所隐藏;后者的预期支付与自己的报价无关,会更加积极的报价。
不过,需要注意,虽然存在等价原理,但是并不代表售卖者不需要做决策了。首先,收益等价原理是有前提假设的,即私人价值模型;其次,即使在私人价值模型的前提下,售卖者还有其他的拍卖形式(如全支付拍卖,两阶段拍卖,带有入场费和保留价的拍卖)等可供选择和参数设置,而这部分工作其实也是机制工作的重要部分。
比如,第二价格拍卖下的收益,要比第一价格拍卖下的更加多变,前者的价格区间为整个策略集合,也就是说前者的拍卖风险更大,对于风险厌恶的售卖者来说都会相对偏爱后者,这也就解释了现实生活着的艺术品等大部分采用了第一价格拍卖。
(六)
对于研究者,最重要的能力是建模的能力,就是思考怎么用数学语言,计算机语言描述世界的能力,这也正是学习和教育真正需要培养的能力,而很多情况下,我们已经以考试为导向的教育毁得体无完肤,学习的目的不是认知这个世界,而是变成了考试的分数,找到一份体面的工作,这是一件多么悲哀的事情啊!如今已经毕业多年,在工作中,良师益友难寻,也最需要这样一份能力,还需要一遍遍看书去领悟。我们下篇文章继续介绍,GFP, GSP,以及万剑归宗的第一层口诀心法:排序变换与收益最大化。敬请关注。
参考资料:
[1] 戎文晋 【关键词拍卖与理论实践】
[2] 克里斯纳,罗德明翻译【拍卖理论】