掀开一幕幕精彩剧情,手机已经成为了我们身边必不可少的追剧神器。在这个信息爆炸的时代,我们渴望能够随时随地享受到精彩的影视作品,尤其是在家的休息的时候,希望电视也能同手机一样,想看啥就搜啥。酷开科技大内容战略,让你在家也能轻松打破时间和空间的限制,畅快追剧!不仅提供了丰富多样的内容,还拥有出色的消费者体验和强大的功能,让你完全沉浸在大屏之中!
酷开科技联手腾讯、爱奇艺两大视频巨头,打造5大片库,12个频道,内含万余部电影,上万部电视剧和综艺节目,各种内容应有尽有。依托酷开系统,将海量影视资源全部展现出来,更有酷开科技影视VIP特权,新片速递尝鲜,高速通道观影,尽享不一样的大屏VIP体验。
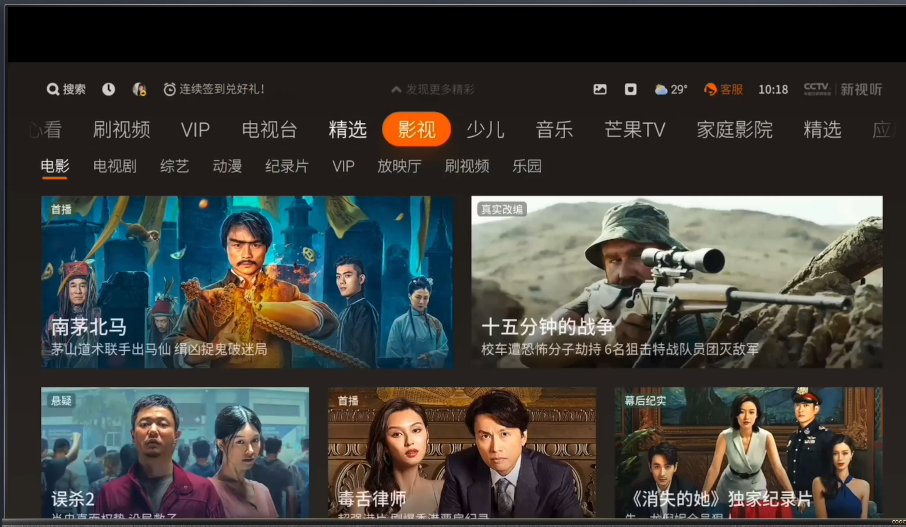
无论你是追求国内热播剧,还是钟情于海外大片,酷开系统都能满足你的口味!在酷开系统中,汇总了当下的热播作品,看热剧不迷路;另外还有更细致的分类,包括电影、综艺、连续剧、动漫……各类型都做了好剧推荐,满足各大粉丝的不同看剧需求,想看什么类型的,划动手指轻松就能找到,看剧从来没有这么轻松过!
除了资源足够多,在酷开系统中的智慧AI还能根据消费者的观看行为数据,通过分析消费者的观看喜好,智能推荐给消费者高匹配度的内容,实现千人千面的精准推荐。这样贴心的技术,能够为每个人提供专属的内容推荐,让你每次使用酷开系统,都能透过推荐内容找到自己喜欢的节目。如此贴心的酷开系统难道还不能赢得你的青睐嘛~


![[计算机网络]网络层概述](https://img-blog.csdnimg.cn/132d2527fc6b49d6b3319146de3b16ee.png)