一、介绍
您知道第一个神经网络是在 20 世纪 50 年代初发现的吗?
深度学习 (DL) 和神经网络 (NN) 目前正在推动本世纪一些最巧妙的发明。他们从数据和环境中学习的令人难以置信的能力使他们成为机器学习科学家的首选。
深度学习和神经网络是自动驾驶汽车、图像识别软件、推荐系统等产品的核心。显然,它是一种强大的算法,对各种数据类型也具有高度适应性。
人们认为神经网络是一个极其难学的课题。因此,要么他们中的一些人不使用它,要么使用它的人将其用作黑匣子。在不知道如何完成某件事的情况下做这件事还有意义吗?不!
在本文中,我试图用简单的语言解释神经网络的概念。理解这篇文章需要一点生物学知识和很大的耐心。读完本文后,您将成为一名自信的分析师,准备开始使用神经网络。如果有什么不明白的地方,可以在评论区留言。
注意:本文最适合数据科学和机器学习领域的中级用户。初学者可能会发现它具有挑战性。

二、目录
- 介绍
- 什么是神经网络?
- 单个神经元如何工作?
- 示例 1:与
- 示例 2:或
- 示例 3:NOT
- 为什么多层网络有用?
- 情况1:X1 XNOR X2 = (A'.B') + (AB)
- 情况 2: X1 XNOR X2 = NOT [ (A+B).(A'+B') ]
- 神经网络的一般结构
- 反向传播
- 经常问的问题
- 尾注
三、什么是神经网络?
神经网络(NN),也称为人工神经网络,因其对人类神经系统工作的人工表示而得名。还记得这张图吗?我们大多数人都在高中接受过教育!
闪回回顾:让我们首先了解我们的神经系统是如何工作的。 神经系统 由数百万个神经细胞或神经元组成。神经元具有以下结构:

主要组成部分是:
- 树突 - 它以电脉冲的形式从其他神经元获取输入
- Cell Body – 它根据这些输入产生推论并决定采取什么行动
- 轴突终端– 以电脉冲形式传输输出
简单来说,每个神经元通过树突从许多其他神经元获取输入。然后,它对输入执行所需的处理,并通过公理将另一个电脉冲发送到终端节点,从那里传输到许多其他神经元。

ANN 的工作方式非常相似。神经网络的一般结构如下所示:来源
该图描绘了一个典型的神经网络,其中单独解释了单个神经元的工作。让我们来理解这一点。
每个神经元的输入就像树突。就像人类神经系统一样,神经元(尽管是人工的!)整理所有输入并对它们执行操作。最后,它将输出传输到与其连接的所有其他神经元(下一层)。神经网络分为 3 种类型的层:
- 输入层: 训练观察结果通过这些神经元馈送
- 隐藏层: 这些是输入和输出之间的中间层,帮助神经网络学习数据中涉及的复杂关系。
- 输出层: 最终输出是从前两层中提取的。例如:如果分类问题有 5 个类别,则稍后的输出将有 5 个神经元。
让我们首先通过示例研究每个神经元的功能。
四、单个神经元如何工作?
在本节中,我们将通过简单的示例探讨单个神经元的工作原理。这个想法是让您直观地了解神经元如何使用输入计算输出。典型的神经元如下所示:

不同的组件是:
- x 1 , x 2 ,…, x N: 神经元的输入。这些可以是来自输入层的实际观察值,也可以是来自隐藏层之一的中间值。
- x 0: 偏置单位。这是添加到激活函数输入的常数值。它的工作原理与截距项类似,通常具有 +1 值。
- w 0 ,w 1 , w 2 ,…,w N: 每个输入的权重。请注意,即使是偏差单位也有权重。
- a: 神经元的输出,计算公式为:

这里f是已知的激活函数。这使得神经网络极其灵活,并具有估计数据中复杂非线性关系的能力。它可以是高斯函数、逻辑函数、双曲函数,甚至在简单情况下可以是线性函数。
让我们使用神经网络实现 3 个基本功能 – OR、AND、NOT。这将帮助我们了解它们是如何工作的。您可以假设这些就像一个分类问题,我们将预测不同输入组合的输出(0 或 1)。
我们将使用以下激活函数对它们进行建模,就像线性分类器一样:

示例 1:与
AND 函数可以实现为:

该神经元的输出为:
a = f(-1.5 + x1 + x2 )
此实现的真值表是:

到这里我们可以看到AND函数已经成功实现了。列“a”符合“X1 AND X2”。请注意,此处偏差单位权重为-1.5。但这不是一个固定值。直观上,我们可以将其理解为只有当x 1和x 2都为正时,使得总值为正的任何东西。所以 (-1,-2) 之间的任何值都可以。
示例 2:或
OR 函数可以实现为:

该神经元的输出为:
a = f(-0.5 + x1 + x2 )
此实现的真值表是:

列“a”符合“X1 OR X2”。我们可以看到,仅仅通过改变偏置单元权重,我们就可以实现一个OR函数。这与上面的非常相似。直观上你可以理解,这里的偏置单位是这样的:如果x1或x2中的任何一个变为正值,则加权和将为正值。
示例 3:NOT
就像前面的情况一样,NOT 函数可以实现为:

该神经元的输出为:
a = f( 1 – 2*x1 )
此实现的真值表是:

再次,符合期望值证明了功能。我希望通过这些示例,您能够对神经网络内的神经元如何工作有一些直观的了解。这里我使用了一个非常简单的激活函数。
注意:通常 会使用逻辑函数来代替我在这里使用的函数,因为它是可微的并且可以确定梯度。只有 1 个捕获点。也就是说,它输出的是浮点值,而不是精确的 0 或 1。
五、为什么多层网络有用?
在了解单个神经元的工作原理之后,让我们尝试了解神经网络如何使用多层来建模复杂的关系。为了进一步理解这一点,我们将以XNOR 函数为例。回顾一下,XNOR 函数的真值表如下所示:

在这里我们可以看到,当两个输入相同时,输出为 1,否则为 0。这种关系无法使用单个神经元进行建模。(不相信我?尝试一下!)因此我们将使用多层网络。使用多层背后的想法是可以将复杂的关系分解为更简单的函数并进行组合。
让我们分解一下 XNOR 函数。
X1 XNOR X2 = NOT ( X1 XOR X2 )= NOT [ (A+B).(A'+B') ] (注意:这里 '+' 表示 OR,'.' 表示 AND)= (A+B)' + (A'+B')'= (A'.B') + (AB)现在我们可以使用任何简化的情况来实现它。我将通过两个案例向您展示如何实现这一点。
情况1:X1 XNOR X2 = (A'.B') + (AB)
这里的挑战是设计一个神经元来建模 A'.B' 。这可以使用以下内容轻松建模:

该神经元的输出为:
a = f( 0.5 – x1 – x2 )
该函数的真值表为:
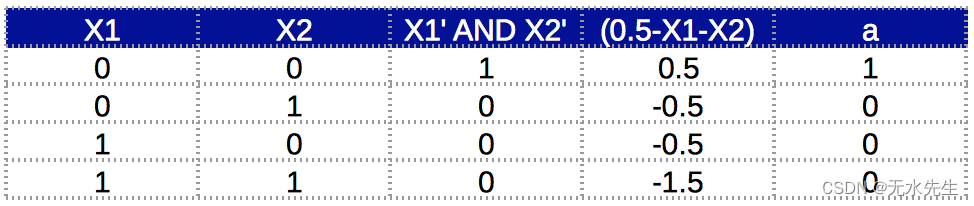
现在我们已经对各个组件进行了建模,我们可以使用多层网络将它们组合起来。首先,让我们看一下该网络的语义图:

这里我们可以看到,在第 1 层,我们将分别确定 A'.B' 和 AB。在第 2 层中,我们将获取它们的输出并在顶部实现 OR 函数。这将完成整个神经网络。最终的网络如下所示:

如果你仔细观察,这只不过是我们已经绘制的不同神经元的组合。不同的输出代表不同的单位:
- a 1 :实现 A'.B'
- a 2 :实现AB
- a 3:实现适用于 a1 和 a2 的 OR,因此有效 (A'.B' + AB)
可以使用真值表验证功能:

我想现在您可以对多层的工作原理有一些直观的了解。让我们对同一案例进行另一个实现。
情况 2: X1 XNOR X2 = NOT [ (A+B).(A'+B') ]
在上面的例子中,我们必须分别计算A'.B'。如果我们只想使用基本的 AND、OR、NOT 函数来实现该函数该怎么办?考虑以下语义:

在这里您可以看到我们必须使用 3 个隐藏层。工作将与我们之前所做的类似。网络看起来像:

这里神经元执行以下操作:
- a 1 :与A相同
- a 2 :实现 A'
- a 3 :与B相同
- a 4 :实现 B'
- a 5:实现 OR,实际上是 A+B
- a 6:实现 OR,实际上是 A'+B'
- a 7 :有效地实现 AND (A+B).(A'+B')
- a 8:实现 NOT,实际上 NOT [ (A+B).(A'+B') ],这是最终的 XNOR
请注意,通常一个神经元会馈送到下一层的除偏置单元之外的所有其他神经元。在本例中,我消除了从第 1 层到第 2 层的一些连接。这是因为它们的权重为 0,添加它们会使视觉上难以掌握。
真值表为:

最后,我们成功实现了XNOR功能。此方法比情况 1 更复杂。因此,您应该始终首选情况 1。但这里的想法是展示如何将复杂的功能分解为多个层。我希望现在多层的优势更加明显。
六、神经网络的一般结构
现在我们已经了解了一些基本示例,让我们定义每个神经网络所属的通用结构。我们还将看到在给定输入的情况下确定输出所遵循的方程。这称为 前向传播。
通用神经网络可以定义为:

它有 L 层,其中 1 个输入层、1 个输出层和 L-2 个隐藏层。术语:
- L:层数
- N i:第i层神经元数量(不包括偏置单元),其中i=1,2,…,L
- a i (j):第 i 层第 j 个神经元的输出,其中 i=1,2…L | j=0,1,2….N i
由于每层的输出形成下一层的输入,因此我们定义方程,以使用第 i 层的输出作为输入来确定第 i+1 层的输出。
第i+1层的输入为:
A i = [ a i (0) , a i (1) , ......, a i (N i ) ]
suze:1×N i +1第i层到第i+1层的权重矩阵为:
W (i) = [ [ W 01 (i) W 11 (i) ....... W N i 1 (i) ][ W 02 (i) W 12 (i) ....... W N i 2 (i) ]……………………[ W 0N i+1 (i) W 1N i+1 (i) ....... W N i N i+1 (i) ] ]尺寸:N i+1 x N i +1第i+ 1层的输出可以计算为:
A i+1 = f( A i .W (i) )
尺寸:1×N i+1对每个后续层使用这些方程,我们可以确定最终输出。输出层中神经元的数量取决于问题的类型。对于回归或二元分类问题,它可以是 1;对于多类分类问题,它可以是多个。
但这只是确定 1 次运行的输出。最终目标是更新模型的权重以最小化损失函数。权重使用反向传播算法进行更新,我们接下来将研究该算法。
七、反向传播
反向传播 (BP) 算法的工作原理是确定输出的损失(或误差),然后将其传播回网络。更新权重以最小化每个神经元产生的误差。我不会详细介绍该算法,但我会尝试让您直观地了解它的工作原理。
最小化误差的第一步是确定每个节点的梯度。最终输出。由于它是一个多层网络,确定梯度并不是很简单。
让我们了解多层网络的梯度。让我们从神经网络退后一步,考虑一个非常简单的系统,如下所示:

这里有3个输入,简单处理为:
d = a – b
e = d * c = (ab)*c
现在我们需要确定 a、b、c、d 对于输出 e 的梯度。以下情况非常简单:

然而,为了确定 a 和 b 的梯度,我们需要应用链式法则。
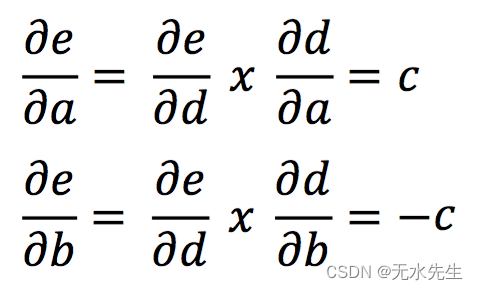
并且,通过简单地将节点输入的梯度与该节点输出的梯度相乘来计算梯度。如果你还是一头雾水,只要仔细看5遍方程式你就明白了!
但实际案例并没有那么简单。我们再举一个例子。考虑将单个输入输入到下一层中的多个项目的情况,因为神经网络几乎总是这种情况。
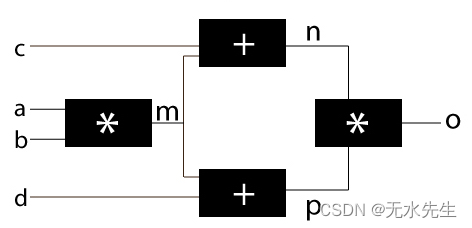
在这种情况下,除了“m”之外,所有其他的梯度将与上面的示例非常相似,因为 m 被馈送到 2 个节点中。在这里,我将展示如何确定 m 的梯度,其余的你应该自己计算。

在这里你可以看到梯度只是两个不同梯度的总和。我希望乌云正在慢慢消失,一切都变得清晰。只要理解这些概念,我们就会回到这个话题。
在继续之前,让我们总结一下神经网络优化背后的整个过程。每次迭代涉及的各个步骤是:
- 选择网络架构,即隐藏层数、每层神经元数和激活函数
- 随机初始化权重
- 使用前向传播来确定输出节点
- 使用已知标签找出模型的误差
- 将误差反向传播到网络中并确定每个节点的误差
- 更新权重以最小化梯度
到目前为止,我们已经介绍了#1 – #3,并且对#5 有了一些直觉。现在让我们从#4 – #6 开始。我们将使用第 4 节中描述的相同的 NN 通用结构。
#4-找出错误
e L (i) = y (i) - a L (i) | e L (i) = y (i) - a L (i) | i = 1,2,...,N L这里 y (i)是训练数据的实际结果
#5-将误差反向传播到网络中
L-1 层的误差应首先使用以下公式确定:
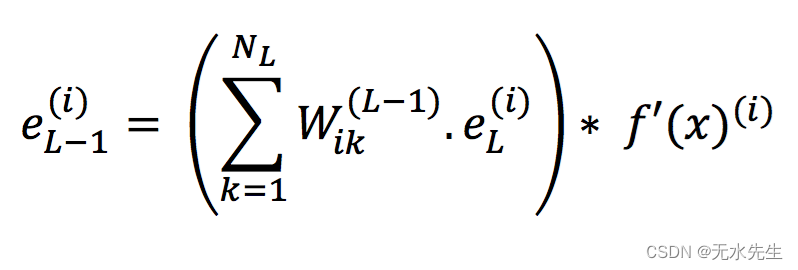
其中 i = 0,1,2, ….., NL-1(L-1 层的节点数)
从本节前半部分讨论的概念中得到的直觉:
- 我们看到一个节点的梯度是下一层所有节点梯度的函数。这里,节点的误差基于下一层所有节点的误差的加权和,该下一层的所有节点将该节点的输出作为输入。由于误差是使用每个节点的梯度计算的,因此该因素就出现了。
- f'(x) (i)是指进入该节点的输入的激活函数的导数。请注意,x 是指应用激活函数之前当前节点中所有输入的加权和。
- 这里遵循链式法则,将当前节点的梯度(即 f'(x) ( i )) 与来自方程 RHS 前半部分的后续节点的梯度相乘。
这个过程必须从L-1层到第2层连续重复。请注意,第一层只是输入。
#6-更新权重以最小化梯度
使用以下权重更新规则:Wik (l) = Wik (l) + a (i) .el + 1 (k)这里,
- l = 1,2,….., (L-1) | 层索引(不包括最后一层)
- i = 0,1,….., N l | 第l层节点索引
- k = 1,2,…., N l+1 | 第l+ 1层节点索引
- Wik (l)指第i个节点到第k个节点第l层到第l+1层的权重
我希望公约是明确的。我建议您多次查看,如果仍有疑问,我很乐意通过下面的评论来解答。
至此,我们已经成功地理解了神经网络的工作原理。如有需要,欢迎进一步讨论。
八、经常问的问题
A. 深度学习的基础包括:
1. 神经网络:深度学习依赖于人工神经网络,人工神经网络由互连的人工神经元层组成。
2.深层:深度学习模型具有多个隐藏层,使它们能够学习数据的层次表示。
3. 使用反向传播进行训练:深度学习模型是使用反向传播进行训练的,反向传播根据前向和反向传播过程中计算的误差来调整模型的权重。
4. 激活函数:激活函数将非线性引入网络,使其能够学习复杂的模式。
5. 大型数据集:深度学习模型需要大型标记数据集才能有效地从数据中学习和概括。
A. 神经网络的基本原理包括:
1. 神经元:神经网络由模仿生物神经元行为的互连人工神经元组成。
2.权重和偏差:神经元具有相关的权重和偏差,决定它们的连接强度和激活阈值。
3. 激活函数:每个神经元对其输入应用激活函数,引入非线性并实现复杂的计算。
4. 层:神经元被组织成层,包括输入层、隐藏层和输出层,用于处理和转换数据。
5.反向传播:使用反向传播来训练神经网络,根据误差梯度调整权重以提高性能。
九、后记
本文重点介绍神经网络的基础知识及其工作原理。我希望现在您了解神经网络的工作原理,并且永远不会将其用作黑匣子。一旦你了解并实际操作起来,这真的很容易。
因此,在我即将发表的文章中,我将解释在 Python 中使用神经网络的应用。除了理论之外,我将重点关注神经网络的实践方面。我立即想到了两个应用程序:
- 图像处理
- 自然语言处理
我希望你喜欢这个。如果您能通过下面的评论分享您的反馈,我会很高兴。期待与您就此进一步交流!
https://www.analyticsvidhya.com/blog/2016/03/introduction-deep-learning-fundamentals-neural-networks/









![[C++ 从入门到精通] 12.重载运算符、赋值运算符重载、析构函数](https://img-blog.csdnimg.cn/c8c28b68ad7e4cffad173c33a2097759.png)