Transformers are RNNs: Fast Autoregressive Transformers with Linear Attention
公众号:EDPJ(进 Q 交流群:922230617 或加 VX:CV_EDPJ 进 V 交流群)
![]()
目录
0. 摘要
3. 线性 Transformers
3.1. Transformer
3.2. 线性注意力机制
3.2.1. 特征映射与计算成本
3.3. 因果掩码
3.3.1. 梯度计算
3.3.2. 训练和推理
3.4. transformer 是 RNN
4. 实验
0. 摘要
Transformer 在多项任务中表现出色,但由于其对输入长度的二次复杂度,对于非常长的序列来说,速度极慢。为了解决这一限制,我们将自注意力表示为核特征映射(kernel feature maps)的线性点积,并利用矩阵乘积的结合性将复杂度从 O(N^2) 降低到 O(N),其中 N 是序列长度。我们证明了这种表达方式允许一种迭代实现,大大加速了自回归 Transformer,并揭示了它们与递归神经网络的关系。我们的线性 Transformer 在性能上与普通 Transformer 相似,并且在非常长序列的自回归预测中速度快达 4000 倍。
3. 线性 Transformers
在本节中,我们提出了线性 Transformer。我们展示了将传统的 softmax 注意力机制改为基于特征映射的点积注意力,可以改善时间和内存复杂度,并且可以实现类似于 RNN 的线性时间序列生成模型。
3.1. Transformer
![]()
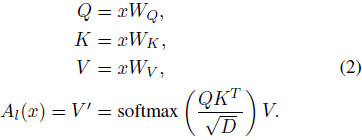
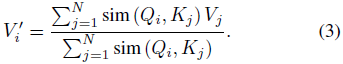
![]()
3.2. 线性注意力机制
公式 2 中的注意力定义是通用的,可以用于定义多种其他注意力实现,例如多项式注意力或 RBF 核注意力(Tsai等人,2019)。注意,为了使公式 3 定义的注意力函数有效,我们需要对 sim(·) 施加的唯一约束是非负性。这包括所有核函数 k(x, y): R^(2 × F) → R_+。
给定具有特征表示 ϕ(x) 的核函数,我们可以将公式 2 重写为:
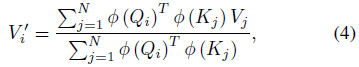
然后利用矩阵乘法的结合性进一步简化为:
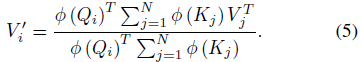
当分子以向量形式书写时,上述公式更容易理解,如下所示:
![]()
注意,特征映射 ϕ(·) 是逐行应用于矩阵 Q 和 K 的。
从公式 2 可以看出,softmax 注意力的计算成本随 O(N^2) 缩放,其中 N 表示序列长度。内存需求也是如此,因为必须存储完整的注意力矩阵以计算查询、键和值的梯度。相比之下,我们在公式 5 中提出的线性 transformer 具有 O(N) 的时间和内存复杂度,因为我们可以计算
![]()
一次,并在每个查询中重复使用它们。
3.2.1. 特征映射与计算成本
对于 softmax 注意力,就乘法和加法的总成本而言,随着 O(N^2·max(D, M)) 缩放,其中 D 是查询和键的维度,M 是值的维度。相反,对于线性注意力,我们首先计算维度为 C 的特征映射。随后,计算新值需要 O(NCM) 次加法和乘法。
上述分析未考虑核函数和特征函数的选择。需要注意的是,对应于指数核的特征函数是无限维的,这使得精确 softmax 注意力的线性化不可行。另一方面,例如多项式核具有精确的有限维特征映射,并且已证明与指数或 RBF 核(Tsai等人,2019)同样有效。线性化多项式 transformer 的计算成本为 O(N·D^2·M)。当 N > D^2 时,这使得计算复杂度更具优势。实际上,由于我们希望能够处理成千上万元素的序列,这一情况是成立的。
对于我们的实验,处理较小的序列,我们采用了一个结果为正相似函数的特征映射,如下定义:
![]()
其中 elu(·) 表示指数线性单元(Clevert等人,2015)的激活函数。我们更喜欢 elu(·) 而不是relu(·),以避免在 x 为负时将梯度设置为 0。这种特征映射导致的注意力函数需要 O(NDM) 次乘法和加法。在我们的实验部分,我们展示了公式 7 的特征映射在性能上与完整 transformer 相当,同时显著减少了计算和内存需求。
3.3. 因果掩码
transformer 架构可以通过掩蔽(masking)注意力计算来高效地训练自回归模型,使得第 i 个位置只能被第 j 个位置影响当且仅当 j ≤ i,即一个位置不能被后续位置影响。形式上,这种因果掩码将公式 3 修改如下:
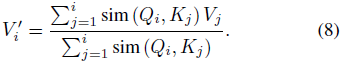
按照3.2节的推理,我们如下所述对掩码注意力进行线性化:
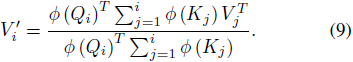
通过引入 Si 和 Zi 如下所示:
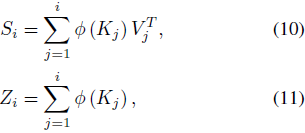
我们可以将公式 9 简化为:
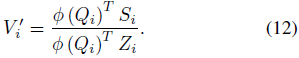
注意,Si 和 Zi 可以从 S_(i-1) 和 Z_(i-1) 在固定时间内计算得出,因此使得具有因果掩码的线性 transformer 的计算复杂度相对于序列长度为线性。
3.3.1. 梯度计算
在任何深度学习框架中,公式 12 的朴素实现需要存储所有中间值 Si,以计算梯度。这会增加max(D, M) 倍的内存消耗,从而阻碍因果线性注意力在更长序列或更深模型中的应用。为了解决这个问题,我们将公式 9 中的分子(numerator)的梯度导出为累积和。这使我们能够在线性时间和固定内存中计算因果线性注意力的前向和后向传播。详细推导见附录材料。
给定分子 ¯V_i 和标量损失函数相对于分子的梯度
![]()
推导可得:
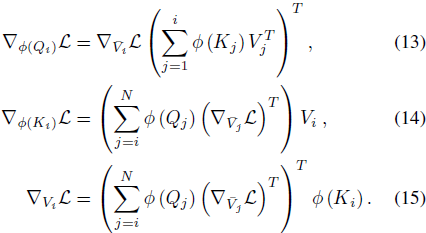
累计和项在公式 9 和 13-15 中以线性时间计算,并且相对于序列长度需要常量内存。这导致的算法在给定维度为 C 的特征映射下,其计算复杂度为 O(NCM),内存复杂度为 O(N·max (C, M))。算法 1 是分子部分前向和后向传播的伪代码实现。

3.3.2. 训练和推理
在训练自回归 transformer 模型时,可以使用完整的真实序列。这使得公式 1 中的函数 φ(·) 和注意力计算都可以进行分层并行化。因此,transformer 比 RNN 更高效地进行训练。然而,在推理过程中,时间步 i 的输出是时间步 i + 1 的输入。这使得自回归模型无法并行化。此外,transformer 每个时间步的成本不是常量,而是随着当前序列长度的平方增长,因为必须为所有先前的时间步计算注意力。
我们提出的线性 transformer 模型结合了这两者的优点。在训练时,计算可以并行化并充分利用 GPU 或其他加速器。在推理时,我们模型的每次预测在时间和内存上的成本是常量的。这意味着我们可以简单地将
![]()
矩阵存储为内部状态,并在每个时间步像递归神经网络一样更新它。这使得推理速度比其他 transformer 模型快数千倍。
3.4. transformer 是 RNN
在文献中,transformer 模型被认为是一种与递归神经网络(RNN)根本不同的方法。然而,从 3.3 节中的因果掩码公式和前一节的讨论可以看出,任何具有因果掩码的 transformer 层都可以被表示为一种模型,该模型在给定输入后修改内部状态,然后预测输出,即 RNN。注意,与通用变压器(Universal Transformers)(Dehghani等人,2018)不同,我们考虑的是时间上的递归,而不是深度上的递归。
在以下公式中,我们将公式 1 的 Transformer 层形式化为 RNN。所得的 RNN 有两个隐藏状态,即注意力记忆 s 和归一化记忆 z。我们用下标表示递归中的时间步。
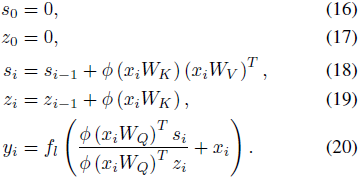
在上述公式中,x_i 表示特定 Transformer 层的第 i 个输入,y_i 表示第 i 个输出。需要注意的是,我们的公式对特征函数没有任何约束,因此可以用于表示任何 Transformer 模型,理论上甚至包括使用 softmax 注意力的模型。这一公式是更好理解 Transformer 与流行的 RNN(Hochreiter & Schmidhuber, 1997)及其存储和检索信息过程之间关系的第一步。
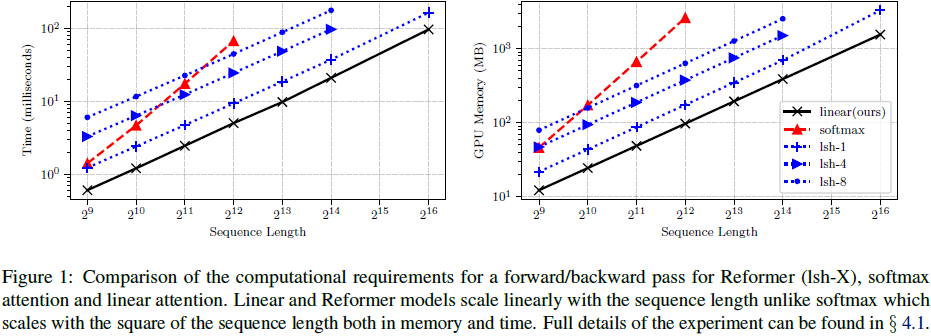
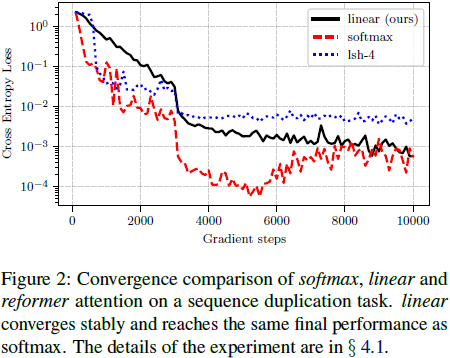
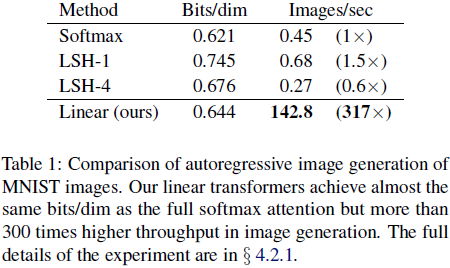
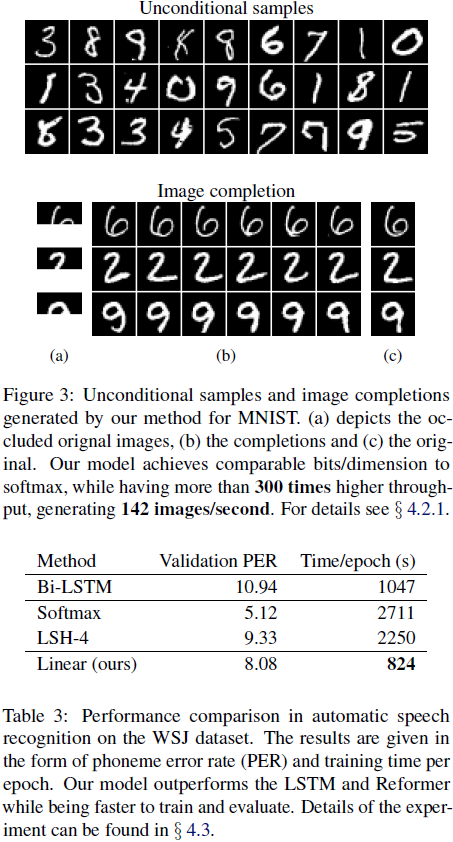
4. 实验







![[9] CUDA性能测量与错误处理](https://img-blog.csdnimg.cn/direct/9035a7e438f946769e9df195c25096c4.png)