本文针对以下几个方面问题进行整理:
- 最短路问题
- 两个指定顶点之间的最短路径
- 任意顶点之间的最短路径
2.最小生成树问题
- 求最小生成树
3.网络最大流问题
- 源点与汇点之间的最大流
- 基于最大流的最小费用求解
4.旅行商问题
- 基于哈密顿(Hamilton)圈求解旅行商线性规划
最短路问题:
两个指定点最小距离:
%使用graphshortestpath函数
[dist, path, pred]=graphshortestpath(G,S,T)G是稀疏矩阵,S是起点,T是终点。dist表示最短距离,path表示最短距离经过的路径节点,pred表示从S到每个节点的最短路径中,目标节点的先驱,即目标节点的前面一个节点。比如一共有6个点,S=1,那么运行这个函数后pred存的就是S=1这个节点到其它节点T'最短路径上T'的前一个节点。这个函数也就是求出图G上S到T的[dist, path, pred],当不写T时表示求S到其它所有点的[dist, path, pred]。
任意顶点的最短路径:
!使用graphallshortestpath函数
[dist] = graphallshortestpaths(G)- 解题思路:

简单构造稀疏矩阵:
- 手动录入权重矩阵
!w(起点,终点)=权重值
w=zeros(4)
w(1,2)=2;w(1,3)=3;w(1,4)=8;
w(2,3)=6;w(2,4)=6;
G=sparse(w);
%如果是无向图,G=sparse(tril(w'+w)取下三角)得:
G =
(1,2) 2
(1,3) 3
(2,3) 6
(1,4) 8
(2,4) 6
2. 直接sparse函数生成
%sparse([起点集合],[对应终点集合],[对应权重集合])
G=sparse([1,1,2,1,2],[2,3,3,4,4],[2,3,6,8,6]);
%得到结果和上面相同
%如果是无向图,建议用方法1对无向图而言:tril(w+w')是在不知道w是上三角还是下三角的情况下,确保取w对应的下三角;若w已知为上三角,稀疏矩阵G=sparse(w');若已知w为下三角,稀疏矩阵G=sparse(w);
例题:某公司在六个城市c1,c2,..c6中有分公司,从ci(1..6)到cj(1..6)的距离c(i,j)记在下述矩阵中,求ci到其他城市的最短距离。
| 0 | 50 | ∞ | 40 | 25 | 10 |
|---|---|---|---|---|---|
| 50 | 0 | 15 | 20 | ∞ | 25 |
| ∞ | 15 | 0 | 10 | 20 | ∞ |
| 40 | 20 | 10 | 0 | 10 | 25 |
| 25 | ∞ | 20 | 10 | 0 | 55 |
| 10 | 25 | ∞ | 25 | 55 | 0 |
clear;
clc;
w=zeros(6);
w(1,2)=50;w(1,4)=40;w(1,5)=25;w(1,6)=10;
w(2,3)=15;w(2,4)=20;w(2,6)=25;
w(3,4)=10;w(3,5)=20;
w(4,5)=10;w(4,6)=25;
w(5,6)=55;
%无向图
G=sparse(w');
a=graphallshortestpaths(G,'Direct',0)
%记住要加Direct 0/false 说明是无向图 1/true则为有向图得:
a =
0 35 45 35 25 10
35 0 15 20 30 25
45 15 0 10 20 35
35 20 10 0 10 25
25 30 20 10 0 35
10 25 35 25 35 0
例如第一行表示c1到ci(1..6)最短距离分别为[0,35,45,35,25,10].
最小生成树问题
同样直接运用graphminspantree函数并加一些图形显示参数即可
例:北京(Pe)、东京(T)、纽约(N)、墨西哥城(M)、伦敦(L)、巴黎(Pa)各城市之间航线距离如下表
| L | M | N | Pa | Pe | T | |
|---|---|---|---|---|---|---|
| L | 56 | 35 | 21 | 51 | 60 | |
| M | 56 | 21 | 57 | 78 | 70 | |
| N | 35 | 21 | 36 | 68 | 68 | |
| Pa | 21 | 57 | 36 | 51 | 61 | |
| Pe | 51 | 78 | 68 | 51 | 13 | |
| T | 60 | 70 | 68 | 61 | 13 |
求由上述交通网络数据确定的最小生成树:
clc, clear
a=zeros(6); %邻接矩阵初始化
a(1,[2:6])=[56 35 21 51 60]; %输入邻接矩阵的上三角元素
a(2,[3:6])=[21 57 78 70];
a(3,[4:6])=[36 68 68];
a(4,[5 6])=[51 61]; a(5,6)=13;
a=a'; a=sparse(a); %变换成下三角矩阵,并转化成工具箱所需要的稀疏矩阵
[ST,pred] = graphminspantree(a,'method','Kruskal') %调用工具箱求最小生成树并定义用kruskal算法求解
nodestr={'L','M','N','Pa','Pe','T'}; %输入顶点名称的字符细胞数组
h=view(biograph(ST,nodestr,'ShowArrows','on','ShowWeights','on'))%将节点名称显示在图形上,并显示箭头以及对应的权重
h.EdgeType='segmented'; %边的连接为线段
h.LayoutType='equilibrium'; dolayout(h) %设置图形布局属性,并刷新图形布局graphminspantree不需要指定Direct是0/1,但对于无向图仍然需要将输入得稀疏矩阵转为下三角矩阵。
网络最大流问题:
同样,我们只需调用graphmaxflow函数即可

求最大流:
clc,clear
a=zeros(6);
%标号s=1 v1=2 v3=3 v2=4 v4=5 t=6
a(1,2)=8;a(1,3)=7;
a(2,3)=5;a(2,4)=9;
a(3,5)=9;
%有向图 不是上三角或下三角矩阵
a(4,3)=2;a(4,6)=5;
a(5,4)=6;a(5,6)=10;
%有向图 直接取稀疏矩阵
a=sparse(a);
%1,6表示求源点s和汇点t之间的最大流
[b,c]=graphmaxflow(a,1,6)
%b返回最大流 c返回每条管道对应的流量得:
b =
14
c =
(1,2) 8.0000
(1,3) 6.0000
(2,3) 1.0000
(4,3) 2.0000
(2,4) 7.0000
(3,5) 9.0000
(4,6) 5.0000
(5,6) 9.0000
最大流最小费用问题再加上一定的约束即可,这里不再细说.
旅行商问题
旅行商问题是经典得哈密顿圈图论问题,具体可以自行百度其原理。这里给出lingo求解源码,只需带入初始矩阵即可。
约束条件:

+
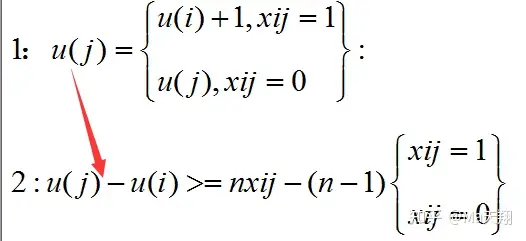
1=2 转换为不等式使程序求解速度更快
model:
sets:city / 1..10/: u;link(city, city):dist,x;
endsets n = @size(city);
data: dist = 0 8 5 9 12 14 12 16 17 228 0 9 15 17 8 11 18 14 225 9 0 7 9 11 7 12 12 179 15 7 0 3 17 10 7 15 1812 17 9 3 0 8 10 6 15 1814 8 11 17 8 0 9 14 8 1612 11 7 10 10 9 0 8 6 1116 18 12 7 6 14 8 0 11 1117 14 12 15 15 8 6 11 0 1022 22 17 18 15 16 11 11 10 0;
enddatamin = @sum(link:dist*x);@FOR(city(K):@sum(city(I)|I#ne#K:x(I,K)=1;@sum(city(J)|J#ne# K: x( K, J))=1;);@for(city(I)|I#gt#1:@for(city(J)|J#gt#1#and#I#ne#J:u(I)-u(J)+n*x(I,J)<=n-1););@for(city(I)|I#gt#1:u(I)<=n-2);@for(link:@bin(x));
end
!只需替换data中 dist的距离矩阵以及初始化条件city的维数即可总结
对于求解最小路径、最大流、最小生成树等问题使用matalab工具箱函数即可。统一的,对于有向图直接取稀疏矩阵,对于无向图需要取其下三角矩阵再求稀疏矩阵。
写了一天,累die....打球去了,希望可以帮助更多的人更好的理解和运用这些算法。如有不当,请指正。
参考书目:
数学建模算法与应用
数学模型算法与应用模型与解答