avl树中insert的模拟实现
avl树特点:
1.是搜索二叉树
2.每个结点的左右子树高度差的绝对值不超过2
inser模拟实现:
// 右单旋void RotateR(Node* pParent){Node* parent = pParent;Node* pr = parent->_pRight;Node* prl = pr->_pLeft;//记录父节点Node* pp = parent->_pParent;//更新指针parent->_pRight = prl;if(prl)//判断prl是否存在prl->_pParent = parent;pr->_pLeft = parent;parent->_pParent = pr;if (pp == nullptr){//若parent是根节点_pRoot = pr;pr->_pParent = nullptr;}else{ //父节点连接if (pp->_data < parent->_data){pp->_pRight = pr;pr->_pParent = pp;}else{pp->_pLeft = pr;pr->_pParent = pp;}}//更新平衡因子parent->_bf = 0;pr->_bf = 0;}// 左单旋void RotateL(Node* pParent){Node* parent = pParent;Node* pl = parent->_pLeft;Node* plr = pl->_pRight;//记录父节点Node* pp = parent->_pParent;//更新指针parent->_pLeft = plr;if (plr)//判断prl是否存在plr->_pParent = parent;pl->_pRight = parent;parent->_pParent = pl;if (pp == nullptr){//若parent是根节点_pRoot = pl;pl->_pParent = nullptr;}else{ //父节点连接if (pp->_data < parent->_data){pp->_pRight = pl;pl->_pParent = pp;}else{pp->_pLeft = pl;pl->_pParent = pp;}}//更新平衡因子parent->_bf = 0;pl->_bf = 0;}// 右左双旋void RotateRL(Node* pParent){ Node* parent = pParent;Node* pr = parent->_pRight;Node* prl = pr->_pLeft;int bf = prl->_bf;RotateL(pParent->_pRight);RotateR(pParent);//更新平衡因子if (bf == 0){parent->_bf = pr->_bf = prl->_bf = 0;}else{parent->_bf = -1;pr->_bf = prl->_bf = 0;}}// 左右双旋void RotateLR(Node* pParent){Node* parent = pParent;Node* pl= parent->_pLeft;Node* plr = pl->_pRight;int bf = plr->_bf;RotateR(pParent->_pLeft);RotateL(pParent);//更新平衡因子if (bf == 0){parent->_bf = pl->_bf = plr->_bf = 0;}else{parent->_bf = 0;pl->_bf = 1;plr->_bf = 0;}}// 在AVL树中插入值为data的节点bool Insert(const T& data){if (_pRoot == nullptr){_pRoot = new Node(data);return true;}Node* cur = _pRoot;Node* parent = nullptr;//查看插入位置while (cur){if (cur->_data < data){ parent = cur;cur = cur->_pRight;}else if (cur->_data > data){ parent = cur;cur = cur->_pLeft;}else{//有重复值,插入失败return false;}}//此时parent的子树就是存放data的结点if (parent->_data < data){cur = new Node(data);parent->_pRight = cur;cur->_pParent = parent;parent->_bf++;}else{cur = new Node(data);parent->_pLeft = cur;cur->_pParent = parent;parent->_bf--;}//开始旋转while (parent){if (parent->_bf == 0){//代表插入前后高度不变break;}else if (parent->_bf == 1 || parent->_bf == -1){//插入后高度改变,但仍保持平衡条件cur = parent;parent = parent->_pParent;if (parent == nullptr){break;}if (cur == parent->_pLeft){parent->_bf--;}else{parent->_bf++;}}else if (parent->_bf == 2 || parent->_bf == -2){//此时不满足平衡条件,需要旋转//旋转分四种情况//1.右右if(parent->_bf==2&&cur->_bf==1)RotateR(parent);//2。左左else if(parent->_bf == -2 && cur->_bf == -1)RotateL(parent);//3.右左else if(parent->_bf == 2 && cur->_bf == -1)RotateRL(parent);//4.左右else if(parent->_bf == -2 && cur->_bf == 1)RotateLR(parent);//旋转后高度和插入前高度相同,因此结束break;}else{//此时平衡因子异常,发出中断请求assert(false);}}}对于一个结点的插入,其影响其父节点的平衡因子(_bf)的值,因此每次插入都需要修改其父节点的平衡因子,而父节点的平衡因子的修改又可能会影响父节点的父节点的平衡因子的值,因此可能会出现连锁修改的情况。以下是所有可能的情况:
1.插入结点后父节点的平衡因子的值变为0,在该情况下父节点的高度在插入前后未发生改变,因此不会继续影响父节点的父节点,因此可以直接退出循环。
2.插入结点后父节点的平衡因子的值变为1或-1,在该情况下父节点的高度插入前后发生修改,增加1,此处通过判断父节点是其父节点的左右子树,来影响父节点的父节点的平衡因子,并继续进入循环进行判断。
3。插入后父节点平衡因子变成大于2的情况,此时抛出异常,因为父节点的平衡因子应符合不超过2,即使在插入新节点后,其平衡因子最大只能增加1,最小只能减小1,因此只能变成绝对值小于等于2的情况,不应该出现绝对值大于2的情况。
3.插入结点后父节点平衡因子变成2或-2,此时不在符合平衡因子绝对值不超过2的情况,因此需要对以父节点为根结点的子树进行旋转修改。此时又分成四种情况。
情况1:

对于这种情况,只需要进行一次选择即可,旋转后的结果如下图:

具体实现逻辑就是parent变成其右孩子的左孩子,原本右孩子的左孩子变成parent的右孩子
经过旋转,使得当前的二叉树仍是avl树,其旋转后的高度与插入结点之前的高度一致,因此不需要继续向上修改父节点。
情况2:

此时若只以A为根进行旋转,则旋转后仍有平衡因子为2或-2的情况,因此需要进行两次旋转。为方便理解,上图等价于下图,以下图来分析。

具体思路:先以b为根进行旋转,使得旋转后高度更高的结点在右侧。
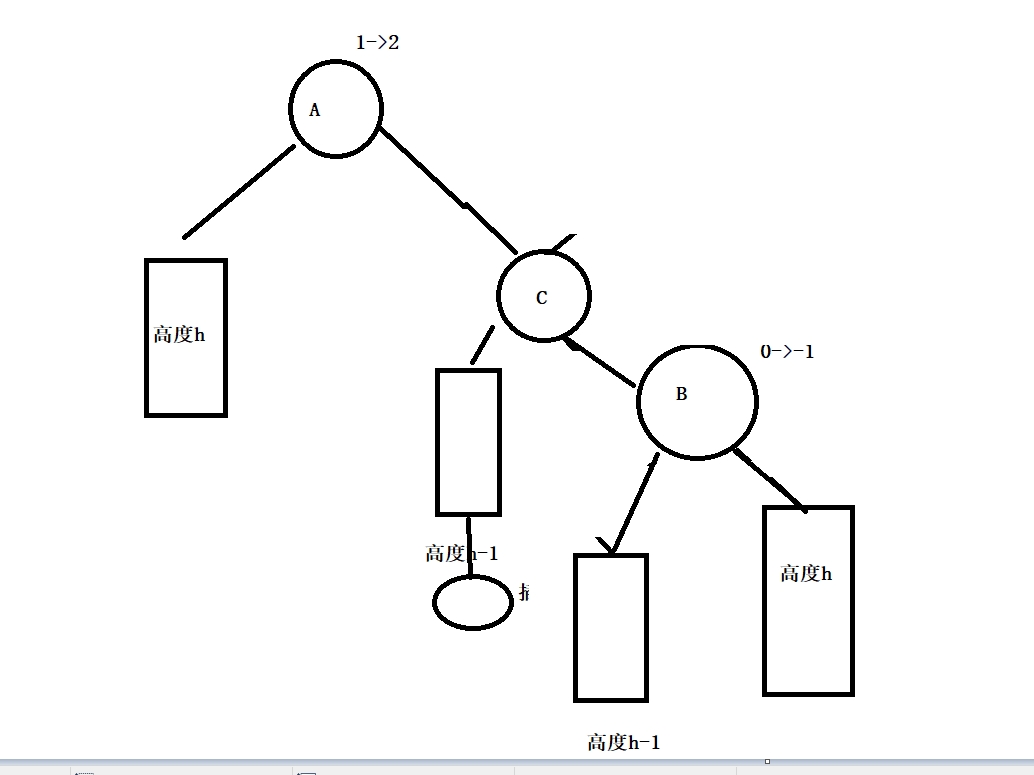
然后以A为根进行旋转即可。
经过两次旋转,实现了高度缩减一,且和插入结点之前相比,子树的父节点的平衡因子不用改变,因此也不需要继续进入循环。
对于上述两种情况,存在镜像的情况,对于那两种情况,只需要与对应的将左右旋转、子树旋转等改变即可。