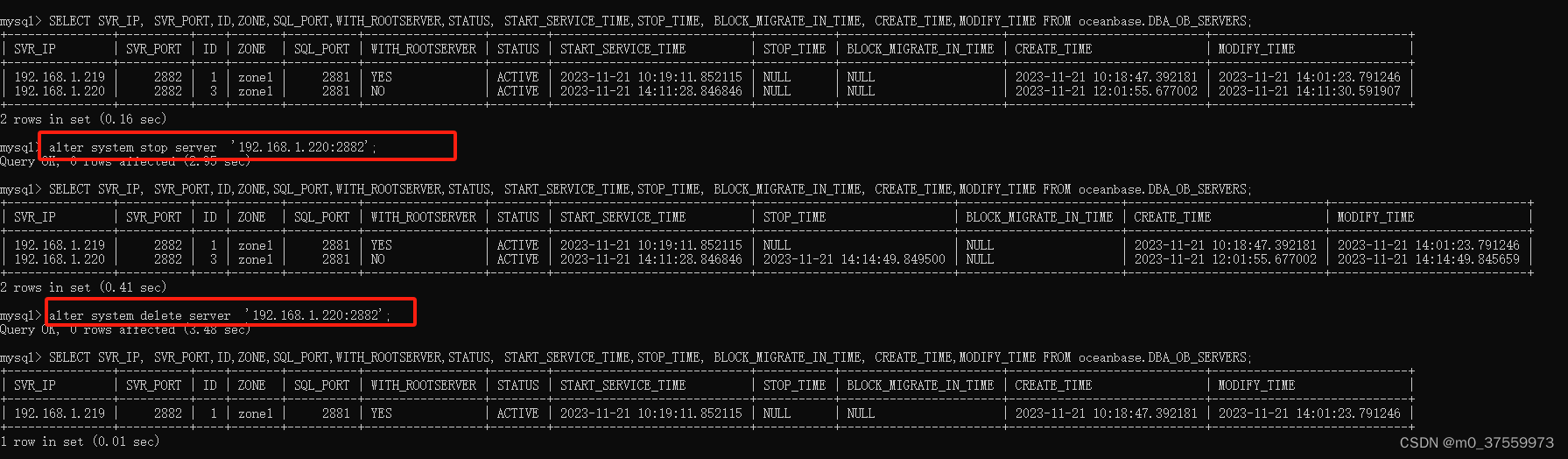
如图为某一状态下 x 轴上的情况,此时 E、F相距最远,现在加入一个点H,如果H位于点A的左边的话,只需要比较 A、H 的距离 和 E、F 的距离;如果点H位于点G的右边,则值需要比较 G、H 的距离 和 E、F 的距离;如果点H位于点 E、F 之间就比较难搞了,因为此时点 E、F被分开了,而且点 E、H的距离 和 点 H、F 的距离都不一定是最大的,所以算法还需要维护一个相距第二远的两个点,比如图中点 D、E 相距第二远,当点H位于点EF之间时,取点E、H的距离和点 H、F的距离的最大值,记作 max{ EH,HF },让 max{ EH,HF } 和 DE 比较已确定最大距离并更新最大距离和第二大距离;如果点H位于其他位置,即图中 A、B 之间,B、C 之间, C、D 之间, D、E 之间, F、G 之间,都不会产生更大的距离,因为这些距离本来就没有最大距离 EF大,现在又被从中分开了;所以给予以上的分析,动态规划的过程中不仅要维护最大距离的两个点,还要维护点A、点G这两个最小值点和最大值点,还要维护第二大距离的两个点。