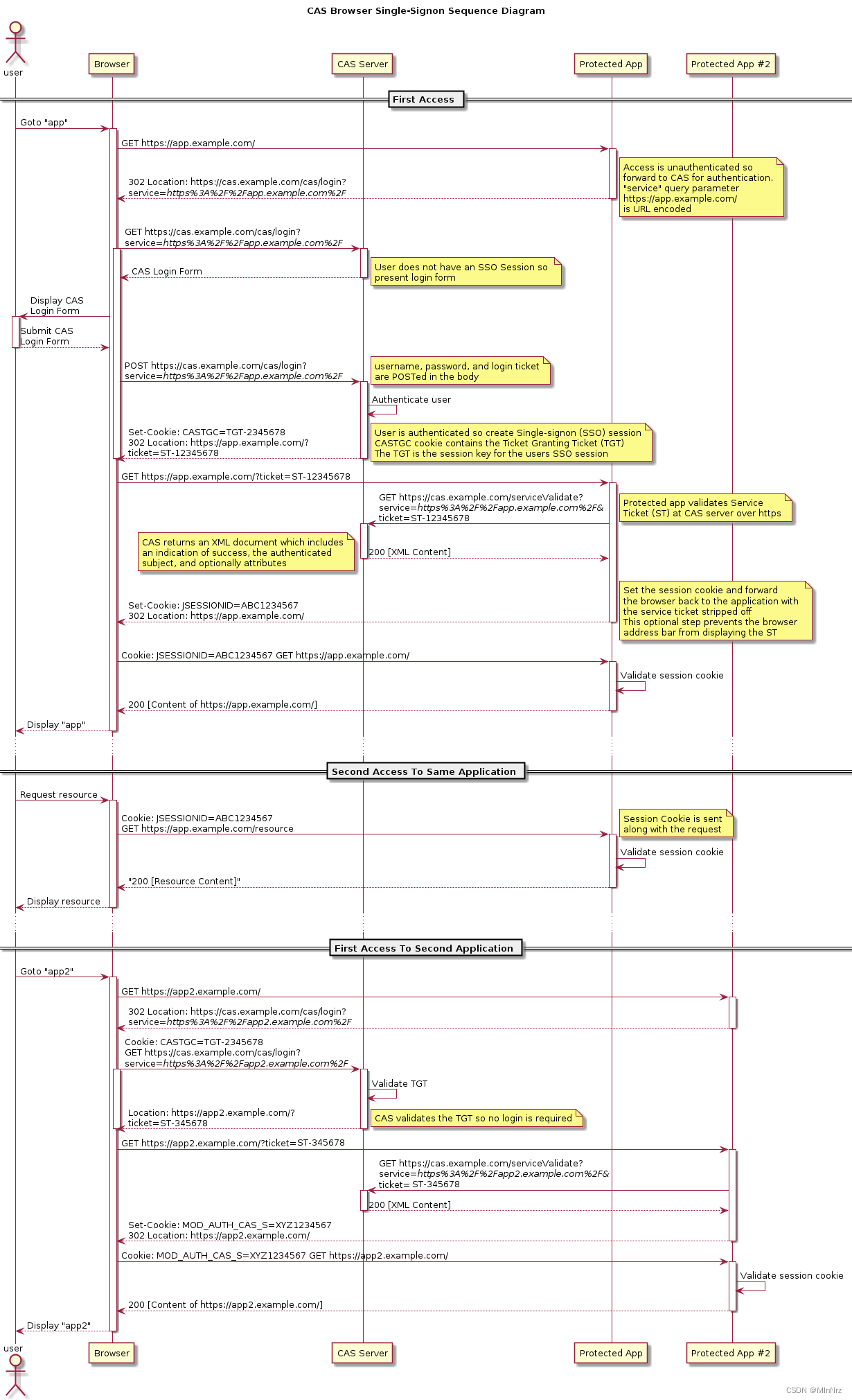
文章目录
- 1. rotation matrix
- 1.1 结论
- 2. reflection matrix
- 2.1 结论
1. rotation matrix
图像逆时针旋转 θ \theta θ的矩阵
Q r o t a t e = [ cos θ − sin θ sin θ cos θ ] (1) Q_{rotate}=\begin{bmatrix}\cos\theta&-\sin\theta\\\sin\theta&\cos\theta\end{bmatrix}\tag1 Qrotate=[cosθsinθ−sinθcosθ](1)
- 为了方便计算和表达,我们用 I I I单位矩阵进行分析
I = [ 1 0 0 1 ] (2) I=\begin{bmatrix}1&0\\0&1\end{bmatrix}\tag2 I=[1001](2)
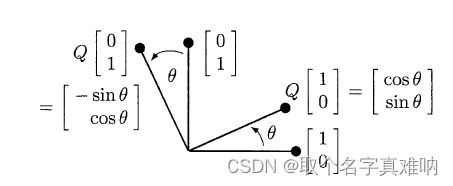
可以得到两个点 Q=(1 , 0);Q=( 0, 1),我们将两个向量逆时针旋转 θ \theta θ角度后,可以得到此时的角度
Q ′ [ 1 , 0 ] = [ cos θ sin θ ] (3) Q'[1,0]=\begin{bmatrix}\cos\theta\\\sin\theta\end{bmatrix}\tag3 Q′[1,0]=[cosθsinθ](3)
Q ′ [ 0 , 1 ] = [ − sin θ cos θ ] (4) Q'[0,1]=\begin{bmatrix}-\sin\theta\\\cos\theta\end{bmatrix}\tag4 Q′[0,1]=[−sinθcosθ](4)
所以可以得到 I I I单位向量在逆时针旋转 θ \theta θ后的旋转矩阵如下
1.1 结论
Q r o t a t e = [ cos θ − sin θ sin θ cos θ ] (5) Q_{rotate}=\begin{bmatrix}\cos\theta&-\sin\theta\\\sin\theta&\cos\theta\end{bmatrix}\tag5 Qrotate=[cosθsinθ−sinθcosθ](5)
2. reflection matrix
Q r o t a t e = [ cos θ − sin θ sin θ cos θ ] (6) Q_{rotate}=\begin{bmatrix}\cos\theta&-\sin\theta\\\sin\theta&\cos\theta\end{bmatrix}\tag6 Qrotate=[cosθsinθ−sinθcosθ](6)
图像沿着直线 1 2 θ \frac{1}{2}\theta 21θ对称矩阵,反射矩阵
- 为了方便计算和表达,我们用 I I I单位矩阵进行分析
I = [ 1 0 0 1 ] (7) I=\begin{bmatrix}1&0\\0&1\end{bmatrix}\tag7 I=[1001](7)
可以得到两个点 Q=(1 , 0);Q=( 0, 1),我们将两个向量关于 1 2 θ \frac{1}{2}\theta 21θ直线对称后,可以得到此时的坐标
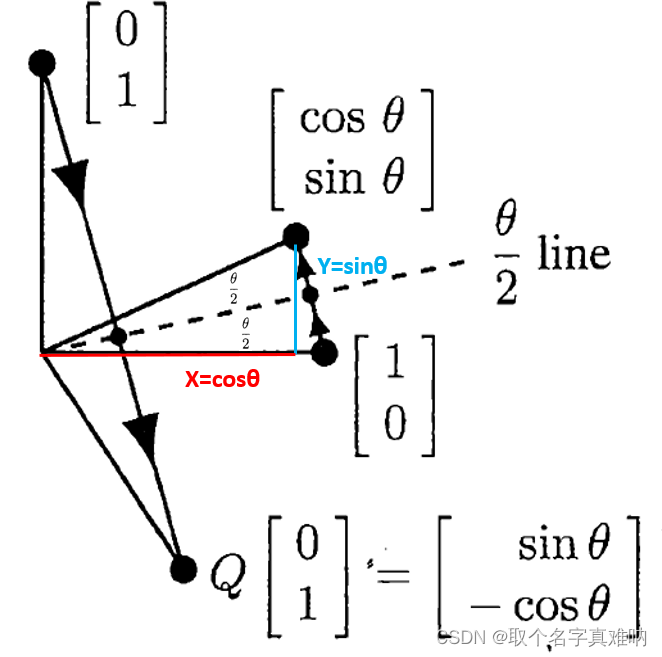
Q ′ [ 1 , 0 ] = [ cos θ sin θ ] (8) Q'[1,0]=\begin{bmatrix}\cos\theta\\\sin\theta\end{bmatrix}\tag8 Q′[1,0]=[cosθsinθ](8)
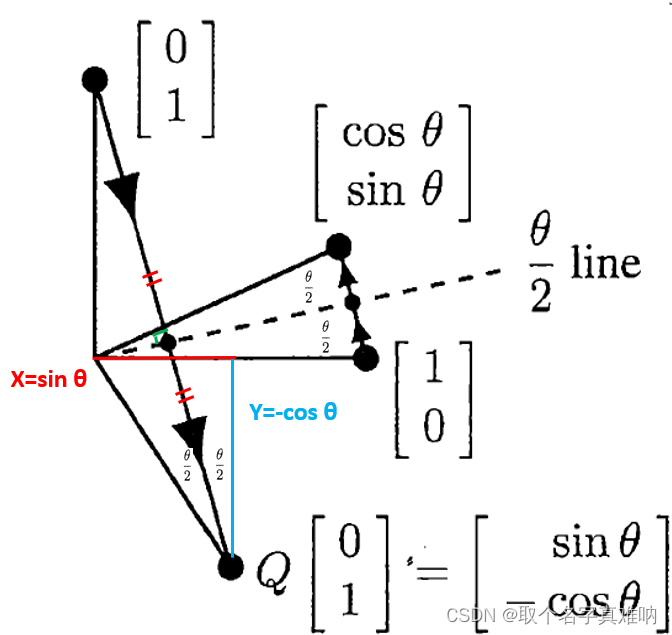
Q ′ [ 0 , 1 ] = [ sin θ − cos θ ] (9) Q'[0,1]=\begin{bmatrix}\sin\theta\\-\cos\theta\end{bmatrix}\tag9 Q′[0,1]=[sinθ−cosθ](9)
2.1 结论
Q r e f l e c t i o n = [ cos θ sin θ sin θ − cos θ ] (10) Q_{reflection}=\begin{bmatrix}\cos\theta&\sin\theta\\\sin\theta&-\cos\theta\end{bmatrix}\tag{10} Qreflection=[cosθsinθsinθ−cosθ](10)