目录
- 一、多维数组
- (一)数组的定义
- (二)二维数组
- (三)多维数组的存储
- (四)多维数组的下标的相关计算
- 二、矩阵
- (一)特殊矩阵和稀疏矩阵
- (二)对称矩阵
- (三)对角矩阵
- (四)稀疏矩阵的压缩存储
- 三、广义表
- (一)广义表的定义
- (二)广义表的表头和表尾
- (三)广义表的深度和长度
- (四)广义表表示二叉树
一、多维数组
(一)数组的定义
数组是由n(n≥1)个相同数据类型的数据元素组成的有限序列,在定义数组时,会为数组分配一个固定大小的内存空间,用来存储元素,数组在被定义后,其维度不可以被改变。
数组在确定其维度和维界后,元素的个数是固定的,所以不能进行插入和删除运算。数组中最常见的两种操作是查找和修改。
(二)二维数组
数组可分为一维数组和多维数组(常见的有二维数组),二维数组可以看作一维数组的一维数组。顺序表是一个一维数组,所以它是线性结构,与栈、队列、串的逻辑结构相同,而多维数组则是典型的非线性结构,也可以说它是嵌套的线性结构。
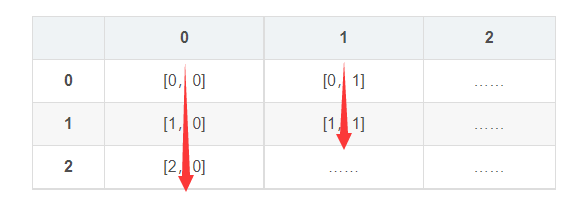
例如,一个二维数组A[3][4]在内存中实际上是一个长度为3的一维数组,每个元素是一个长度为4的一维数组,即对应三行四列,其中元素是从上到下、从左到右依次存储的,如下:
| 0 | 1 | 2 | 3 | |
|---|---|---|---|---|
| 0 | [0,0] | [0,1] | [0,2] | [0,3] |
| 1 | [1,0] | [1,1] | [1,2] | [1,3] |
| 2 | [2,0] | [2,1] | [2,2] | [2,3] |
由于数组中是从下标0开始的,所以一个m行n列的二维数组中,最开始的元素是[0,0],最后的元素是[m-1,n-1],上面三行四列的二维数组A[3][4]中的最后一个元素即为[2,3]。
(三)多维数组的存储
二维数组的存储较一维数组不一样,有两种存储方式,可分为行优先存储和列优先存储,前者是先按每行存储满后再继续下一行,后者相反先按每列存储满后再继续下一列。
例如,定义一个二维数组A[3][3],在连续的内存空间里,如下:
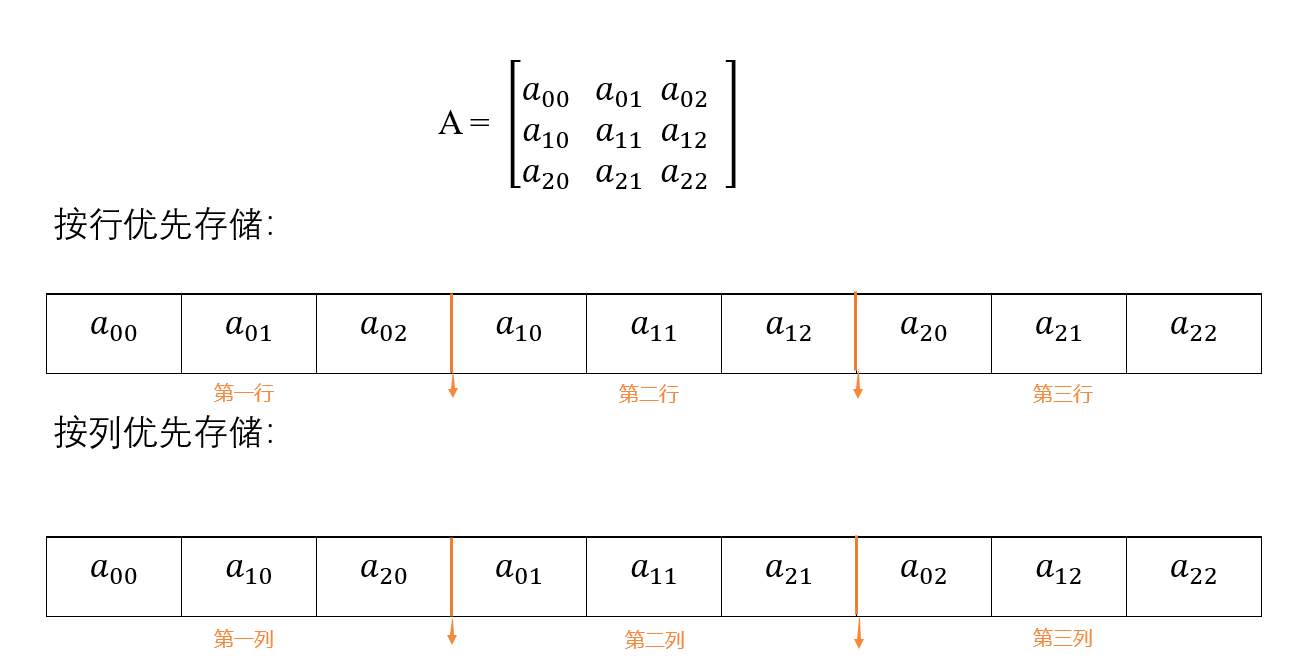
若按照行优先存储,以A[2][0]为例,在存储A[2][0]之前,是这样存储的:

而按照列优先存储,以A[1][1]为例,在存储A[1][1]之前,是这样存储的:
(四)多维数组的下标的相关计算
设一个二维数组A[i][j],其中行下标和列下标的范围分别为[0,a]和[0,b],若每个数组元素在内存中占用L个存储单元,且数组中第一个元素的存储位置为LOC[c1][c2],求该二维数组中任意一元素A[i][j]的存储位置?
1、按行优先存储
【所求行乘列界限加1,然后加所求列确定位置】
(1)先确定有多少行,加上列数,然后乘以存储单元,最后加上第一个元素的存储位置,得:LOC[i][j]=LOC[c1][c2]+[(i-c1)×(b-c2+1)+(j-c2)]×L。
(2)若在编程语言中,由于数组元素下标是从0开始的,该式子改写为:LOC[i][j]=LOC[0][0]+[i×(b+1)+j]×L。
例、二维数组A[m][n]采用行序为主方式存储,每个元素占L个存储单位。元素A[0][0]的存储地址是b,求元素A[i][j](0 ≤ i ≤ m-1,0 ≤ j ≤ n-1)的存储地址。
解析:由于二维数组中行列元素都是从0开始的,即LOC[i][j]=b+[i×(n-1+1)+j]×L=b+[i×n+j]×L。
2、按列优先存储
【所求列乘行界限加1,然后加所求行确定位置】
(1)先确定有多少列,加上行数,然后乘以存储单元,最后加上第一个元素的存储位置,得:LOC[i][j]=LOC[c1][c2]+[(j-c1)×(a-c2+1)+(j-c1)]×L。
(2)若在编程语言中,由于数组元素下标是从0开始的,该式子改写为: LOC[i][j]=LOC[0][0]+[j×(a+1)+i]×L。
例、设7行6列的数组a以列序为主序顺序存储,基地址为1024,每个元素占2个存储单元,架设无第0行第0列,求第4行第5列的元素的存储地址。
解析:由于第一个元素为a[1][1],所以要减去后再代入计算,即
LOC[4][5]=1024+[(5-1)×(7-1+1)+(4-1)]×2=1024+62=1086。
- 对于一个数组An×n(方阵),其元素aij按行优先与按列优先存储时地址之差为(n-1)(i-j)。
二、矩阵
(一)特殊矩阵和稀疏矩阵
相同的元素或零元素在矩阵中的分布存在一定规律的矩阵称为特殊矩阵,反之则为稀疏矩阵。简单的来说,特殊矩阵既然特殊,说明其中有很多相同或者有零元素,且存在一定规律在矩阵中分布。
常见的特殊矩阵有对称矩阵、反对称矩阵、上/下三角矩阵、对角矩阵等等,例如对角矩阵中,只有对角线上有元素,其余元素均为零:
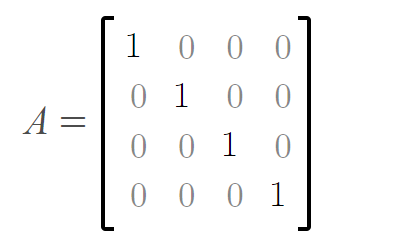
(二)对称矩阵
若一个方阵满足Ai×j=Aj×i,则称为对称矩阵。由于对称矩阵中上三角部分和下三角部分的元素对应相同,在存储对称矩阵时,为了避免空间的浪费,可以只存储上或下三角部分的元素,将其存放在一个一维数组中,该数组的大小为1+2+……+n=n(1+n)/2。
(三)对角矩阵
三对角矩阵就是一种对角矩阵,其中非零元素都集中在以主对角线为中心的三条对角线的区域中,其他区域均为零。
(四)稀疏矩阵的压缩存储
前面讲到,稀疏矩阵中非零元素的分布与特殊矩阵相反,是没有规律的。稀疏矩阵中大部分元素都为0,且与非零元素的分布一样,也是没有规律的。对矩阵压缩的目的是节省存储空间。
1、三元组表
为了压缩存储稀疏矩阵,在存储时不仅要存储矩阵中非零元素的值,同时还要存储该元素所在的行与列,从而组成一个三元组表(行、列、值),依此减少了存储空间。由于是将稀疏矩阵中的非零元素以及其对应的行、列号以三元组的形式存储在一个数组中,所以经过这种压缩存储后就无法通过数组的下标直接存取矩阵的元素,失去了随机存取的特性。另外,稀疏矩阵的三元组表也可以采用十字链表法存储。【稀疏矩阵的两种存储结构是三元组表(数组)和十字链表】
//以整型int为例,可替换其他类型
typedef struct{int i,j; //行与列int x; //值
}Sparsematrix;
例如,一个稀疏矩阵A,进行压缩存储:
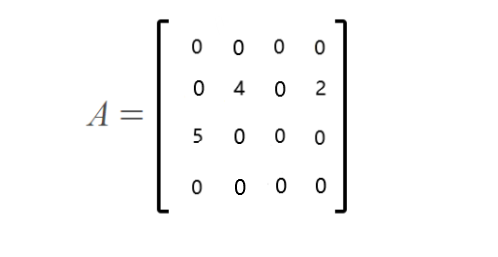
对应的三元组表,如下:
| i(行) | j(列) | x(值) |
|---|---|---|
| 1 | 1 | 4 |
| 1 | 3 | 2 |
| 2 | 0 | 5 |
例如,有一个100×90的稀疏矩阵,非0元素有10个,设每个整型数占2字节,则用三元组表示矩阵时,求所需的字节数。
解析:三元组表包括行、列、值,每个整型数占2字节,所以10个非0元素占3×2×10=60字节,另外还有三元组表中行数、列数和总的非零元素个数共6个字节,一共60+6=66字节。
2、十字链表
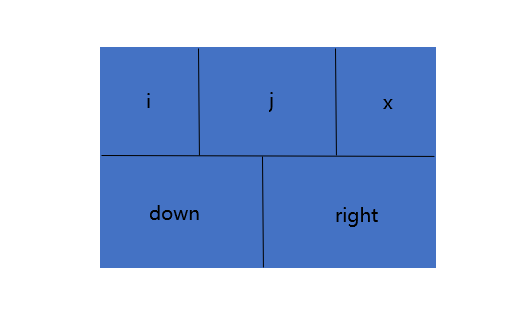
十字链表法中,稀疏矩阵的行和列都用一个带头结点的链表表示,从而对应着五个分量:行、列、数据域、指向下方结点的指针和指向右方结点的指针,其结点的结构如下:
三、广义表
(一)广义表的定义
广义表是线性表的进一步推广,是由n(n≥0)个数据元素组成的有序序列。线性表中的数据元素只能是单个元素(原子),它是不可分割的,而广义表中的数据元素既可以是原子,也可以是一个广义表(包括空表和非空表),广义表通过圆括号“()”括起来,通过逗号“,”隔开表中的各个数据元素。

一个n维数组可以看成元素是n-1维数组的广义表,广义表的元素都是n-1维数组。另外,若广义表中的所有元素都是原子时,此时的广义表就是一个线性表。
(二)广义表的表头和表尾
广义表是可以递归的,一个广义表也可以是其自身的子表,广义表中的第一个元素称为广义表的表头,而剩余数据元素组成的表称为广义表的表尾,广义表的表头和表尾可以看作通过函数Head()和Tail()对广义表操作。任何一个非空广义表,表头可能是单个元素(原子)或广义表,但表尾只可能是广义表,其原因是广义表的取表尾Tail()是非空广义表除去表头元素后,剩余元素组成的表,所以不可能是原子。
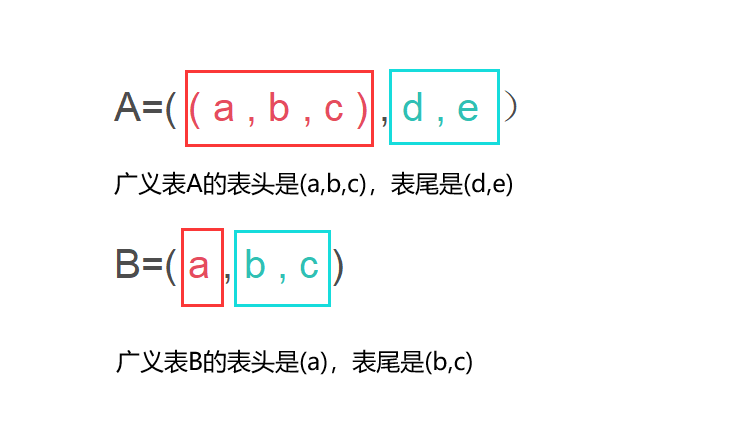
例如,C=(a,b,c,d,e,f,g),该广义表的表头是(a),表尾是(b,c,d,e,f,g);
例如,D=((a,b),((c,d,e),(f,g,h))),该广义表的表头是(a,b),表尾是((c,d,e),(f,g,h))。
另外,若一个广义表为空,则为一个空表。例如,E=( ),F=(( )),广义表E是一个空表,只有非空广义表才能取表头,广义表F的表头和表尾都是()。
(三)广义表的深度和长度
- 广义表的深度通过
括号的层数求得,而长度是广义表中所含元素的个数。
例如,一个空广义表G=(),括号层数为1,所以广义表的深度为1,而由于是空表,所以广义表的长度为0;
例如,一个广义表H=((a,b),(c,(d,e))),括号层数为3,所以广义表的深度为3,最高层为(c,(d,e)),逗号隔开了原子( c )和广义表( d,e ),元素个数为2,所以广义表的长度为2。
例如,一个广义表I=((),(a),(b,c,(d),((d,f)))),由于括号的最大层数为4,所以广义表的深度为4,可知广义表有三个元素,分别是()、(a)、(b,c,(d),((d,f))),元素个数为3,所以广义表的长度为3。
例如,设广义表J=(( ),( )),对广义表J,head(J)=( ),Tail(J)=(( )),括号的最大层数为2,所以广义表的深度为2,广义表有两个元素,分别是()、(),元素个数为2,所以广义表长度为2。
注:这里的Tail(J)=(( )),而不是( )。
(四)广义表表示二叉树
根据广义表中“ 数据元素既可以是原子,也可以是一个广义表(包括空表和非空表) ”这一点可以来表示二叉树,即通过(根结点,根结点的广义表)的形式来表示,其中可以嵌套。
例如,下面是一个满二叉树:
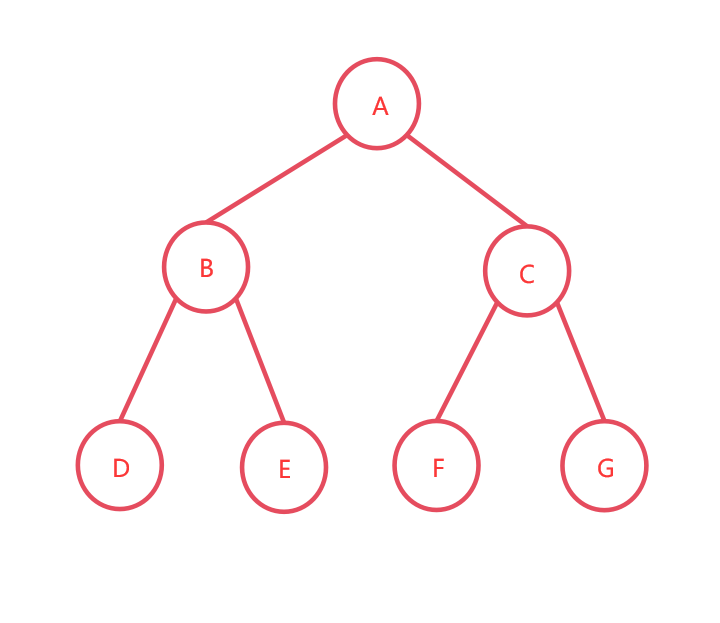
通过广义表表示该二叉树:
(A , ( B , ( D , E ) ) , ( C , ( F , G ) ) ) )
这个二叉树的解释如下:
根结点是A,它的左孩子是B,B的左孩子是D,B的右孩子是E。
根结点A的右孩子是C,C的左孩子是F,C的右孩子是G。