已知两个链表A和B分别表示两个集合,其元素递增排列。
请设计算法求出A与B的交集,并存放于A链表中。
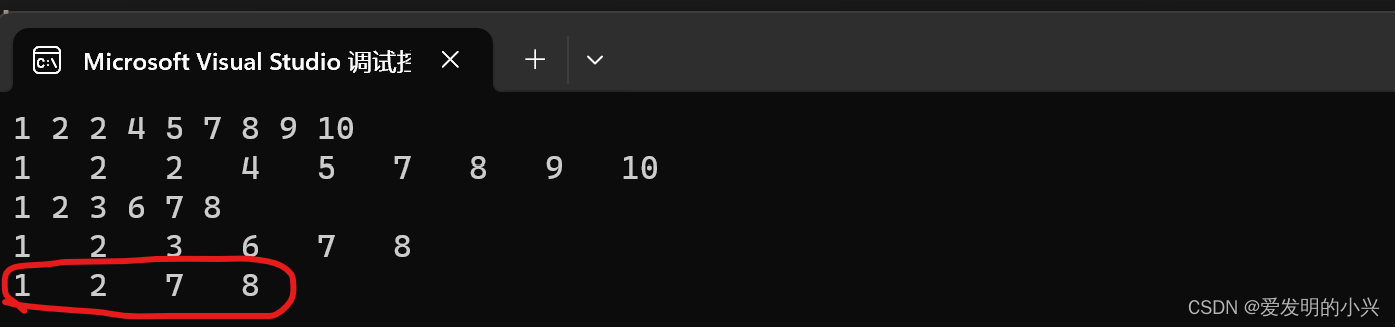
a: 1, 2, 2, 4, 5, 7, 8, 9, 10
b: 1, 2, 3, 6, 7, 8
#include <iostream>
using namespace std;typedef int Elemtype;
#define ERROR 0;
#define OK 1;typedef struct LNode
{Elemtype data; //结点保存的数据struct LNode* next; //结构体指针
}LNode, * LinkList;/*单链表初始化*/
bool Init_LinkList(LinkList& L)
{L = (LinkList)malloc(sizeof(LNode)); //新建头结点if (L == NULL){return ERROR;}L->data = 0;L->next = NULL;return OK;
}/*单链表头插法*/
bool LinkList_head_instert(LinkList& L)
{int x = 0;LNode* p = NULL;while (cin >> x){p = (LinkList)malloc(sizeof(LNode));if (p != NULL) //防止分配地址失败{p->data = x;p->next = L->next;L->next = p;if (cin.get() == '\n') break; //检测换行符}else{exit(0);cout << "内存分配失败" << endl;}}return OK;
}/*单链表尾插法*/
bool LinkList_tail_instert(LinkList& L)
{int x = 0;LNode* p = NULL;LNode* r = NULL;r = L;while (cin >> x){p = (LinkList)malloc(sizeof(LNode));if (p != NULL) //防止分配地址失败{p->data = x;p->next = NULL;r->next = p;r = p;if (cin.get() == '\n') break; //检测换行符}else{exit(0);cout << "内存分配失败" << endl;}}return OK;
}/*单链表遍历*/
bool LinkList_All_value(LinkList L)
{if (L->next == NULL){cout << "链表为空" << endl;return ERROR;}LNode* s = NULL;s = L->next;while (s != NULL){cout << s->data << " ";s = s->next;}cout << endl;free(s);return OK;
}/*单链表长度*/
int LinkList_length(LinkList L)
{int count = 0;LNode* s = NULL;s = L->next;while (s != NULL){count++;s = s->next;}return count;
}/*清空单链表*/
void Clear_LinkList(LinkList& L)
{LNode* p = L->next;LNode* q = NULL;while (p != NULL){q = p->next;free(p);p = q;}L->next = NULL;
}/*销毁单链表*/
void Destory_LinkList(LinkList& L)
{LNode* p = NULL;LNode* q = NULL;p = L;while (p != NULL){q = p->next;free(p);p = q;}L = NULL;
}bool jiaoji(LinkList& La, LinkList& Lb)
{LNode* pa = NULL;LNode* pb = NULL;LNode* pc = NULL;LNode* q = NULL;pa = La->next;pb = Lb->next;pc = La;La->next = NULL;if (pa == NULL && pb == NULL){cout << "两个单链表为空!!!" << endl;return ERROR;}while (pa != NULL && pb != NULL){if (pa->data == pb->data){pc->next = pa;pc = pa;pa = pa->next;q = pb;pb = pb->next;delete q;//或者用free(q);}else if (pa->data > pb->data){q = pb;pb = pb->next;delete q;}else //pa->data < pb->data{q = pa;pa = pa->next;delete q;}}while (pa != NULL){q = pa;pa = pa->next;delete q;}while (pb != NULL){q = pb;pb = pb->next;delete q;}pc->next = NULL;delete Lb;return OK;
}/*已知两个链表A和B分别表示两个集合,其元素递增排列。
请设计算法求出A与B的交集,并存放于A链表中。*/
//a: 1, 2, 2, 4, 5, 7, 8, 9, 10
//b: 1, 2, 3, 6, 7, 8int main(void)
{LinkList a = NULL;Init_LinkList(a);LinkList_tail_instert(a);//1 2 2 4 5 7 8 9 10LinkList_All_value(a);LinkList b = NULL;Init_LinkList(b);LinkList_tail_instert(b);//1 2 3 6 7 8LinkList_All_value(b);jiaoji(a, b);LinkList_All_value(a);//打印两个单链表的交集return 0;
}