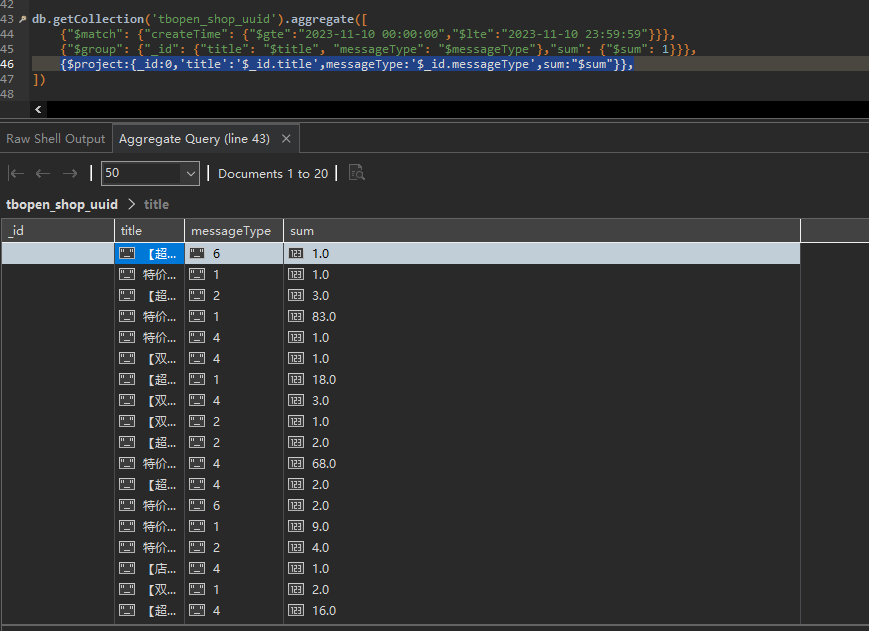
本文针对6大问题,从多角度分析了我国新能源电动汽车发展形势与前景。文中针对不同问题,采用了层次分析法、时间序列模型、机理模型、回归模型等数学方法。并结合实例数据,对相关模型进行求解,以量化预测了新能源电动汽车在政策驱动、市场竞争、温室气体减排等多个方面的潜在贡献。

对于影响因素识别问题,构建了层次分析模型。该模型通过构建判断矩阵,计算各层次间相对重要性,明确新能源汽车发展的决定性因素在政策支持上。模型计算简便,结果直观。对于新能源汽车销量预测问题,采用ARIMA联合多元回归方法。ARIMA模型合理预测解释变量未来趋势,回归模型建立变量之间关系。该方法预测效果良好。对于市场竞争问题,构建了拟合已有数据的机理模型。该模型反映了新能源汽车与传统车企之间复杂的市场竞争与份额变迁。模型形式简洁,结果符合实际规律。在分析政策干预问题上,引入多元线性回归。回归模型考虑政策变化对新能源汽车销量的潜在影响,对关键风险进行评估。对于环境效果问题,建立动力学模型,模拟电动车推广下的未来碳排路径。

（中间摘要略）在预测电动汽车环境效益问题上,建立了模拟渗透过程的动力学模型。模型合理地设置初始条件,以推广和人口数量为自变量,预测不同渗透率下的未来碳排放量。模型结果直观反映电动化比重提高对城市碳减排的促进作用。

最后,文章还对各类模型的优缺点与应用范围进行了归纳总结。为相关研究的模型选择与拓展提供了一定参考。

关键词：电动汽车、层次分析法、ARIMA时间序列预测、多元线性回归、机理模型、碳排放

视频讲解如下：

https://www.bilibili.com/video/BV1hj41177kb

一、摘要1

二、问题重述4

三、问题分析5

3.1 问题1分析5

3.2 问题2分析5

3.3 问题3分析5

3.4 问题4分析5

3.5 问题5分析5

3.6 问题6分析6

四、模型假设6

五、符号说明7

六、模型的建立和求解8

6.1 问题1电动汽车发展AHP影响模型的建立和求解8

6.1.1 影响因素一二级指标建立8

6.1.2 层次分析法AHP模型建立9

6.1.3 层次分析法AHP模型求解11

6.2 问题2电动汽车ARIMA与多元线性回归模型的建立和求解12

6.2.1 关键指标选取12

6.2.2 指标数据收集13

6.2.3 电动汽车销售量多元线性回归模型拟合17

6.2.4 影响汽车销售量的指标因素ARIMA预测20

6.2.5 电动汽车销售量多元线性回归预测24

6.3 问题3新能源与传统能源汽车竞争模型的建立和求解25

6.3.1 新能源与传统能源汽车竞争关系影响因素分析25

6.3.2 竞争关系的机理模型建立26

6.3.3 竞争关系机理模型数据收集26

6.3.4 竞争关系机理模型建立28

6.3.5 竞争关系机理模型的求解29

6.4 问题4政策对电动汽车的发展影响模型的建立和求解33

6.4.1 政策关键指标确定34

6.4.2 政府支持度数据收集34

6.4.3 多元线性回归拟合模型35

6.5 问题5电动汽车对碳排放影响模型的建立和求解36

6.5.1 碳中和时间预测因素37

6.5.2 预测模型的建立37

6.5.3 碳排放数据收集37

6.5.4 预测模型的求解39

6.6 问题6的公开信41

七、模型的评价42

7.1 问题1:AHP模型的评价42

7.2 问题2:回归与ARIMA模型的评价42

7.3 问题3:竞争关系机理模型的评价42

7.4 问题4:回归模型的评价43

7.5 问题5:动力学模型的评价43

问题重述

2023亚太杯数学建模竞赛C题问题重述如下：新能源汽车是指采用先进的技术原理、新技术和新结构，以非常规车用燃料为动力来源(非常规车用燃料是指除汽油和柴油以外的燃料)，并集成了车辆动力控制和驱动方面的先进技术的车辆。新能源汽车包括四大类:混合动力电动汽车、纯电动汽车、燃料电池电动汽车和其他新能源汽车。新能源电动汽车作为新能源汽车的一种，由于其低污染、低能耗、调峰能力强等特点，近年来获得了快速发展。新能源电动汽车，包括电动公交车和7座以下家用电动汽车，一直受到世界各国消费者和政府的欢迎。

自2011年以来，中国政府积极推动新能源电动汽车的发展，并制定了一系列优惠政策。新能源电动汽车产业取得巨大发展，逐渐成为继“中国高铁”之后的又一个中国标志。现在邀请您的团队完成以下问题:

问题1:分析影响我国新能源电动汽车发展的主要因素，建立数学模型，描述这些因素对我国新能源电动汽车发展的影响。

问题2:收集中国新能源电动汽车的行业发展数据，建立数学模型描述和预测未来10年中国新能源电动汽车的发展。

问题3:收集数据，建立数学模型，分析新能源电动汽车对全球传统能源汽车行业的影响。

问题4:一些国家制定了一系列有针对性的政策来抵制我国新能源电动汽车的发展。建立数学模型，分析这些政策对我国新能源电动汽车发展的影响。

问题5:分析城市新能源电动汽车(包括电动公交车)电动化对生态环境的影响。假设有100万城市人口，提供模型的计算结果。

问题6:根据问题5的结论，写一封致市民的公开信，宣传新能源电动汽车的好处以及世界各国电动汽车产业的贡献。

问题分析

问题1分析

2023亚太杯数学建模竞赛C题问题1分析如下：问题1是一个多准则决策问题。影响新能源电动汽车发展的因素较多,之间存在层次结构,比如准则层和指标层等。使用层次分析法(AHP)可以明确各层次因素的权重,找出对目标影响最大的关键因素,以此分析和描述这些因素对新能源电动汽车发展的影响。

问题2分析

2023亚太杯数学建模竞赛C题问题2分析如下：问题2是一个典型的时间序列预测问题。为了预测新能源电动汽车的未来发展,我们需要识别出影响发展的关键指标,包括政策支持度、经济增长等在内的多因素。这些指标自身也具有时间序列特征。可以使用ARIMA等模型预测这些关键因标的未来走势,然后结合多元线性回归来预测新能源电动汽车销量这一关键指标,实现对整个行业发展趋势的预测。

问题3分析

2023亚太杯数学建模竞赛C题问题3分析如下：问题3是一个市场竞争关系问题。新能源电动汽车作为新兴力量,对传统燃油车形成了挑战和替代,双方呈现竞争关系。可以建立竞争机理模型,考虑市场容量、产品替代性、消费者偏好等影响因素,模拟双方的市场份额变化趋势,分析新能源电动汽车发展对传统燃油车行业的冲击。

问题4分析

2023亚太杯数学建模竞赛C题问题4分析如下：问题4也可以视为一个多元回归问题。一些国家的针对性政策会对我国新能源电动汽车形成负面影响,我们需要量化这种影响的大小。可以选择政策相关的指标作为自变量,新能源电动汽车销量作为因变量,建立多元线性回归模型,分析政策变化对关键指标的影响,评估政策变化可能带来的风险。

问题5分析

2023亚太杯数学建模竞赛C题问题5分析如下：这是一个典型的碳排放预测问题。推广新能源电动汽车可以减少城市的碳排放。我们可以建立动力学模型,考虑人口增长、电动化比重提升、电网清洁化等多个因素,对城市碳排放量进行预测。并可以推算出不同情景下实现碳中和的时间,以定量分析新能源电动汽车的环境效益。

问题6分析

问题6是一个宣传类文章写作任务，需要结合问题5的分析结果,从城市碳中和的正面效益角度,向公众宣传新能源电动汽车的环境友好性。可以增加类比其他国家电动汽车发展的成功案例,使文章更有说服力。

模型假设

本文中5个问题使用的模型假设如下：

问题1假设

问题2假设

问题3假设

问题4假设

问题5假设

模型的建立和求解

问题1电动汽车发展AHP影响模型的建立和求解

问题1:分析影响我国新能源电动汽车发展的主要因素，建立数学模型，描述这些因素对我国新能源电动汽车发展的影响。

影响因素一二级指标建立

政策支持因素 (P)：

考虑政府的优惠政策，包括购车补贴、免税政策等。

定义政策支持因素 P，其值越大表示政府支持力度越大。

经济因素 (E)：

GDP增长率和人均收入水平对新能源电动汽车需求的影响。

定义经济因素 E，其值越大表示经济条件越有利。

技术创新因素 (T)：

考虑新技术的研发和应用，包括电池技术、充电技术等。

定义技术创新因素T，其值越大表示技术水平越先进。

层次分析法AHP模型建立

层次分析法（Analytic Hierarchy Process，AHP）是一种用于多因素决策的数学模型，适用于对不同因素之间的相对重要性进行比较和权重分配。我们可以使用AHP来分析影响我国新能源电动汽车发展的主要因素

以下是AHP的步骤：

步骤1：确定层次结构

建立层次结构，将问题分解为层次结构，包括目标、准则和子准则。在这里，我们可以将问题分为三个层次：目标（新能源电动汽车的发展）、准则（政策、经济、技术、基础设施、环境）、子准则（具体的政策、经济条件、技术水平、基础设施完善度、环境意识）。

步骤2：建立判断矩阵

对每个相邻层次的因素进行两两比较，使用1-9的尺度来表示相对重要性，其中1表示相等，3表示略有重要，9表示非常重要。构建判断矩阵。

步骤3：计算权重

通过对判断矩阵进行特征值分解，得到特征向量，归一化后得到权重向量。

步骤4：一致性检验

计算一致性比率，确保判断矩阵的一致性。如果一致性比率超过某个阈值，需要重新考虑比较矩阵。

步骤5：综合权重

将得到的各层次的权重综合，得到最终的权重。

步骤6：评估

利用所得的权重进行综合评估，确定各因素对新能源电动汽车发展的相对影响程度。

AHP模型涉及几个关键的步骤，包括构建比较矩阵、计算权重、一致性检验等。以下是AHP模型各个步骤的详细公式（略）

% 计算权重
[V, D] = eig(P_matrix);
max_eigenvalue = max(max(D));
index_max_eigenvalue = find(D == max_eigenvalue);
weights = V(:, index_max_eigenvalue) / sum(V(:, index_max_eigenvalue));% 一致性指标的计算
n = length(weights);
CI = (max_eigenvalue - n) / (n - 1);
RI = [0, 0, 0.58, 0.9, 1.12];  % 随机一致性指标，可根据矩阵大小调整
CR = CI / RI(n);disp('比较矩阵：');
disp(P_matrix);
disp('特征向量：');
disp(V);
disp('最大特征值：');
disp(max_eigenvalue);
disp('权重：');
disp(weights);
disp('一致性指标 CI：');
disp(CI);
disp('一致性比例 CR：');
disp(CR);% 如果 CR 大于某个阈值，可能需要重新调整比较矩阵以提高一致性

问题2电动汽车ARIMA与多元线性回归模型的建立和求解

问题2:收集中国新能源电动汽车的行业发展数据，建立数学模型描述和预测未来10年中国新能源电动汽车的发展。

关键指标选取

指标选取：

销售量（ V）：

表示新能源电动汽车的年销售量，是一个关键的指标。

政府支持度（P）：

衡量政府对新能源电动汽车的政策支持，包括补贴、减税等。

经济增长（ E）：

考虑国家经济的整体增长对汽车市场的影响。

技术创新（ T）：

考虑电池技术、充电技术等方面的创新对新能源汽车市场的推动。

基础设施建设（ I）：

衡量充电基础设施的建设程度，包括充电站的数量和分布。

指标数据收集

历史数据：收集过去几年的新能源电动汽车销售量、政府支持度、经济增长、技术创新和基础设施建设的数据。

这里，政府支持度使用补贴金额（亿元）、经济增长使用GDP增长率、技术创新使用每年发表的专利数量、基础设施建设使用充电站数量。

电动汽车销售量多元线性回归模型拟合

为了建立新能源电动汽车发展与给定指标之间的数学模型，可以使用多元线性回归模型。假设我们有五个指标（政府支持度，经济增长，技术创新，基础设施建设）作为自变量，而新能源电动汽车的销售量作为因变量。

影响汽车销售量的指标因素ARIMA预测

为了利用前面建立的多元线性回归模型，我们需要使用ARIMA模型预测影响汽车销售量的指标因素，

ARIMA（AutoRegressive Integrated Moving Average）模型是一种时间序列分析的方法，用于预测未来的值。它结合了自回归（AR）和移动平均（MA）的概念，同时考虑了时间序列的差分（Integrated）。ARIMA自相关和偏相关检测如下：

Mdl = arima(AR_Order, 0, MA_Order);  EstMdl = estimate(Mdl,data);[res,~,logL] = infer(EstMdl,data);   %res即残差stdr = res/sqrt(EstMdl.Variance);figure('Name','残差检验','Position',[317,151.4,985.0,450.4])
%     subplot(1,3,1)
%     plot(stdr)
%     title('Standardized Residuals')
%     subplot(1,3,2)
%     histogram(stdr,10)
%     title('Standardized Residuals')subplot(1,3,1)autocorr(stdr)subplot(1,3,2)parcorr(stdr)subplot(1,3,3)qqplot(stdr)exportgraphics(gcf,['img/',savename,'arima预测残差检验.png'],'Resolution',600)[forData,YMSE] = forecast(EstMdl,step,'Y0',data);   %matlab2018及以下版本写为Predict_Y(i+1) = forecast(EstMdl,1,'Y0',Y(1:i)); lower = forData - 1.96*sqrt(YMSE); %95置信区间下限upper = forData + 1.96*sqrt(YMSE); %95置信区间上限figure('Position',[489,343,811.2,303.6]);plot(data,'Color',[.7,.7,.7]);hold onh1 = plot(length(data):length(data)+step,[data(end);lower],'r:','LineWidth',2);plot(length(data):length(data)+step,[data(end);upper],'r:','LineWidth',2)h2 = plot(length(data):length(data)+step,[data(end);forData],'k','LineWidth',2);legend([h1 h2],'95% 置信区间','预测值',...'Location','NorthWest')exportgraphics(gcf,['img/',savename,'arima预测图.png'],'Resolution',600)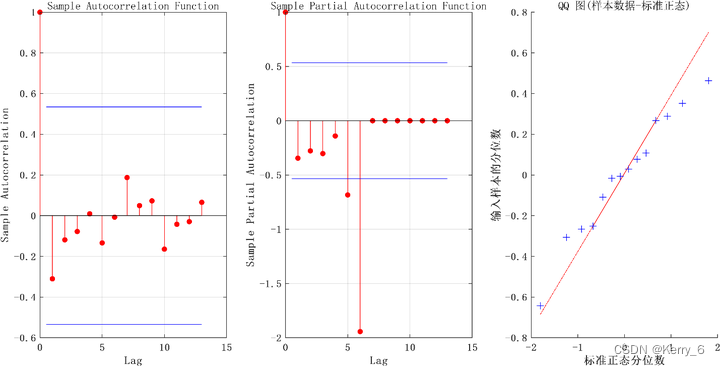

电动汽车销售量多元线性回归预测

电动汽车销售量多元线性回归预测结果如下：

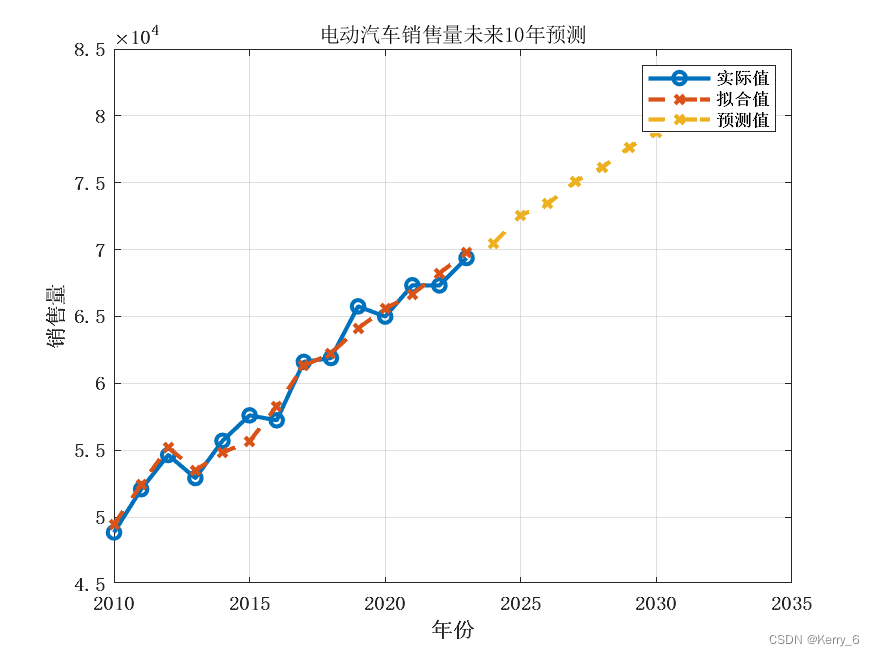
电动汽车销售量多元线性回归预测

问题3新能源与传统能源汽车竞争模型的建立和求解

问题3:收集数据，建立数学模型，分析新能源电动汽车对全球传统能源汽车行业的影响。

分析：新能源汽车行业的快速发展，给传统燃油汽车带来了极大的挑战，分析新能源电动汽车对全球传统能源汽车行业的影响，即研究我国新能源汽车与传统燃油汽车的市场竞争关系，分析该竞争关系受到哪些因素的影响，给出我国新能源汽车和传统燃油汽车市场保有量随时间变化的演化规律。

新能源与传统能源汽车竞争关系影响因素分析

中国新能源汽车与传统燃油汽车的市场竞争关系受到多种因素的影响，包括政策支持、技术进步、消费者需求、燃油价格等。下面将就这些因素对市场竞争关系的影响进行分析。

政策支持：

中国政府出台了大量的支持新能源汽车发展的政策，这些政策包括减免购置税、车船税、免收高速公路通行费等，对于新能源汽车的市场推广和普及起到了积极的推动作用。同时，政府也在一定程度上限制传统燃油汽车的生产和销售，从而使得新能源汽车在市场上的竞争优势更加明显。

技术进步：

随着科技的不断进步，新能源汽车的性能和续航能力得到了显著提升，消费者对其认知和接受程度也逐渐提高。相比之下，传统燃油汽车已经达到了技术的瓶颈，无法再有太大的突破，因此在市场上的竞争力逐渐下降。

消费者需求：

在环保和能源节约等方面，消费者对新能源汽车的需求越来越高。同时，年轻一代消费者的观念也日益注重环保、可持续发展等方面，这些因素都使得新能源汽车在市场上的竞争力逐渐增强。

燃油价格：

燃油价格的波动会直接影响到传统燃油汽车的销售和使用。当燃油价格较低时，消费者更愿意购买传统燃油汽车；而当燃油价格较高时，消费者更倾向于购买新能源汽车。

竞争关系的机理模型建立

基于以上因素，中国新能源汽车与传统燃油汽车的市场竞争关系呈现出以下演化规律：

随着政府对新能源汽车政策支持的不断加大，新能源汽车的销量逐渐上升，而传统燃油汽车的销量则逐渐下降。（略）

竞争关系机理模型建立

基于上述因素，可以采用以下数学模型来描述中国新能源汽车和传统燃油汽车市场保有量随时间变化的演化规律：（略）

其中，N t表示新能源汽车的保有量（单位：万辆），Ne表示传统燃油汽车的保有量（单位：万辆），P f表示燃油价格（单位：元/升），t表示时间（单位：年）。k1、k2和k3为系数，a和b为常数，t0表示初始时间。这个模型包括两个部分：新能源汽车的保有量和传统燃油汽车的保有量。对于新能源汽车的保有量，我们假设它与燃油价格之间存在某种函数关系，这里采用了一个S形函数；而对于传统燃油汽车的保有量，我们假设它是指数增长的。

​