完全背包
有N件物品和一个最多能背重量为W的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品都有无限个(也就是可以放入背包多次),求解将哪些物品装入背包里物品价值总和最大。
题目链接:
题目页面
求解思路:
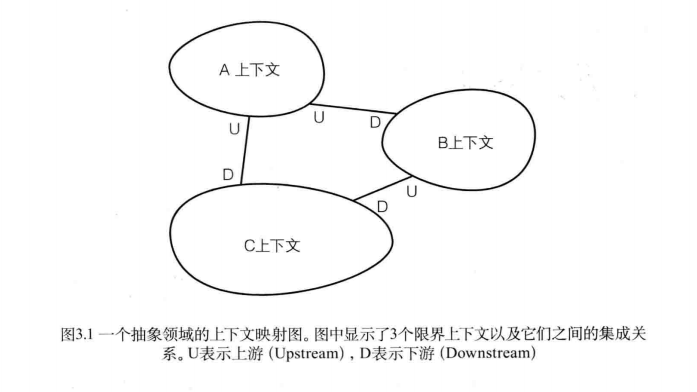
完全背包和01背包的唯一不同就是在遍历顺序上;完全背包先遍历背包或是物品都可以,并且需要正序遍历
代码:
#include <iostream>
#include <vector>
using namespace std;void solve(vector<int> weight, vector<int> value, int bagWeight){vector<int> dp(bagWeight+1, 0);for (int i = 0; i < weight.size(); i++){for (int j = 0; j <= bagWeight; j++){if (j - weight[i] >= 0)dp[j] = max(dp[j], dp[j-weight[i]] + value[i]);}}cout << dp[bagWeight] << endl;
}int main(){int N, V;cin >> N >> V;vector<int> weight;vector<int> value;for (int i = 0; i < N; i++){int w, v;cin >> w >> v;weight.push_back(w);value.push_back(v);}solve(weight, value, V);return 0;
}518. 零钱兑换 II
题目链接:
力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台
求解思路:
本题是要求凑成总金额的物品组合个数
动规五部曲
- 确定dp数组及其下标含义:凑成总金额j的货币组合数为dp[j]
- 递推公式:dp[j] += dp[j - coins[i]];(01背包题目 494.目标和)
- dp数组的初始化:dp[0] = 1
- 确定遍历顺序:本题应该先遍历物品,再遍历背包(求组合数)
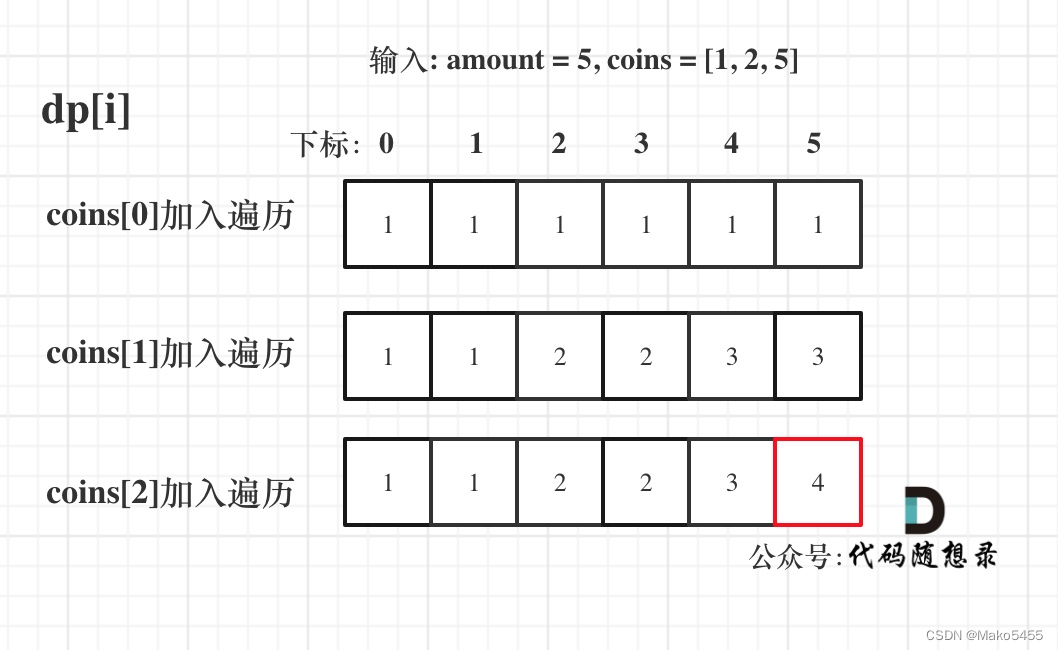
- 举例推导dp数组:amount = 5, coins = [1, 2, 5] ,dp状态图如下
代码:
class Solution {
public:int change(int amount, vector<int>& coins) {vector<int> dp(amount + 1);dp[0] = 1;// 先物品再背包,求组合数for (int i = 0; i < coins.size(); i++){for (int j = coins[i]; j <= amount; j++){dp[j] += dp[j-coins[i]];}}return dp[amount];}
};377. 组合总和 Ⅳ
题目链接:
力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台
求解思路:
和上一题仅仅是遍历顺序不一样
代码:
class Solution {
public:int combinationSum4(vector<int>& nums, int target) {vector<int> dp(target+1, 0);dp[0] = 1;// 先遍历背包,再遍历物品(求排列)for (int i = 0; i <= target; i++){for (int j = 0; j < nums.size(); j++){// C++测试用例有两个数相加超过int的数据// 需要在if里加上dp[i] < INT_MAX - dp[i - num]if (i - nums[j] >= 0 && dp[i] < INT_MAX - dp[i - nums[j]])dp[i] += dp[i - nums[j]];}}return dp[target];}
};