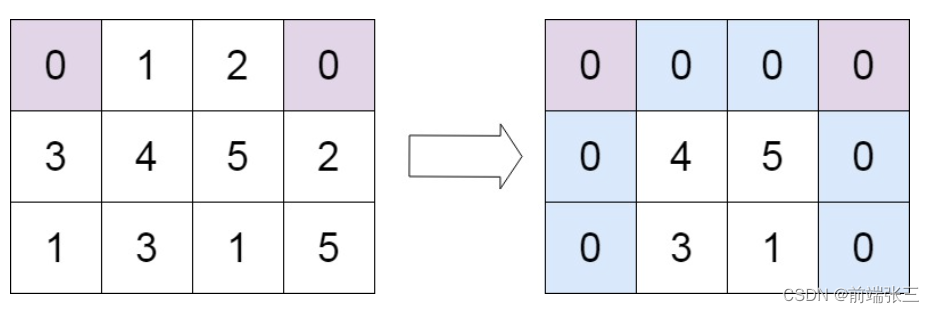
本文的代码与数据地址已上传至github:https://github.com/helloWorldchn/MachineLearning
一、FCM算法简介
1、模糊集理论
L.A.Zadeh在1965年最早提出模糊集理论,在该理论中,针对传统的硬聚类算法其隶属度值非0即1的严格隶属关系,使用模糊集合理论,将原隶属度扩展为 0 到 1 之间的任意值,一个样本可以以不同的隶属度属于不同的簇集,从而极大提高了聚类算法对现实数据集的处理能力,由此模糊聚类出现在人们的视野。FCM算法广泛应用在数据挖掘、机器学习和计算机视觉与图像处理等方向。
2、FCM算法
模糊C均值聚类(Fuzzy C-means)算法简称FCM算法,是软聚类方法的一种。FCM算法最早由Dunn在1974年提出然后经 Bezdek推广。
硬聚类算法在分类时有一个硬性标准,根据该标准进行划分,分类结果非此即彼。
软聚类算法更看重隶属度,隶属度在[0,1]之间,每个对象都有属于每个类的隶属度,并且所有隶属度之和为 1,即更接近于哪一方,隶属度越高,其相似度越高。
3、算法思想
模糊 C-均值聚类(FCM)算法一种软聚类的聚类方法,该方法的思想使用
隶属度来表示每个数据之间的关系,从而确定每个数据点属于的聚类簇的聚类方法。同时 FCM 算法也是一种基于目标函数的算法,给定含有n个数据的数据集: X = { x 1 , x 2 , … x i , … , x n } X=\left\{\right.x_1,x_2,…x_i,…,x_n\left\}\right. X={x1,x2,…xi,…,xn}, X i X_i Xi是第 i i i个特征向量; X i j X_{ij} Xij是 X i Xi Xi的第 j j j个属性。每个样本包含 d d d个属性。FCM算法可以将该数据集划分为 K K K类, K K K为大于1的正整数,其中 K K K个类的聚类中心分别为 [ v 1 , v 2 , … , v n ] [v_1,v _2,…,v_n] [v1,v2,…,vn]。
FCM的目标函数和约束条件如下:
J ( U , V ) = ∑ i = 1 n ∑ j = 1 k u i j m d i j 2 J(U,V)=\displaystyle\sum_{i=1}^{n} \displaystyle\sum_{j=1}^{k} u_{ij}^md_{ij}^2 J(U,V)=i=1∑nj=1∑kuijmdij2
∑ j = 1 k u i j = 1 , u i j ∈ [ 0 , 1 ] \displaystyle\sum_{j=1}^{k} u_{ij}=1, u_{ij}∈[0,1] j=1∑kuij=1,uij∈[0,1]
其中, u i j u_{ij} uij是样本点 x i x_i xi与聚类中心 v j v_j vj的隶属度,m是模糊指数(m>1), d i j d_{ij} dij是样本点 x i x_i xi与聚类中心 v j v_j vj的距离,一般采用欧氏距离。聚类即是求目标函数在约束条件的最小值。FCM 算法通过对目标函数的迭代优化来取得对样本集的模糊分类。
为使目标函数 J 取得最小值,在满足约束条件的情况下对目标函数使用拉格朗日(Lagrange)乘数法,得到隶属度矩阵U和聚类中心 v j v_j vj。
u i j = 1 ∑ c = 1 k ( d i j d i k ) 2 m − 1 u_{ij}=\frac{1}{\displaystyle\sum_{c=1}^{k} (\frac{d_{ij}}{d_{ik}}) ^\frac{2}{m-1}} uij=c=1∑k(dikdij)m−121
v j = ∑ i = 1 n u i j m x i ∑ i = 1 n u i j m v_j=\frac{\displaystyle\sum_{i=1}^{n} u_{ij}^m x_i }{\displaystyle\sum_{i=1}^{n} u_{ij}^m } vj=i=1∑nuijmi=1∑nuijmxi
4、算法步骤
算法的具体描述如下:
输入:聚类数K,初始聚类中心 X = { x 1 , x 2 , … x i , … , x n } X=\left\{\right.x_1,x_2,…x_i,…,x_n\left\}\right. X={x1,x2,…xi,…,xn},模糊指标m,终止误差
输出:聚类中心 [ v 1 , v 2 , … , v k ] [v_1,v _2,…,v_k] [v1,v2,…,vk],隶属度矩阵 u i j u_{ij} uij
Step1:初始化参数值k、m和迭代允许的误差ε;
Step2:初始化迭代次数l=0和隶属度矩阵U(0) ;
Step3:根据上一步的公式分别计算或更新隶属度矩阵和新的聚类中心。
Step4:比较 J l J^l Jl和 J ( l − 1 ) J^{(l-1)} J(l−1) ;若 ∣ ∣ J l − J ( l − 1 ) ∣ ∣ ≤ ε || J^{l} - J^{(l-1)} || ≤ ε ∣∣Jl−J(l−1)∣∣≤ε,则满足迭代停止条件,迭代停止。否则置 l = l + 1 l=l+1 l=l+1,返回Step3,继续迭代。
伪代码如下:
输入:数据集合X, 聚类的类别数k ,迭代次数阈值 T ,迭代次数 t ;
输出:聚类中心V, 隶属度矩阵U u = 进行初始化;init U; //隶属度矩阵U初始化calculate v ;//根据公式计算聚类中心点calculate u ;//根据公式计算隶属度更新并组成隶属度矩阵Ucalculate J; //计算目标函数 J ;t += 1; if t > Treturn Celse返回步骤 2;end if
FCM流程图如下:

二、代码实现(Python3)
本文使用的数据集为UCI数据集,分别使用鸢尾花数据集Iris、葡萄酒数据集Wine、小麦种子数据集seeds进行测试,本文从UCI官网上将这三个数据集下载下来,并放入和python文件同一个文件夹内即可。同时由于程序需要,将数据集的列的位置做出了略微改动。数据集具体信息如下表:
| 数据集 | 样本数 | 属性维度 | 类别个数 |
|---|---|---|---|
| Iris | 150 | 4 | 3 |
| Wine | 178 | 3 | 3 |
| Seeds | 210 | 7 | 3 |
数据集在我主页资源里有,免积分下载,如果无法下载,可以私信我。
1、Python3代码实现
from pylab import *
import pandas as pd
import numpy as np
import operator
import math
import matplotlib.pyplot as plt
import random
from sklearn.decomposition import PCA
from sklearn.preprocessing import LabelEncoder
from sklearn.metrics import normalized_mutual_info_score # NMI
from sklearn.metrics import rand_score # RI
from sklearn.metrics import accuracy_score # ACC
from sklearn.metrics import f1_score # F-measure# 数据保存在.csv文件中
iris = pd.read_csv("dataset/iris.csv", header=0) # 鸢尾花数据集 Iris class=3
wine = pd.read_csv("dataset/wine.csv") # 葡萄酒数据集 Wine class=3
seeds = pd.read_csv("dataset/seeds.csv") # 小麦种子数据集 seeds class=3
wdbc = pd.read_csv("dataset/wdbc.csv") # 威斯康星州乳腺癌数据集 Breast Cancer Wisconsin (Diagnostic) class=2
glass = pd.read_csv("dataset/glass.csv") # 玻璃辨识数据集 Glass Identification class=6
df = iris # 设置要读取的数据集
# print(df)
columns = list(df.columns) # 获取数据集的第一行,第一行通常为特征名,所以先取出
features = columns[:len(columns) - 1] # 数据集的特征名(去除了最后一列,因为最后一列存放的是标签,不是数据)
dataset = df[features] # 预处理之后的数据,去除掉了第一行的数据(因为其为特征名,如果数据第一行不是特征名,可跳过这一步)
class_labels = list(df[columns[-1]]) # 原始标签
attributes = len(df.columns) - 1 # 属性数量(数据集维度)
k = 3 # 聚类簇数
MAX_ITER = 20 # 最大迭代数
n = len(dataset) # 样本数
m = 2.00 # 模糊参数# 初始化模糊矩阵U
def initializeMembershipMatrix():membership_mat = list()for i in range(n):random_num_list = [random.random() for i in range(k)]summation = sum(random_num_list)temp_list = [x / summation for x in random_num_list] # 首先归一化membership_mat.append(temp_list)return membership_mat# 计算类中心点
def calculateClusterCenter(membership_mat):cluster_mem_val = zip(*membership_mat)cluster_centers = list()cluster_mem_val_list = list(cluster_mem_val)for j in range(k):x = cluster_mem_val_list[j]x_raised = [e ** m for e in x]denominator = sum(x_raised)temp_num = list()for i in range(n):data_point = list(dataset.iloc[i])prod = [x_raised[i] * val for val in data_point]temp_num.append(prod)numerator = map(sum, zip(*temp_num))center = [z / denominator for z in numerator] # 每一维都要计算。cluster_centers.append(center)return cluster_centers# 更新隶属度
def updateMembershipValue(membership_mat, cluster_centers):# p = float(2/(m-1))data = []for i in range(n):x = list(dataset.iloc[i]) # 取出文件中的每一行数据data.append(x)distances = [np.linalg.norm(list(map(operator.sub, x, cluster_centers[j]))) for j in range(k)]for j in range(k):den = sum([math.pow(float(distances[j] / distances[c]), 2) for c in range(k)])membership_mat[i][j] = float(1 / den)return membership_mat, data# 得到聚类结果
def getClusters(membership_mat):cluster_labels = list()for i in range(n):max_val, idx = max((val, idx) for (idx, val) in enumerate(membership_mat[i]))cluster_labels.append(idx)return cluster_labelsdef fuzzyCMeansClustering():# 主程序membership_mat = initializeMembershipMatrix()curr = 0start = time.time() # 开始时间,计时while curr <= MAX_ITER: # 最大迭代次数cluster_centers = calculateClusterCenter(membership_mat)membership_mat, data = updateMembershipValue(membership_mat, cluster_centers)cluster_labels = getClusters(membership_mat)curr += 1print("用时:{0}".format(time.time() - start))# print(membership_mat)return cluster_labels, cluster_centers, data, membership_matlabels, centers, data, membership = fuzzyCMeansClustering()def clustering_indicators(labels_true, labels_pred):if type(labels_true[0]) != int:labels_true = LabelEncoder().fit_transform(df[columns[len(columns) - 1]]) # 如果标签为文本类型,把文本标签转换为数字标签f_measure = f1_score(labels_true, labels_pred, average='macro') # F值accuracy = accuracy_score(labels_true, labels_pred) # ACCnormalized_mutual_information = normalized_mutual_info_score(labels_true, labels_pred) # NMIrand_index = rand_score(labels_true, labels_pred) # RIreturn f_measure, accuracy, normalized_mutual_information, rand_indexF_measure, ACC, NMI, RI = clustering_indicators(class_labels, labels)
print("F_measure:", F_measure, "ACC:", ACC, "NMI", NMI, "RI", RI)
# print(centers)
center_array = array(centers)
label = array(labels)
datas = array(data)
if attributes > 2:dataset = PCA(n_components=2).fit_transform(dataset) # 如果属性数量大于2,降维
# 做散点图
plt.scatter(dataset[:, 0], dataset[:, 1], marker='o', c='black', s=7) # 原图
plt.show()
colors = np.array(["red", "blue", "green", "orange", "purple", "cyan", "magenta", "beige", "hotpink", "#88c999"])
# 循换打印k个簇,每个簇使用不同的颜色
for i in range(k):plt.scatter(dataset[nonzero(label == i), 0], dataset[nonzero(label == i), 1], c=colors[i], s=7)
# plt.scatter(center_array[:, 0], center_array[:, 1], marker='x', color='m', s=30) # 聚类中心
plt.show()
2、聚类结果分析
本文选择了F值(F-measure,FM)、准确率(Accuracy,ACC)、标准互信息(Normalized Mutual Information,NMI)和兰德指数(Rand Index,RI)作为评估指标,其值域为[0,1],取值越大说明聚类结果越符合预期。
F值结合了精度(Precision)与召回率(Recall)两种指标,它的值为精度与召回率的调和平均,其计算公式见公式:
P r e c i s i o n = T P T P + F P Precision=\frac{TP}{TP+FP} Precision=TP+FPTP
R e c a l l = T P T P + F N Recall=\frac{TP}{TP+FN} Recall=TP+FNTP
F − m e a s u r e = 2 R e c a l l × P r e c i s i o n R e c a l l + P r e c i s i o n F-measure=\frac{2Recall \times Precision}{Recall+Precision} F−measure=Recall+Precision2Recall×Precision
ACC是被正确分类的样本数与数据集总样本数的比值,计算公式如下:
A C C = T P + T N T P + T N + F P + F N ACC=\frac{TP+TN}{TP+TN+FP+FN} ACC=TP+TN+FP+FNTP+TN
其中,TP(True Positive)表示将正类预测为正类数的样本个数,TN (True Negative)表示将负类预测为负类数的样本个数,FP(False Positive)表示将负类预测为正类数误报的样本个数,FN(False Negative)表示将正类预测为负类数的样本个数。
NMI用于量化聚类结果和已知类别标签的匹配程度,相比于ACC,NMI的值不会受到族类标签排列的影响。计算公式如下:
N M I = I ( U , V ) H ( U ) H ( V ) NMI=\frac{I\left(U,V\right)}{\sqrt{H\left(U\right)H\left(V\right)}} NMI=H(U)H(V)I(U,V)
其中H(U)代表正确分类的熵,H(V)分别代表通过算法得到的结果的熵。
其具体实现代吗如下:
由于数据集中给定的正确标签可能为文本类型而不是数字标签,所以在计算前先判断数据集的标签是否为数字类型,如果不是,则转化为数字类型
def clustering_indicators(labels_true, labels_pred):if type(labels_true[0]) != int:labels_true = LabelEncoder().fit_transform(df[columns[len(columns) - 1]]) # 如果标签为文本类型,把文本标签转换为数字标签f_measure = f1_score(labels_true, labels_pred, average='macro') # F值accuracy = accuracy_score(labels_true, labels_pred) # ACCnormalized_mutual_information = normalized_mutual_info_score(labels_true, labels_pred) # NMIrand_index = rand_score(labels_true, labels_pred) # RIreturn f_measure, accuracy, normalized_mutual_information, rand_indexF_measure, ACC, NMI, RI = clustering_indicators(labels_number, labels)
print("F_measure:", F_measure, "ACC:", ACC, "NMI", NMI, "RI", RI)
如果需要计算出聚类分析指标,只要将以上代码插入实现代码中即可。
3、聚类结果
- 鸢尾花数据集Iris


- 葡萄酒数据集Wine

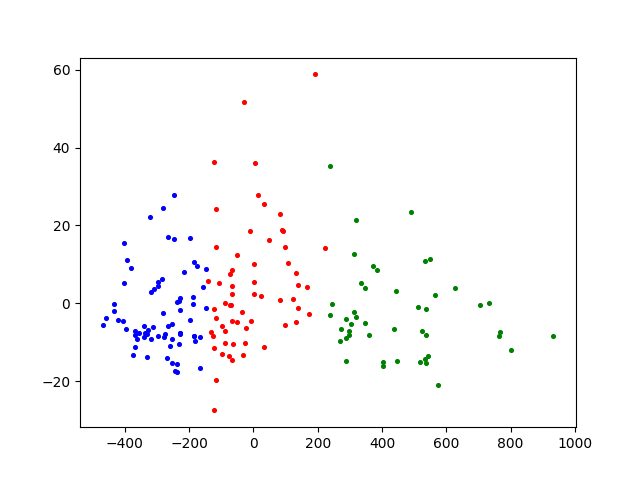
- 小麦种子数据集Seeds


4、FCM算法的不足
FCM算法的核心步骤就是通过不断地迭代,更新聚类簇中心,达到簇内距离最小。算法的时间复杂度很低,因此该算法得到了广泛应用,但是该算法存在着许多不足,主要不足如下:
- FCM聚类的簇数目需要用户指定。FCM算法首先需要用户指定簇的数目K值,K值的确定直接影响聚类的结果,通常情况下,K值需要用户依据自己的经验和对数据集的理解指定,因此指定的数值未必理想,聚类的结果也就无从保证。
- FCM算法的初始中心点选取上采用的是随机的方法。FCM算法极为依赖初始中心点的选取:一旦错误地选取了初始中心点,对于后续的聚类过程影响极大,很可能得不到最理想的聚类结果,同时聚类迭代的次数也可能会增加。而随机选取的初始中心点具有很大的不确定性,也直接影响着聚类的效果。
- FCM采用欧氏距离进行相似性度量,在非凸形数据集中难以达到良好的聚类效果。