题目1:343 整数拆分
题目链接:整数拆分
对题目的理解
将正整数n,拆分成k个正整数的和(k>=2)使得这些整数的乘积最大化,返回最大乘积
动规五部曲
1)dp数组的含义以及其下标i的含义
dp[i]:对 i 进行拆分,得到最大的乘积为dp[i]
2)递推公式
dp[i] = j*(i-j) 将i拆分成2个数j和-j
dp[i] = j*dp[i-j] 将i拆分成3个或3个以上的数
因为要求的是最大乘积,所以递推公式为dp[i]=max(j*(i-j),j*dp[i-j],dp[i])
3)dp数组初始化
dp[0] = 0 0只能拆成0+0,而题目要求至少拆分成两个正整数的和,所以初始化dp[0]没有意义
dp[1] = 0 1只能拆成0+1,而题目要求至少拆分成两个正整数的和,所以初始化dp[1]没有意义
dp[2] = 1 只能拆分成1+1,是两个正整数
所以只初始化dp[2]就ok
4)遍历顺序
dp[i]根据dp[i-j],所以i一定是从前向后遍历,且i是从3开始遍历,j是从1开始遍历(因为i-j>=2)
5)打印dp数组
代码
class Solution {
public:int integerBreak(int n) {//定义dp数组int dp[n+1];//初始化dp数组dp[2]=1;//递推for(int i=3;i<=n;i++){for(int j=1;j<i;j++){dp[i]=max(max(j*(i-j),j*dp[i-j]),dp[i]);}}return dp[n];}
};这段代码会报错

报错的原因是因为dp数组使用int直接定义,不会内部初始化为0,而是任意值,所以造成这种超时错误,所以需要使用vector进行数组的定义,使用vector会默认将数组的元素定义为0
将代码改正,使用vector定义
class Solution {
public:int integerBreak(int n) {//定义dp数组vector<int> dp(n+1);//初始化dp数组dp[2]=1;//递推for(int i=3;i<=n;i++){for(int j=1;j<i;j++){dp[i]=max(max(j*(i-j),j*dp[i-j]),dp[i]);}}return dp[n];}
};- 时间复杂度:O(n^2)
- 空间复杂度:O(n)
题目2:96 不同的二叉搜索树
题目链接:不同的二叉搜索树
对题目的理解
由n个节点组成,节点值从1到n互不相同的二叉搜索树有多少种
首先明确二叉搜索树长什么样
二叉搜索树是一个有序树:
- 若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
- 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
- 它的左、右子树也分别为二叉搜索树
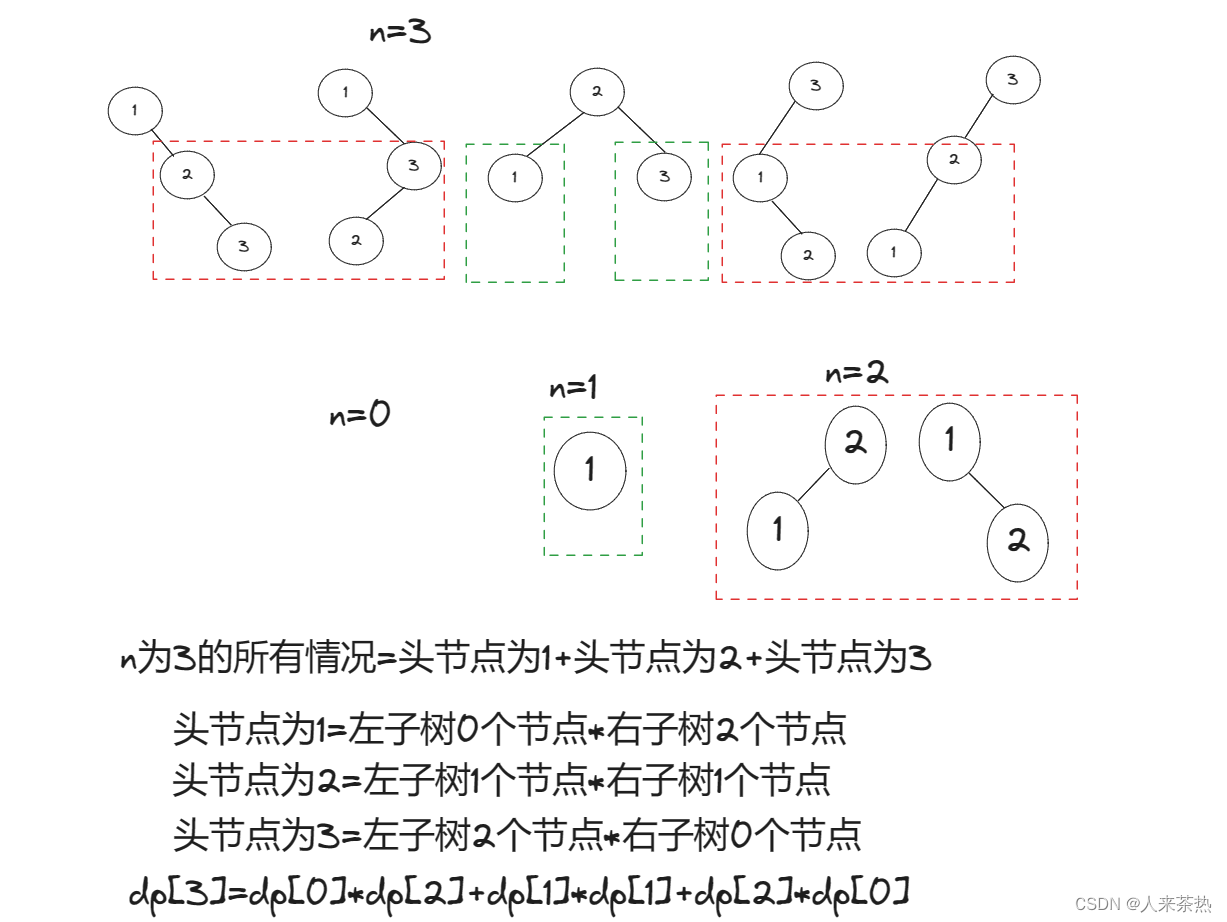
从图中可以看出,n为3时,当根节点为1和3时,它的左右子树布局与n为2时相同,只是数值不同而已,当根节点为2时,它的左右子树的布局与n为1时相同,因此找到了内部推导关系
动规五部曲
1)dp数组的含义以及下标i的含义
dp[i]:节点值从1到i的二叉搜索树的种类
2)递推公式
以j为头节点(j会枚举头节点从1到i),那么以j为头节点的左子树就是j-1,右子树就是i-j
dp[i] += dp[j-1] * dp[i-j],dp[i]收录节点i的所有情况(节点值从1到i二叉树的种类)
3)dp数组初始化
dp[0]=1,空子树也是一种二叉搜索树
4)遍历顺序
根据递推公式,dp[i] += dp[j-1] * dp[i-j],节点i的二叉搜索树种类,都是依靠其之前的节点确定的,所以节点要从小到大遍历
5)打印dp数组
代码
class Solution {
public:int numTrees(int n) {//定义dp数组vector<int> dp(n+1);//初始化dp数组dp[0] = 1;//递推for(int i=1;i<=n;i++){//因为节点值从1到n,每一个值都要作为根节点,都是一类情况for(int j=1;j<=i;j++){//j枚举所有从1到i所有头节点的情况dp[i]+=dp[j-1]*dp[i-j];//左子树是j-1个节点,右子树是i-j个节点}}return dp[n];}
};- 时间复杂度:O(n^2)
- 空间复杂度:O(n)