算法的奥秘:种类、特性及应用详解(算法导论笔记1)
上期总结算法的种类和大致介绍,这一期主要讲常见的六种算法详解以及演示。
排序算法:
排序算法是一类用于对一组数据元素进行排序的算法。根据不同的排序方式和时间复杂度,有多种排序算法。常见的排序算法包括冒泡排序、选择排序、插入排序、快速排序、归并排序等。
冒泡排序:通过不断比较相邻元素并交换顺序,使得较大的元素逐渐“浮”到数组的末尾,如同气泡一样。
选择排序:每次从未排序的元素中选择最小(或最大)的元素,放到已排序的末尾。
插入排序:将未排序的元素一个个插入到已排序的数组中,从而逐步形成排序好的数组。
快速排序:通过选择一个基准元素将数组分成两部分,一部分小于基准元素,一部分大于基准元素,然后递归地对这两部分继续进行快速排序。
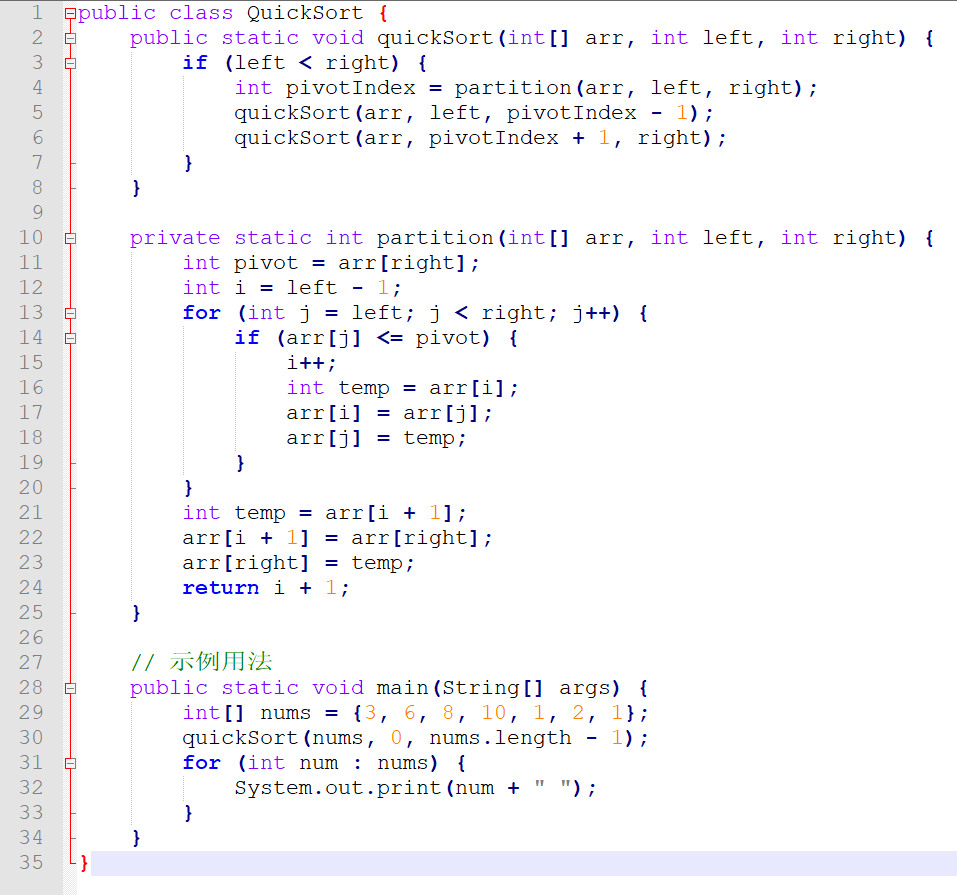
快速排序算法的实现包括两个主要部分:quickSort和partition。quickSort方法用于递归地排序子数组,而partition方法则用于将数组分为两个子数组,并返回基准元素的索引。在partition方法中,我们选择数组的最后一个元素作为基准,然后将小于等于基准的元素移到左边,大于基准的元素移到右边。最后,我们返回基准元素的索引,以便在quickSort方法中进一步分割子数组。在示例用法中,我们创建了一个包含七个整数的数组,并对其进行快速排序。
归并排序:采用分治策略,将数组分成若干个子数组,分别进行排序,最后将排好序的子数组合并成完整的排好序的数组。
查找算法:
查找算法用于在数据结构中查找特定元素。常见的查找算法包括线性查找和二分查找等。
线性查找:从数据结构的一端开始逐个比较每个元素,直到找到目标元素或遍历完整个数据结构。
二分查找:在有序的数据结构中,通过不断缩小查找范围来进行查找。首先确定查找范围的最左端和最右端,然后根据目标元素与中间元素的比较结果来确定下一步查找的方向,不断缩小查找范围直至找到目标元素或确定目标元素不存在为止。
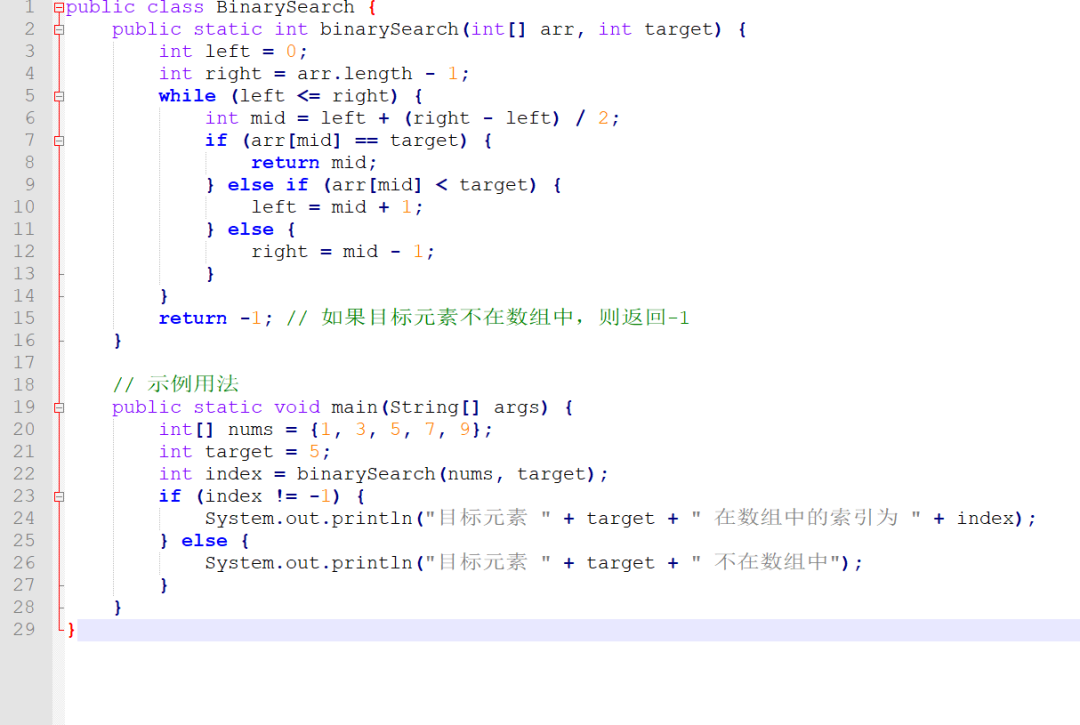
二分查找算法是一种高效的查找算法,它要求待查找的数组必须是有序的。该算法的基本思想是将数组分成两个部分,然后根据目标元素与中间元素的比较结果,将查找范围缩小一半。具体来说,我们首先将查找范围设为整个数组,然后通过比较目标元素与中间元素的大小,不断将查找范围缩小,直到找到目标元素或确定目标元素不存在为止。在示例用法中,我们创建了一个包含五个整数的数组,并使用二分查找算法查找目标元素5的位置。如果目标元素存在,则输出其位置;否则输出“目标元素不存在”。
图论算法:
图论算法用于解决图论问题,如最短路径、最小生成树、网络流等。常见的图论算法包括Dijkstra算法、Prim算法、Kruskal算法等。
Dijkstra算法:用于求解单源最短路径问题,给定一个有向图和一个起点,求出从起点到图中所有其他节点的最短路径。
Prim算法:用于求解最小生成树问题,在一个无向加权图中找到一棵包含所有节点且权值和最小的树。
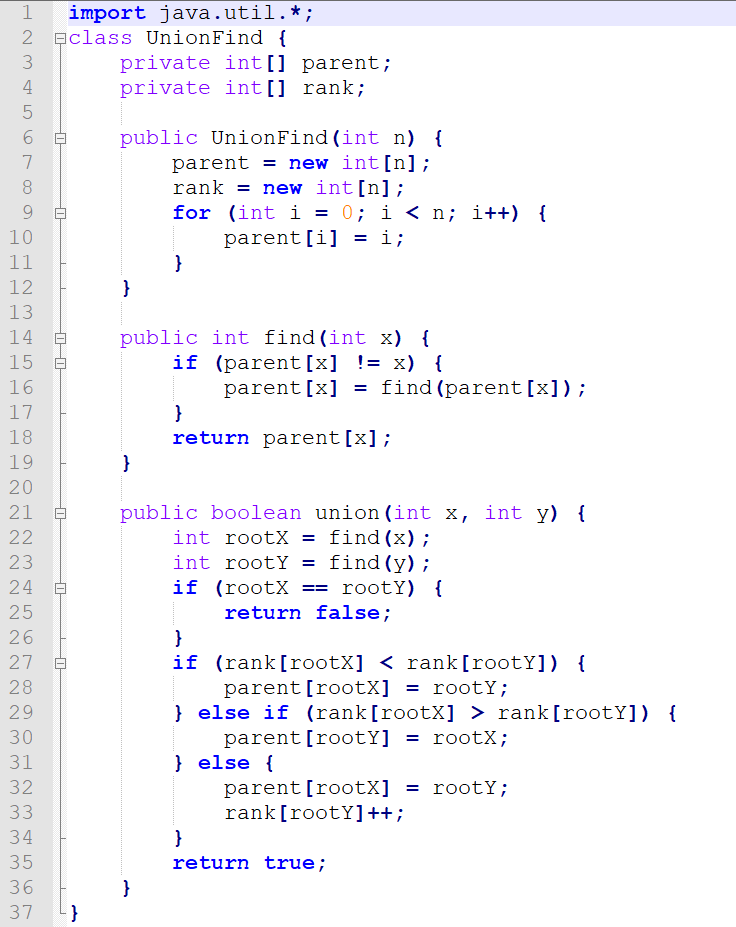
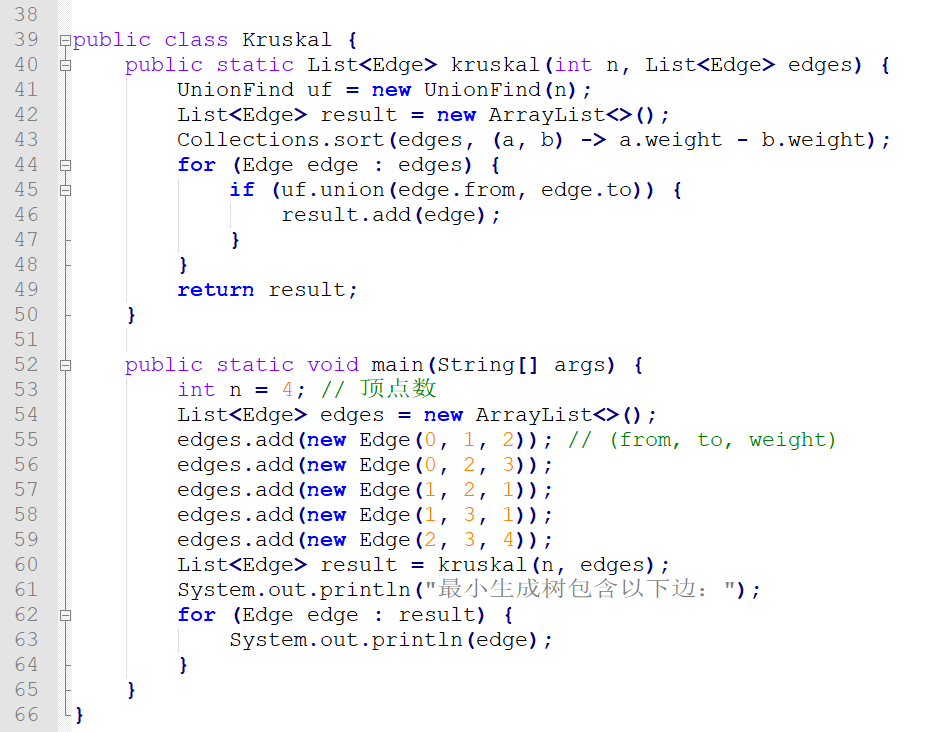
Kruskal算法:用于求解最小生成树问题,通过不断添加边来构建最小生成树,直至所有节点都被覆盖。
动态规划算法:
动态规划算法用于解决最优化问题,通过将问题分解为若干个子问题,并记录子问题的解,从而避免重复计算,提高求解效率。常见的动态规划算法包括背包问题、最大子段和问题等。
背包问题:给定一组物品,每种物品都有自己的重量和价值,背包的总容量有限。求解如何选择物品放入背包使得背包内的总价值最大。
最大子段和问题:给定一个整数数组,求解连续的子数组使得其和最大。
分治算法:
分治算法将问题分解为若干个子问题,分别解决这些子问题,然后将子问题的解合并以得到原问题的解。常见的分治算法包括快速排序、归并排序等。
快速排序:通过选择一个基准元素将数组分成两部分,一部分小于基准元素,一部分大于基准元素,然后递归地对这两部分继续进行快速排序。最后将排好序的子数组合并成完整的排好序的数组。
归并排序:采用分治策略,将数组分成若干个子数组
贪心算法:
贪心算法是一种解决问题的策略,它的思想是每一步都选择当前情况最好或最优(即最有利)的选择,希望通过这样的选择来得到全局最优解。这种算法在每一步中都只考虑当前情况下最好或最优的选择,而不会考虑这样的选择会对后续的结果产生什么样的影响。
举个例子来说,比如找零问题:假设我们需要在钱币面额为100元、50元、20元、10元、5元和1元的钱柜中找零,贪心算法会首先选择100元的钱币,然后是50元,以此类推,直到我们找到足够的零钱。这种策略虽然不一定能找到最优解(即使用最少数量的钱币),但通常能找到一个接近最优解的结果。
贪心算法的优点在于它每一步的操作都非常简单明了,也容易实现。同时,由于它每一步都选择最优解,所以它的时间复杂度通常比较低。但是,贪心算法并不适用于所有问题,有些问题使用贪心算法可能会得到局部最优解,但不一定能得到全局最优解。因此,当我们使用贪心算法时,需要先判断它是否适用于当前的问题。
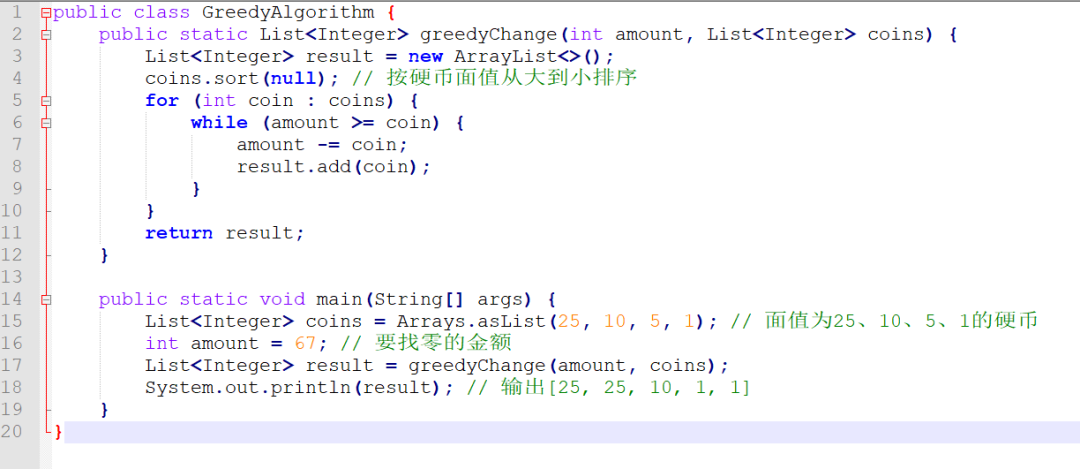
这个算法首先将硬币按照面值从大到小排序,然后从面值最大的硬币开始找零,尽可能多地使用这种硬币,直到找零的金额无法再使用这种硬币为止。然后,算法使用下一种面值较大的硬币,重复上述过程,直到找零的金额减到0为止。在实现中,我们将硬币按照面值从大到小排序,然后依次枚举每种硬币,计算使用这种硬币能够找零多少金额,然后将这种硬币加入结果列表中。重复这个过程,直到找零的金额减到0为止。