直线
题目描述
本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。
在平面直角坐标系中,两点可以确定一条直线。如果有多点在一条直线上, 那么这些点中任意两点确定的直线是同一条。
给定平面上 2 × 3 个整点(x,y)∣0≤x<2,0≤y<3,x∈Z,y∈Z,即横坐标 是 0到1 (包含 0 和 1) 之间的整数、纵坐标是 0 到 2 (包含 0 和 2) 之间的整数 的点。这些点一共确定了 11 条不同的直线。
给定平面上 20×21 个整点 (x,y)∣0≤x<20,0≤y<21,x∈Z,y∈Z,即横 坐标是 0 到 19 (包含 0 和 19) 之间的整数、纵坐标是 0 到 20 (包含 0 和 20) 之 间的整数的点。
请问这些点一共确定了多少条不同的直线。
解题思路
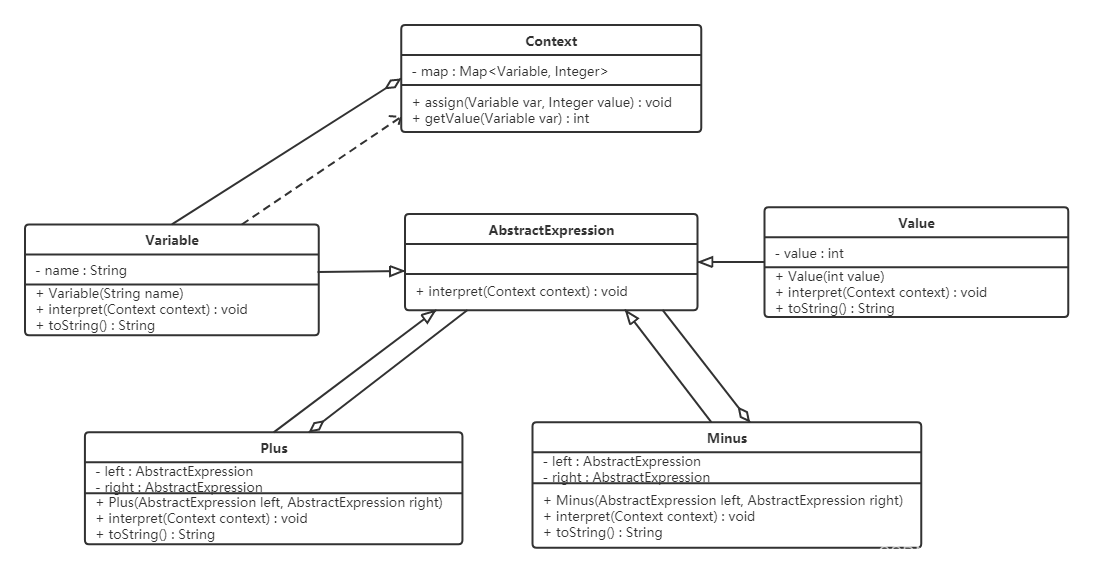
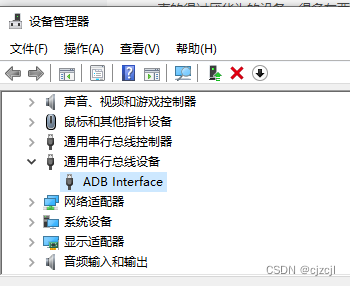
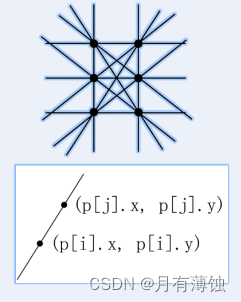
本题用点斜式:y=kx+b来表示直线。那么枚举所有点对构成的直线,判断k,b直线是新的,还是之前已经枚举过的,采用pair<double,double>存下k和b,如何判断当前直线是否为初次遇到的新直线呢?可用map判断是否是新的直线。对一条新的直线,映射(mao)成1,并统计累加,让ans++,下一次再找到这条直线,那么该直线的map值已经为1了,就不重复统计。分析题述中给定平面上2×3个整点,所确定的11条直线如下图:3条横向,2条竖线和6条斜线。
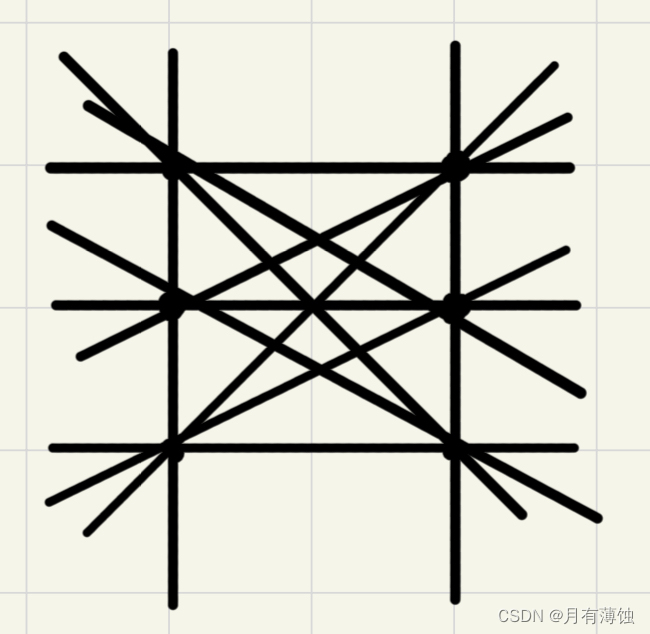
不妨首先把横线和竖线的条数统计到linenum直线总数中。根据题意,横坐标是0到19(包含0和19)之间的整数,那么竖线有20条,即col=20;纵坐标是0到20,那么有21条横线,即row=21。横线和竖线条数加起来先计入linenum,初值linunum=row+col。
然后来求斜线,由于任意两点可以确定一条直线。那么枚举所有的点,嵌套的两重循环i和j,都去枚举所有的点,点i和点j就能确定一条直线,现在来判断(i,j)构造出来的直线line(k,b)是否之前已经计入过linenum中。
如果是初次遇见的新直线line,那么就map其为1,并且计入linenum,即linenum++;否则表示之前已经出现过此直线line(k,b),就无需统计。一对(k,b)就能表示出一条直线。在枚举所有点之前,需要先保存所有点,存入数组p中。已知i、j两点,如何计算(k,b)?
用如下公式即可:
k=(p[j].y-p[i].y)/(p[j].x-p[i].x);
b=(p[j].xp[i].y-p[j].yp[i].x)/p[i].x-p[i].x);
最终答案:40257
C++代码
#include<iostream>
#include<map>
#include<utility>
using namespace std;struct point{double x,y;
}p[25*25];map<pair<double,double>,int>line;//pair存斜率 k 和截距 b
//map是STL的一个关联容器,他提供一对一的数据处理能力,使 点 与 直线 成 一对一对应关系
//用 (x,y) 这个点作为索引,并拥有相关联的指向 line(int)的指针
//pair是将2个数据组合成一组数据 。 x,y 这两个数据组合成一个点 (x,y)以及 将 k,b这两个数据合成一组数据 int main()
{//struct point p[25*25];int cnt=0;int col=20,row=21;int i,j;for(i=0;i<col;i++){for(j=0;j<row;j++){p[cnt].x=i;p[cnt++].y=j;}}int linenum=col+row;//先确定横线和竖线的数量 for(i=0;i<cnt;i++){for(j=0;j<cnt;j++){if(p[i].x==p[j].x||p[i].y==p[j].y)//跳过横线和竖线 continue;//k=(y2-y1)/(x2-x1)//b=(x1y2-x2y1)/(x1-x2)double k=(p[j].y-p[i].y)/(p[j].x-p[i].x);double b=(p[i].x*p[j].y-p[j].x*p[i].y)/(p[i].x-p[j].x);if(line[{k,b}]==0){line[{k,b}]=1;linenum++;}} }cout<<linenum<<endl;return 0;
}