凸性
凸性(convexity)在优化算法的设计中起到至关重要的作用, 这主要是由于在这种情况下对算法进行分析和测试要容易。 换言之,如果算法在凸性条件设定下的效果很差, 那通常我们很难在其他条件下看到好的结果。 此外,即使深度学习中的优化问题通常是非凸的, 它们也经常在局部极小值附近表现出一些凸性。 这可能会产生一些像 (Izmailov et al., 2018)这样比较有意思的新优化变体。
%matplotlib inline
import numpy as np
import torch
from mpl_toolkits import mplot3d
from d2l import torch as d2l定义
在进行凸分析之前,我们需要定义凸集(convex sets)和凸函数(convex functions)。
凸集
凸集(convex set)是凸性的基础。简单地说,如果对于任何连接a和b的线段也位于x中,则向量空间中的一个集合x是凸(convex)的。 在数学术语上,这意味着对于所有
。
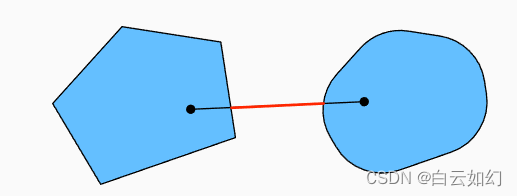
这听起来有点抽象,第一组存在不包含在集合内部的线段,所以该集合是非凸的,而另外两组则没有这样的问题。
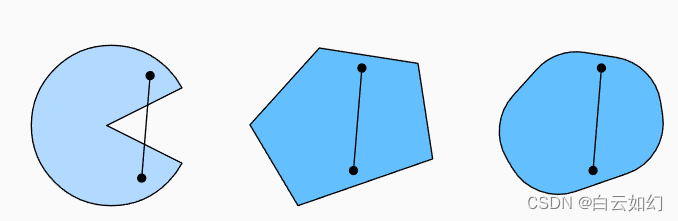
设X和Y是凸集,那么也是凸集的。 现在考虑任意
, 因为X和Y是凸集, 所以连接a和b的线段包含在
和
中。 鉴于此,它们也需要包含在
中,从而证明我们的定理。
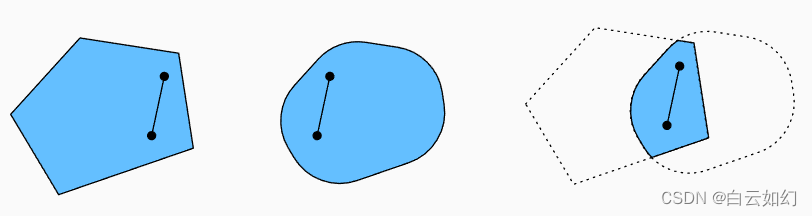
因此线段也不在中,因此证明了凸集的并集不一定是凸的,即非凸(nonconvex)的。
通常,深度学习中的问题是在凸集上定义的。在某些情况下,我们使用有界长度的变量,例如球的半径.