一、场景
有时候我们会遇到这样的场景,比如:M={1,4,6,8},N={2,4,5,7},我的需求就是判断{1,2}是否属于同一个集合,当然实现方法有很多,一般情况下,普通青年会做出 O(MN)的复杂度,那么有没有更轻量级的复杂度呢?并查集就是用来解决这个问题的。
二、操作
从名字可以出来,并查集其实只有两种操作,并(Union)和查(Find),并查集是一种算法,所以我们要给它选择一个好的数据结构,通常我们用树来作为它的底层实现。
2.1、节点定义
#region 树节点/// <summary>/// 树节点/// </summary>public class Node{/// <summary>/// 父节点/// </summary>public char parent;/// <summary>/// 节点的秩/// </summary>public int rank;}#endregion
2.2、Union 操作
<1> 原始方案
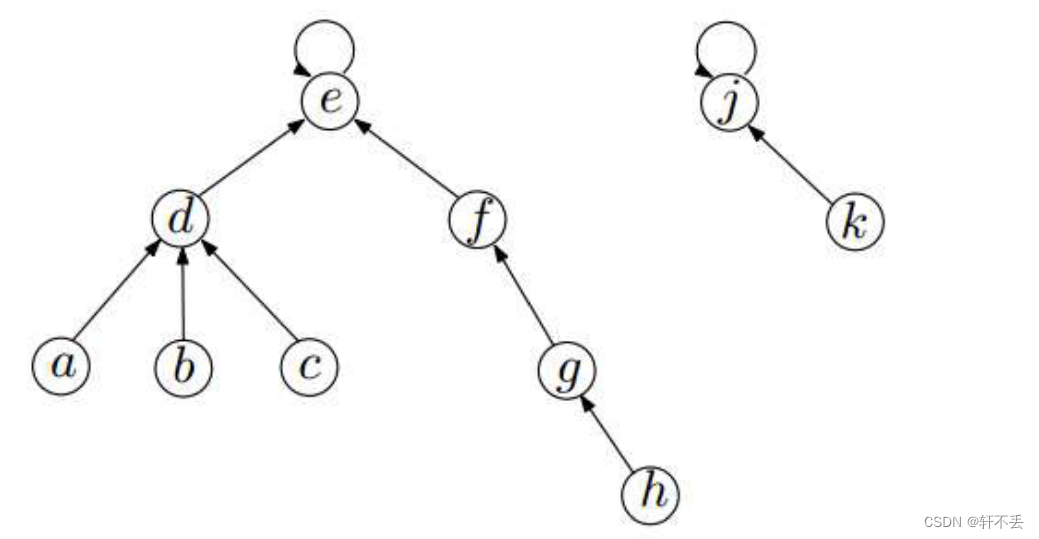
首先我们会对集合的所有元素进行打散,最后每个元素都是一个独根的树,然后我们 Union 其中某两个元素,让他们成为一个集合,最坏情况下我们进行 M 次的 Union 时会存在这样的一个链表的场景。
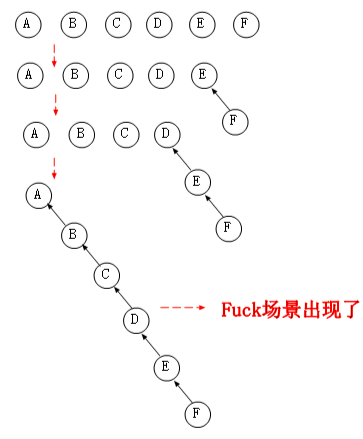
从图中我们可以看到,Union 时出现了最坏的情况,而且这种情况还是比较容易出现的,最终导致在 Find 的时候就相当复杂了,为 O(N)。
<2> 按秩合并
我们发现出现这种情况的原因在于我们 Union 时都是将合并后的大树作为小树的孩子节点存在,那么我们在 Union 时能不能判断一下,将小树作为大树的孩子节点存在,最终也就降低了新树的深度,比如图中的 Union(D,{E,F})的时候可以做出如下修改。
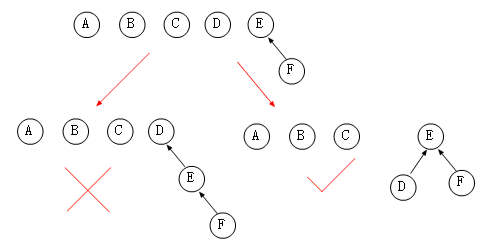
可以看出,我们有效的降低了树的深度,在 N 个元素的集合中,构建树的深度不会超过 LogN 层。M 次操作的复杂度为 O(MlogN),从代码上来说,我们用 Rank 来统计树的秩,可以理解为树的高度,独根树时 Rank=0,当两棵树的 Rank 相同时,可以随意挑选合并,在新根中的 Rank++ 就可以了。
#region 合并两个不相交集合/// <summary>/// 合并两个不相交集合/// </summary>/// <param name="root1"></param>/// <param name="root2"></param>/// <returns></returns>public void Union(char root1, char root2){char x1 = Find(root1);char y1 = Find(root2);//如果根节点相同则说明是同一个集合if (x1 == y1)return;//说明左集合的深度 < 右集合if (dic[x1].rank < dic[y1].rank){//将左集合指向右集合dic[x1].parent = y1;}else{//如果 秩 相等,则将 y1 并入到 x1 中,并将x1++if (dic[x1].rank == dic[y1].rank)dic[x1].rank++;dic[y1].parent = x1;}}#endregion
2.3、Find 操作
我们学算法,都希望能把一个问题优化到不能优化的地步,针对 logN 的级别,我们还能优化吗?当然可以。
<1> 路径压缩
在 Union 和 Find 这两种操作中,显然我们在 Union 上面已经做到了极致,下面我们在 Find 上面考虑一下,是不是可以在 Find 上运用伸展树的思想,这种伸展思想就是压缩路径。
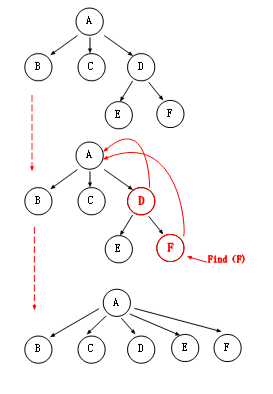
从图中我们可以看出,当我 Find(F)的时候,找到“F”后,我们开始一直回溯,在回溯的过程中给,把该节点的父亲指向根节点。最终我们会形成一个压缩后的树,当我们再次 Find(F)的时候,只要 O(1)的时间就可以获取,这里有个注意的地方就是 Rank,当我们在路径压缩时,最后树的高度可能会降低,可能你会意识到原先的 Rank 就需要修改了,所以我要说的就是,当路径压缩时,Rank 保存的就是树高度的上界,而不仅仅是明确的树高度,可以理解成"伸缩椅"伸时候的长度。
#region 查找x所属的集合/// <summary>/// 查找x所属的集合/// </summary>/// <param name="x"></param>/// <returns></returns>public char Find(char x){//如果相等,则说明已经到根节点了,返回根节点元素if (dic[x].parent == x)return x;//路径压缩(回溯的时候赋值,最终的值就是上面返回的"x",也就是一条路径上全部被修改了)return dic[x].parent = Find(dic[x].parent);}#endregion
我们注意到,在路径压缩后,我们将 LogN 的复杂度降低到 Alpha(N),Alpha(N)可以理解成一个比 hash 函数还有小的常量,这就是算法的魅力。