项杰
一、说明
不确定性校准是机器学习中最容易被误解的概念之一。它可以概括为这个简单的问题:“鉴于上述下雨的可能性,您是否带伞?”
我们在日常生活中使用主观概率和不确定性校准的概念,但没有意识到它们。对于不确定性校准良好的天气预报模型来说,如果下雨的概率只有 5%,那么带伞可能就不值得了。从频率论的角度来看,如果可以通过大量随机试验反复观察上图早上7点的天气情况,那么只有5%会下雨。然而,另一方面,如果不确定性校准不当,那么早上 7 点的随机试验中 40% 可能最终会下雨——这是一个很大的意外惊喜。
二、什么是不确定度校准?
德格鲁特等人以预报降雨为例说明校准的概念。
校准的概念涉及预报员的预测与实际观测到的相对降雨频率之间的一致性。粗略地说,如果预测者在预测为 x 的这些天中,长期相对频率也是 x,则可以说他是经过良好校准的。
换句话说,对于一个校准良好的模型,如果它预测一组图像中有 40% 的概率是猫,那么该组图像中包含猫的频率应该等于 40%。“相对频率”有时被称为“条件概率”,可以理解为以预测概率为 40% 为条件的 cat,即积极结果的概率。
Dawid [1] 提出了类似的过程,如下所示。
将预测与现实进行比较的一种方法是挑选一些相当任意的测试天集,并将 (a) 相关事件实际发生的天数比例 p 与 (b) 这些天的平均预测概率 π 进行比较。
如果我们遵循某种划分方案来选择比较(a)和(b)的测试集,我们就会得到可靠性图。
三、可靠性图
在二元分类问题中,我们训练一个模型来估计示例被分类为正类的概率,即 f(x_i)=p(y_i=1|x_i),如下图 1 所示。

图 1. 估计一组示例的概率
一旦我们获得了测试集的概率,我们就将概率划分为 K 个子集,其中每个子集代表 0 到 1 之间不相交的概率区间。如图 2 所示。
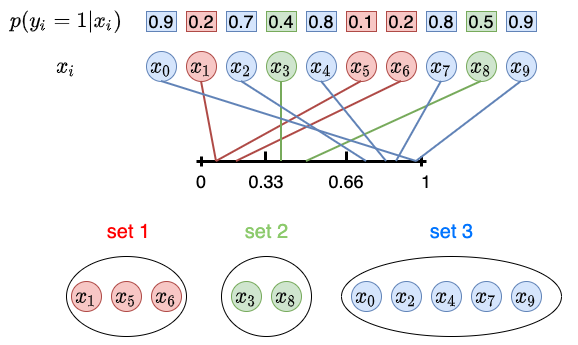
图 2。示例根据区间 [0, 0.33)、[0.33, 0.66) 和 [0.66, 1] 分为三组。
对于不同颜色的每个子集,我们计算两个估计:(a)平均预测概率,(b)正例的相对频率。
我们首先计算 (a) 每个子集的平均预测概率,如图 3 所示。
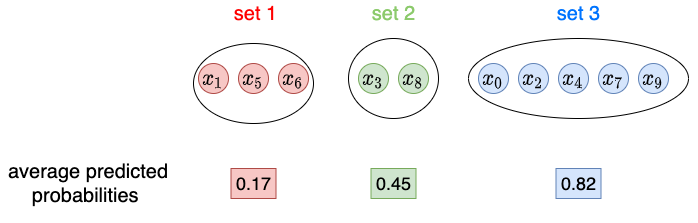
图 3. 每个子集的平均预测概率。
接下来我们计算(b)正例的相对频率,这需要了解真实标签的知识。在图4中,我们使用灰色圆圈表示负类,其余颜色表示正类。举个例子,在集合 1 中,只有一个例子是正例;因此,正例的相对频率为1/3。
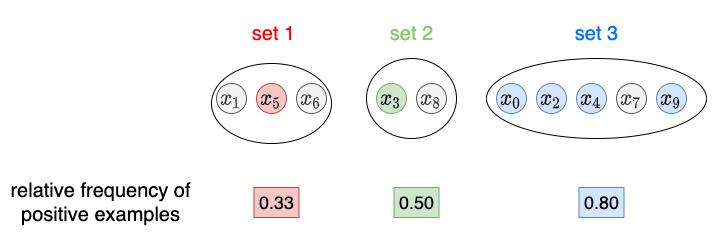
图 4. 正面例子的相对频率
可靠性图是根据 (a) 绘制 (b) 的图,如图 5 所示。
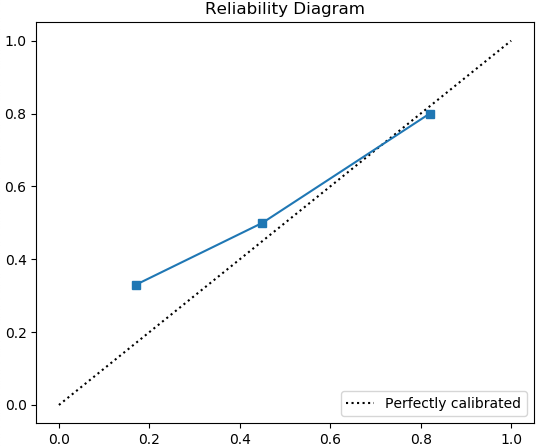
图 5. 可靠性图
直观地,校准图表明: (I) 当平均预测概率为 0.17 时,大约 33% 的预测是正的;(II) 当平均预测概率为 0.45 时,大约 50% 的预测为正;(III) 当平均预测概率为 0.82 时,大约 80% 的预测是肯定的。这个设计的模型虽然并不完美,但校准得相对较好。
四、误解:相对频率与准确度
关于可靠性图的一个普遍误解是用“准确度”代替“相对频率”。有时,从业者——包括我非常尊敬的著名研究人员——用“每个子集的准确性”来表示相对频率,这并不是校准的本意。我们需要从相对频率的角度来理解校准,其中正类的预测置信度应该反映所有预测中正例的频率(有时称为子集的流行度)而不是准确性。
我将使用scikit-learn [3]中的示例来展示它们之间的差异。图 6 显示了逻辑回归模型的可靠性图,该模型的校准相对较好。
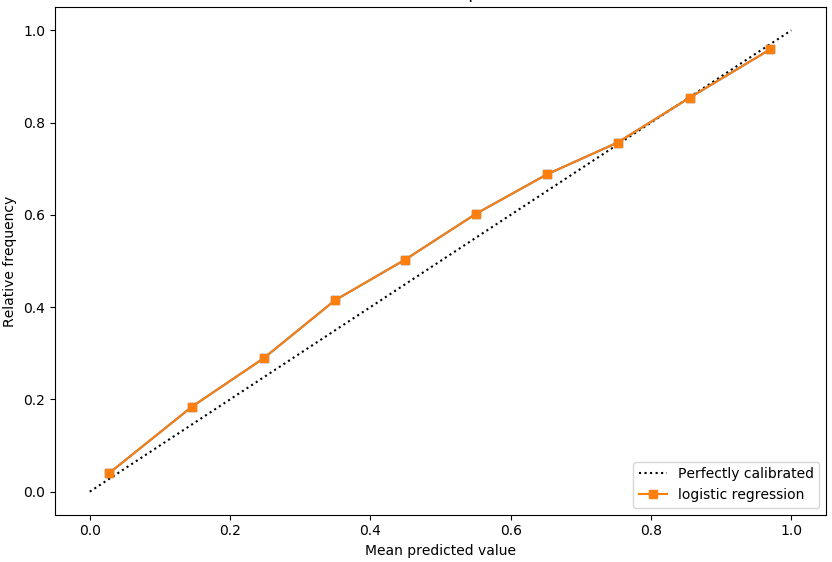
图 6. 可靠性图
但是,如果我使用精度绘制 y 轴,它看起来像 V 形曲线,如图 7 所示。
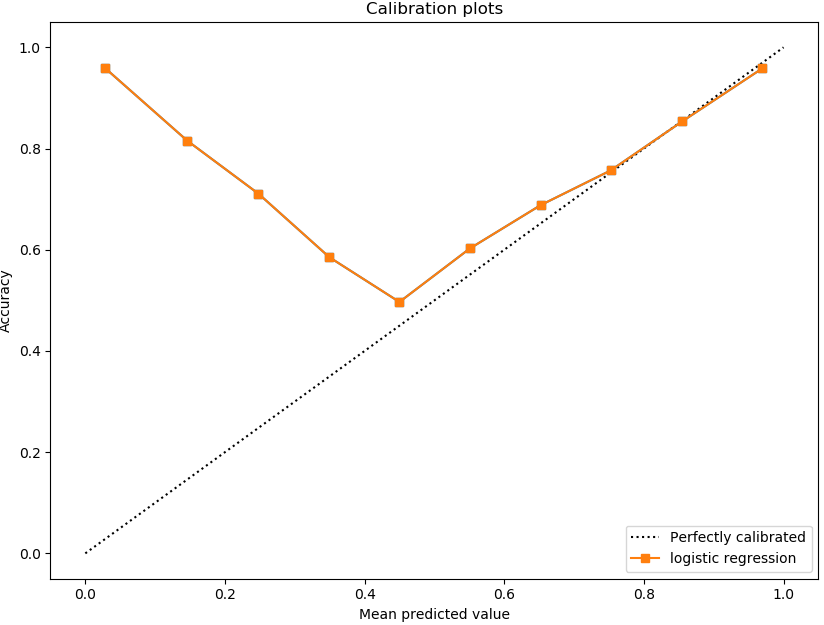
图 7. 准确度-平均预测值图
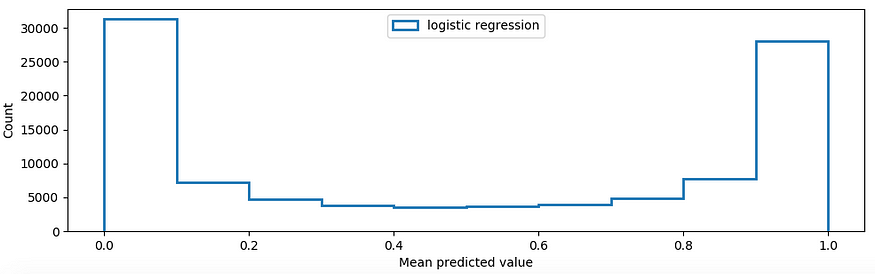
这是因为当阳性预测概率较低而阴性概率较高时,会抬高图的左半部分。这可以通过平均预测值的直方图来验证。大量示例的平均预测值在 0 到 0.1 之间,因为它们是负类,并且大多数示例都被模型正确分类。
五、结论
希望您永远不会担心天气预报的不确定性校准。如果当下雨的概率低于 20% 时你总是被淋湿,你就知道预测模型校准不当。
从机器学习从业者的角度来看,不确定性校准与模型概率结果的解释高度相关,特别是在医疗领域等安全关键应用中。
六、参考
[1] 德格鲁特、莫里斯 H. 和斯蒂芬 E. 费伯格。“预测者的比较和评估。” 《皇家统计学会杂志》:D 系列(统计学家) 32.1–2 (1983):12–22.APA
[2] Dawid, A. Philip. “The well-calibrated Bayesian.” Journal of the American Statistical Association 77.379 (1982): 605–610.APA
[3] sklearn.calibration.calibration_curve — scikit-learn 1.3.2 documentation