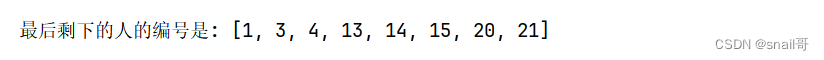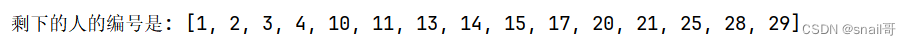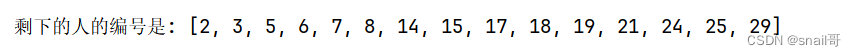每日一练：约瑟夫生者死者小游戏

在这里插入图片描述

1. 问题描述

约瑟夫问题（Josephus problem）是一个经典的数学和计算机科学问题，源于犹太历史学家弗拉维奥·约瑟夫斯（Flavius Josephus）的著作《犹太战记》。问题的描述如下：
在这个问题中，有n个人站成一个圈，从1到n编号。从第一个人开始，每次数m个人，数到第m个人就将其从圈中删除，然后从下一个人开始重新数，重复这个过程，直到所有人都被删除。问题是，最后剩下的那个人的编号是多少？
为了解决约瑟夫问题，可以使用递归或迭代的方法。下面是一个简单的递归解法的伪代码：

function josephus(n, m):if n == 1:return 1else:return (josephus(n - 1, m) + m - 1) % n + 1

这个递归函数的基本思想是：假设已知n-1个人的问题的解，那么在这个基础上，考虑第n个人加入的情况。在每一轮中，我们实际上将问题规模缩小为n-1个人。
注意，这里的编号是从1开始的，因为在问题的原始描述中，人的编号是从1到n的。在某些变体中，编号可能从0开始，因此在实现时需要注意这一点。

2. 解题思路

解决约瑟夫问题的一般思路是通过模拟每一轮的删除过程，不断更新当前位置，并在满足终止条件时停止模拟。下面是一种基于迭代的解题思路和设计：
解题思路：

初始化：创建一个包含n个人初始编号的列表，并初始化一个变量表示当前位置。
循环删除过程：

在当前位置开始数m个人。
计算出要删除的人的位置。
从列表中删除该位置的人。
更新当前位置为删除位置。

终止条件：当剩下的人数满足终止条件时，停止循环。
返回结果：根据具体要求返回结果。在约瑟夫问题中，通常是返回最后剩下的一个人的编号或一组编号。

3. 代码实现

3.1 代码实现一

30 个人在一条船上，超载，需要 15 人下船。于是人们排成一队，排队的位置即为他们的编号。报数，从 1 开始，数到 9 的人下船。如此循环，直到船上人不能数到9人为止，问剩下的人的编号？

def josephus(n, m):# 创建一个列表，表示n个人的初始编号people = list(range(1, n + 1))# 初始化变量，表示当前位置current = 0# 循环，直到剩下8个人while len(people) > 8:# 计算下一个要删除的人的位置current = (current + m - 1) % len(people)# 删除当前位置的人del people[current]# 返回剩下的最后一个人的编号return people# 示例：有30个人，每次数9个人
result = josephus(30, 9)
print("最后剩下的人的编号是:", result)

运行效果：

3.2 代码实现二

题目修改为：
30 个人在一条船上，超载，需要 15 人下船。于是人们排成一队，排队的位置即为他们的编号。报数，从 1 开始，数到 9 的人下船。如此循环，直到船上仅剩 15 人为止，问剩下的人的编号？

def josephus(n, m, k):# 创建一个包含n个人初始编号的列表people = list(range(1, n + 1))# 初始化变量，表示当前位置current = 0# 循环，直到剩下的人数满足终止条件while len(people) > k:# 在当前位置开始数m个人，计算出要删除的人的位置current = (current + m - 1) % len(people)# 从列表中删除该位置的人del people[current]# 返回剩下的人的编号return people# 示例：有30个人，每次数9个人删除，直至剩下15个人
result = josephus(30, 9, 15)
print("剩下的人的编号是:", result)

3.3 代码实现三

题目修改为：
30 个人在一条船上，超载，需要 15 人下船。于是人们排成一队，排队的位置即为他们的编号。报数，从 5 开始，数到 9 的人下船。如此循环，直到船上仅剩 15 人为止，问剩下的人的编号？

def josephus_with_start(n, m, k, start):people = list(range(1, n + 1))current = start - 1  # 起始位置while len(people) > k:current = (current + m - 1) % len(people)del people[current]return people# 示例：有30个人，每次数9个人删除，直至剩下15个人，起始位置为5
result = josephus_with_start(30, 9, 15, 5)
print("剩下的人的编号是:", result)

3.4 代码实现四

题目修改为：
30 个人在一条船上，超载，需要 15 人下船。于是人们排成一队，排队的位置即为他们的编号。报数，从 1 开始，数到 9 的人下船，但是每隔一轮人才下船。如此循环，直到船上仅剩 15 人为止，问剩下的人的编号？

def josephus_with_custom_deletion(n, m, k, deletion_rule):people = list(range(1, n + 1))current = 0while len(people) > k:current = deletion_rule(current, m, len(people))del people[current]return people# 示例：有30个人，每次数9个人删除，直至剩下15个人，但是每隔一轮删除一个人
def custom_deletion_rule(current, m, length):return (current + m) % lengthresult = josephus_with_custom_deletion(30, 9, 15, custom_deletion_rule)
print("剩下的人的编号是:", result)