计算方法 c++代码

环境：Windows 10 + Dev-C++ 5.11

Lagrange 插值方法

Lagrange 插值多项式：在这里插入图片描述

#include<bits/stdc++.h>
using namespace std;
#define int long long
#define fer(i,a,b) for(int i=a;i<b;i++)
signed main(){cout<<"拉格朗日插值法，请输入插值点个数n：";int n;cin>>n;printf("请输入%d个插值点x值（等距）：",n);double fx[n],x[n];fer(i,0,n){cin>>x[i];}//{24 26 28 30}{1.888175 1.918645 1.947294 1.961009};printf("请输入%d个插值点f(x)值：",n);fer(i,0,n){cin>>fx[i];}int m;printf("请输入待求点个数m：");cin>>m; double targetx[m];//{25 27 29};printf("请输入%d个待求点x值：",m);fer(i,0,m){cin>>targetx[i];}double phi[n];//系数for(int i=0;i<m;i+=1){fer(j,0,n)phi[j]=1;//初始化fer(j,0,n){fer(k,0,n){if(j!=k){phi[j]*=(targetx[i]-x[k]);phi[j]/=(x[j]-x[k]);}}}double res=0;  fer(j,0,n){res+=phi[j]*fx[j];//cout<<i<<" "<<phi[i]<<" "<<data[i]<<" "<<res<<endl;}cout<<"x="<<targetx[i]<<" , L(x)="<<res<<endl;}return 0;
}

牛顿插值方法

#include<bits/stdc++.h>
using namespace std;
#define int long long
#define fer(i,a,b) for(int i=a;i<b;i++)
signed main(){cout<<"牛顿插值法，请输入插值点个数n：";int n;cin>>n;double data[n];//={0.41075 0.57815 0.69675 0.88811 1.02652};double a[n];//={0.4 0.55 0.65 0.8 0.9};printf("请输入%d个插值点x值：",n);fer(i,0,n){cin>>a[i];}printf("请输入%d个插值点f(x)值：",n);fer(i,0,n){cin>>data[i];}double dp[n][n+1];fer(i,0,n){dp[i][0]=a[i];dp[i][1]=data[i];}fer(j,2,n+1){fer(i,j-1,n){dp[i][j]=(dp[i][j-1]-dp[i-1][j-1])/(dp[i][0]-dp[i-j+1][0]);}}cout<<"差商结果如下："<<endl;cout<<"x        f(x)     ";fer(i,0,n-1)cout<<i+1<<"阶差商  ";cout<<endl;fer(i,0,n){fer(j,0,i+2){cout<<left<<setw(9)<<dp[i][j]<<" ";}cout<<endl;}cout<<"请输入待求点个数m：";int m;cin>>m;double targetx[m];printf("请输入%d个待求点x值：",m);//0.895fer(i,0,m){cin>>targetx[i];}for(int x=0;x<m;x++){double res=0;double now;fer(i,0,n){now=dp[i][i+1];fer(j,0,i){now*=(targetx[x]-a[j]);}res+=now;}cout<<"x="<<targetx[x]<<" , p(x)="<<res<<endl;}return 0;
}

Newton-Cotes 方法

计算以下积分值：
在这里插入图片描述

#include<bits/stdc++.h>
using namespace std;
#define int long long
#define fer(i,a,b) for(int i=a;i<b;i++)
#define E  2.7182818284590452354
double trapezoid(double down,double up,double fx[]){//积分下限、上限、插值点 //梯形求积公式double res=(up-down)/2;res*=(fx[0]+fx[1]);return res;
}
double simpson(double down,double up,double fx[]){double res=(up-down)/6;res*=(fx[0]+4*fx[1]+fx[2]);return res;
}
double cotes(double down,double up,double fx[]){double res=(up-down)/90;res*=(7*fx[0]+32*fx[1]+12*fx[2]+32*fx[3]+7*fx[4]);return res;
}
double fx1(double x){double res=4-sin(x)*sin(x);res=sqrt(res);return res;
}
double fx2(double x){if(x==0)return 1;double res=sin(x)/x;return res;
}
double fx3(double x){double res=pow(E,x);res/=(4+x*x);return res;
}
double fx4(double x){double res=log(1+x);res/=(1+x*x);return res;
}
signed main(){cout<<"牛顿-柯特斯公式"<<endl;cout<<"积分1:f(x)=sqrt(4-sin(x)^2)"<<endl;cout<<"请输入积分下限和上限（小数输入）:";double a,b;cin>>a>>b;cout<<"当求积节点个数=2时，使用梯形求积公式，积分结果为：";double trapex[2],trapefx[2];trapex[0]=a;trapex[1]=b;fer(i,0,2){trapefx[i]=fx1(trapex[i]);}double res=trapezoid(a,b,trapefx);cout<<setprecision(16)<<res<<endl;cout<<"当求积节点个数=3时，使用辛普森求积公式，积分结果为：";double simpsonx[3],simpsonfx[3];simpsonx[0]=a;simpsonx[1]=(a+b)/2;simpsonx[3]=b;fer(i,0,3){simpsonfx[i]=fx1(simpsonx[i]);}res=simpson(a,b,simpsonfx);cout<<setprecision(16)<<res<<endl;cout<<"当求积节点个数=5时，使用柯特斯求积公式，积分结果为：";double cotesx[5],cotesfx[5];cotesx[0]=a;cotesx[1]=(a+b)/4;cotesx[2]=(a+b)/2;cotesx[3]=(a+b)/4*3;cotesx[4]=b;fer(i,0,5){cotesfx[i]=fx1(cotesx[i]);}res=cotes(a,b,cotesfx);cout<<setprecision(16)<<res<<endl<<endl;cout<<"积分2:f(x)=sinx/x"<<endl;cout<<"请输入积分下限和上限（小数输入）:";cin>>a>>b;cout<<"当求积节点个数=2时，使用梯形求积公式，积分结果为：";trapex[0]=a;trapex[1]=b;fer(i,0,2){trapefx[i]=fx2(trapex[i]);}res=trapezoid(a,b,trapefx);cout<<setprecision(16)<<res<<endl;cout<<"当求积节点个数=3时，使用辛普森求积公式，积分结果为：";simpsonx[0]=a;simpsonx[1]=(a+b)/2;simpsonx[3]=b;fer(i,0,3){simpsonfx[i]=fx2(simpsonx[i]);}res=simpson(a,b,simpsonfx);cout<<setprecision(16)<<res<<endl;cout<<"当求积节点个数=5时，使用柯特斯求积公式，积分结果为：";cotesx[0]=a;cotesx[1]=(a+b)/4;cotesx[2]=(a+b)/2;cotesx[3]=(a+b)/4*3;cotesx[4]=b;sfer(i,0,5){cotesfx[i]=fx2(cotesx[i]);}res=cotes(a,b,cotesfx);cout<<setprecision(16)<<res<<endl<<endl;cout<<"积分3:f(x)=e^x/(4+x^2)"<<endl;cout<<"请输入积分下限和上限（小数输入）:";cin>>a>>b;cout<<"当求积节点个数=2时，使用梯形求积公式，积分结果为：";trapex[0]=a;trapex[1]=b;fer(i,0,2){trapefx[i]=fx3(trapex[i]);}res=trapezoid(a,b,trapefx);cout<<setprecision(16)<<res<<endl;cout<<"当求积节点个数=3时，使用辛普森求积公式，积分结果为：";simpsonx[0]=a;simpsonx[1]=(a+b)/2;simpsonx[3]=b;fer(i,0,3){simpsonfx[i]=fx3(simpsonx[i]);}res=simpson(a,b,simpsonfx);cout<<setprecision(16)<<res<<endl;cout<<"当求积节点个数=5时，使用柯特斯求积公式，积分结果为：";cotesx[0]=a;cotesx[1]=(a+b)/4;cotesx[2]=(a+b)/2;cotesx[3]=(a+b)/4*3;cotesx[4]=b;fer(i,0,5){cotesfx[i]=fx3(cotesx[i]);}res=cotes(a,b,cotesfx);cout<<setprecision(16)<<res<<endl<<endl;cout<<"积分4:f(x)=ln(1+x)/(1+x^2)"<<endl;cout<<"请输入积分下限和上限（小数输入）:";cin>>a>>b;cout<<"当求积节点个数=2时，使用梯形求积公式，积分结果为：";trapex[0]=a;trapex[1]=b;fer(i,0,2){trapefx[i]=fx4(trapex[i]);}res=trapezoid(a,b,trapefx);cout<<setprecision(16)<<res<<endl;cout<<"当求积节点个数=3时，使用辛普森求积公式，积分结果为：";simpsonx[0]=a;simpsonx[1]=(a+b)/2;simpsonx[3]=b;fer(i,0,3){simpsonfx[i]=fx4(simpsonx[i]);}res=simpson(a,b,simpsonfx);cout<<setprecision(16)<<res<<endl;cout<<"当求积节点个数=5时，使用柯特斯求积公式，积分结果为：";cotesx[0]=a;cotesx[1]=(a+b)/4;cotesx[2]=(a+b)/2;cotesx[3]=(a+b)/4*3;cotesx[4]=b;fer(i,0,5){cotesfx[i]=fx4(cotesx[i]);}res=cotes(a,b,cotesfx);cout<<setprecision(16)<<res<<endl<<endl;return 0;
}

求非线性方程根的牛顿法

用牛顿迭代法求 xe^x − 1 = 0 的根，迭代初始值为 x0 = 0.5。

#include<bits/stdc++.h>
using namespace std;
#define int long long
#define fer(i,a,b) for(int i=a;i<b;i++)
signed main(){cout<<"牛顿迭代法，所求方程为：xe^x-1=0"<<endl;cout<<"请输入初值：";double x;cin>>x;cout<<"请输入最大迭代次数:";int n;cin>>n;cout<<"请输入精度要求：";double epsilon;cin>>epsilon;bool flag=0;for(int i=0;i<n;i++){double f=x*exp(x)-1;double df=exp(x)+x*exp(x);double x1=x-f/df;cout<<"第"<<i+1<<"次迭代，x="<<x1<<endl;if(abs(x1-x)<epsilon){cout<<"精度已达要求"<<endl;flag=1;break;}x=x1;}if(flag==0)cout<<"迭代次数已达上限"<<endl;return 0;
}

高斯-赛德尔迭代法解线性方程组

#include<bits/stdc++.h>
using namespace std;
#define int long long
#define fer(i,a,b) for(int i=a;i<b;i++)signed main(){cout<<"Gauss-Seidel迭代法解线性方程组"<<endl;cout<<"请输入矩阵维数n:";int n;cin>>n;double a[n][n],b[n];cout<<"请输入增广矩阵("<<n<<"x"<<n+1<<"):";fer(i,0,n){fer(j,0,n){cin>>a[i][j];}cin>>b[i];}cout<<"请输入迭代初值向量:";double x[n];fer(i,0,n)cin>>x[i];cout<<"请输入精度要求：";double epsilon;cin>>epsilon;cout<<"请输入最大迭代次数:";int m;cin>>m;double phi[n][n];fer(i,0,n){fer(j,0,n){if(j==i)phi[i][j]=0;else{phi[i][j]=-a[i][j]/a[i][i];}}}// 10 -1 -2 7.2  -1 10 -2 8.3  -1 -1 5 4.2bool flag=0;double x1[n];fer(k,0,m){fer(i,0,n){x1[i]=b[i]/a[i][i];fer(j,0,n){x1[i]+=phi[i][j]*x[j];}if(abs(x1[i]-x[i])<epsilon){flag=1;break;}x[i]=x1[i];}cout<<"第"<<k+1<<"次迭代，x=[";fer(i,0,n){cout<<setprecision(10)<<x[i];
if(i!=n-1)cout<<"  ";}cout<<"]"<<endl;if(flag){cout<<"精度已达要求"<<endl;break;}}if(flag==0)cout<<"迭代次数已达上限"<<endl;return 0;
}

高斯消元法求解线性方程组

#include<bits/stdc++.h>
using namespace std;
#define int long long
#define fer(i,a,b) for(int i=a;i<b;i++)
#define E  2.7182818284590452354
signed main(){cout<<"高斯消元法"<<endl;cout<<"请输入矩阵维数n:";int n;cin>>n;double a[n][n],b[n];cout<<"请输入增广矩阵("<<n<<"x"<<n+1<<"):";fer(i,0,n){fer(j,0,n){cin>>a[i][j];}cin>>b[i];}   // 10 -1 -2 7.2  -1 10 -2 8.3  -1 -1 5 4.2double phi;fer(k,0,n-1){//用于消元的行 fer(i,k+1,n){//被消元的行 phi=-a[i][k]/a[k][k];//消元系数 fer(j,k,n){a[i][j]+=phi*a[k][j];}b[i]+=phi*b[k];}}double x[n];for(int i=n-1;i>=0;i--){ x[i]=b[i];fer(j,i+1,n){x[i]-=a[i][j]*x[j];}x[i]/=a[i][i];}cout<<"x=[";fer(i,0,n){cout<<x[i]; if(i!=n-1)cout<<" ";}cout<<"]"<<endl;return 0;
}

Doolittle 分解法求解线性方程组

#include<bits/stdc++.h>
using namespace std;
#define int long long
#define fer(i,a,b) for(int i=a;i<b;i++)signed main(){cout<<"Doolittle分解法解线性方程组"<<endl;cout<<"请输入矩阵维数n:";int n;cin>>n;double a[n][n],b[n];cout<<"请输入增广矩阵("<<n<<"x"<<n+1<<"):";fer(i,0,n){fer(j,0,n){cin>>a[i][j];}cin>>b[i];}double l[n][n],u[n][n];fer(i,0,n){fer(j,0,i)u[i][j]=0;fer(j,i,n){u[i][j]=a[i][j];fer(k,0,i){u[i][j]-=l[i][k]*u[k][j];}}fer(j,0,i)l[j][i]=0;l[i][i]=1;fer(j,i+1,n){//计算L,j是行标 l[j][i]=a[j][i];fer(k,0,i){l[j][i]-=l[j][k]*u[k][i];}l[j][i]/=u[i][i];}}cout<<"L="<<endl;fer(i,0,n){fer(j,0,n)cout<<setw(10)<<l[i][j]<<" ";cout<<endl;}cout<<"U="<<endl;fer(i,0,n){fer(j,0,n)cout<<setw(10)<<u[i][j]<<" ";cout<<endl;}double y[n];fer(i,0,n){//Ly=b,求y y[i]=b[i];fer(j,0,i)y[i]-=l[i][j]*y[j];}double x[n];for(int i=n-1;i>=0;i--){x[i]=y[i];fer(j,i+1,n){x[i]-=u[i][j]*x[j];}x[i]/=u[i][i];}cout<<"x=[";fer(i,0,n){cout<<setprecision(10)<<x[i];if(i!=n-1)cout<<"  ";}cout<<"]"<<endl;// 10 -1 -2 7.2  -1 10 -2 8.3  -1 -1 5 4.2return 0;
}

欧拉法求解常微分方程

使用常微分方程例子如下：
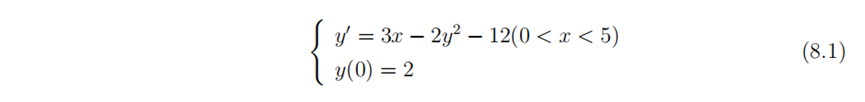
在这里插入图片描述

#include<bits/stdc++.h>
using namespace std;
#define int long long
#define fer(i,a,b) for(int i=a;i<b;i++)
double f(double x,double y){return 3*x-2*y*y-12;
}
signed main(){cout<<"求解常微分方程，方程：y'=3x-2y^2-12"<<endl; double x,y,h;cout<<"请输入初值x,f(x)：";cin>>x>>y;cout<<"请输入步长h：";cin>>h;cout<<"请输入x上限：";double n;cin>>n;int k=n/h; cout<<"欧拉法:"<<endl;double x1=x,y1=y;cout<<"f("<<x1<<")="<<y1<<endl;fer(i,0,k){double fxy=f(x1,y1);x1+=h;y1=y1+h*fxy;cout<<"f("<<x1<<")="<<y1<<endl;}cout<<endl<<"改进的欧拉法:"<<endl; x1=x;y1=y;cout<<"f("<<x1<<")="<<y1<<endl;fer(i,0,k){double forcasty=y1+h*f(x1,y1);y1=y1+h/2.0*(f(x1,y1)+f(x1+h,forcasty));x1+=h;cout<<"f("<<x1<<")="<<y1<<endl;}return 0;
}