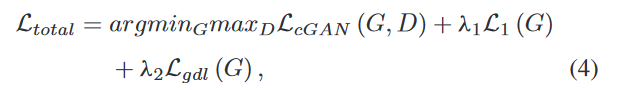目录
一,最长等差子序列
1.题目
2.题目接口
3.解题思路及其代码
二,等差序列的划分——子序列
1.题目
2.题目接口
3.解题思路及其代码
一,最长等差子序列
1.题目
给你一个整数数组
nums,返回nums中最长等差子序列的长度。回想一下,
nums的子序列是一个列表nums[i1], nums[i2], ..., nums[ik],且0 <= i1 < i2 < ... < ik <= nums.length - 1。并且如果seq[i+1] - seq[i](0 <= i < seq.length - 1) 的值都相同,那么序列seq是等差的。示例 1:
输入:nums = [3,6,9,12] 输出:4 解释: 整个数组是公差为 3 的等差数列。示例 2:
输入:nums = [9,4,7,2,10] 输出:3 解释: 最长的等差子序列是 [4,7,10]。示例 3:
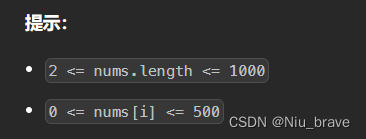
输入:nums = [20,1,15,3,10,5,8] 输出:4 解释: 最长的等差子序列是 [20,15,10,5]。提示:
2 <= nums.length <= 10000 <= nums[i] <= 500
2.题目接口
class Solution {
public:int longestArithSeqLength(vector<int>& nums) {}
};3.解题思路及其代码
1.状态转移方程:
每次做动态规划问题时都要先找到状态转移方程。在这道题里面,我们要找的是最长的等差子序列,那我们的状态转移方程必须就是二维的,为什么呢?因为要找等差序列我们首先得找到差值,一个数是构成不了差的只有两个数才行。现在我规定:dp[i][j]表示以arr[i]和arr[j]为结尾的等差子序列的最大长度,差值为arr[j]-arr[i]。那我们的dp[i][j] = dp[k][i]+1。其中dp[k][i]也表示以arr[k],arr[i]为结尾的最长的等差子序列。
2.初始化:
因为:
所以这道题的子序列最小长度就应该为2。所以在初始化时可以初始化为2。
3.优化:
这道题的优化点还是在与元素与下标数组或者下标的绑定。
先来看第一种:
元素与下标数组的绑定(要与下标数组绑定的原因在于元素的出现次数会重复)
操作如下:
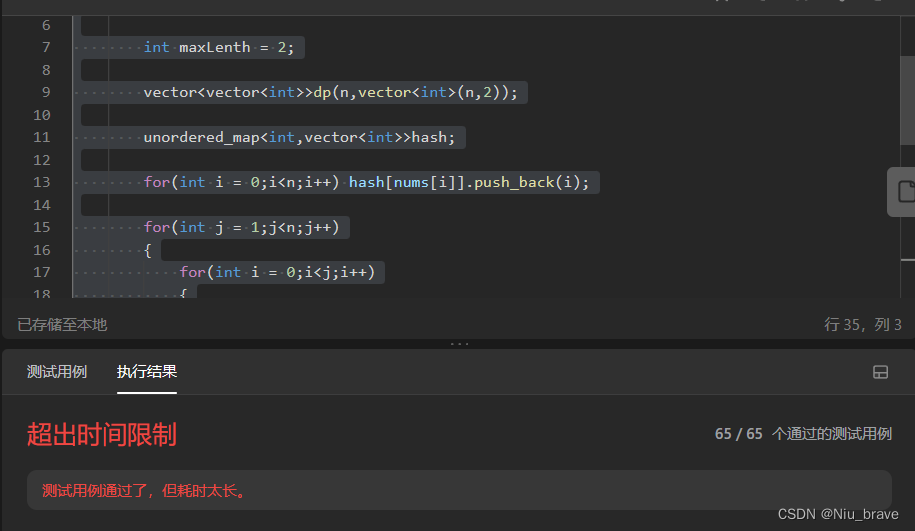
vector<vector<int>>dp(n,vector<int>(n,2));unordered_map<int,vector<int>>hash;for(int i = 0;i<n;i++) hash[nums[i]].push_back(i);但是在这道题里面如果按照上面的方式绑定的话,就会面临一个超时的问题。如下:
class Solution { public:int longestArithSeqLength(vector<int>& nums) {int n = nums.size();int maxLenth = 2;vector<vector<int>>dp(n,vector<int>(n,2));unordered_map<int,vector<int>>hash;for(int i = 0;i<n;i++) hash[nums[i]].push_back(i);for(int j = 1;j<n;j++){for(int i = 0;i<j;i++){int num = 2*nums[i]-nums[j];for(auto e:hash[num]){if(e<i){dp[i][j] = dp[e][i]+1;}}maxLenth = max(maxLenth,dp[i][j]);}}return maxLenth;} };结果如下:
第二种优化方法:
元素与下标进行绑定。
前面说了,这道题里面是有重复元素的。如果直接初始化hash表就会出现下标覆盖的问题。所以在这里初始化下标就得来点技巧:
1.先初始化hash[nums[0]] = 0;
unordered_map<int,int>hash;hash[nums[0]] = 0;2.先固定倒数第二个位置,遍历倒数第一个位置。(这样填表的目的就是为了在出现重复元素的时候能把离i最近的元素代入二不管其它元素)。
3.在遍历完i前面的元素以后才把hash[nums[i]]与i进行绑定。为什么呢?因为i下标肯定不是在i的前面的。并且,如果你在之前就将hash表就全部初始化了的话就会有覆盖问题。覆盖问题会导致在以i,j位置为结尾的等差序列本来是可以和前面的重复元素结成等差子序列的,但是因为下标覆盖问题导致我下标竟然比前面的元素小进而导致错误。
代码如下:
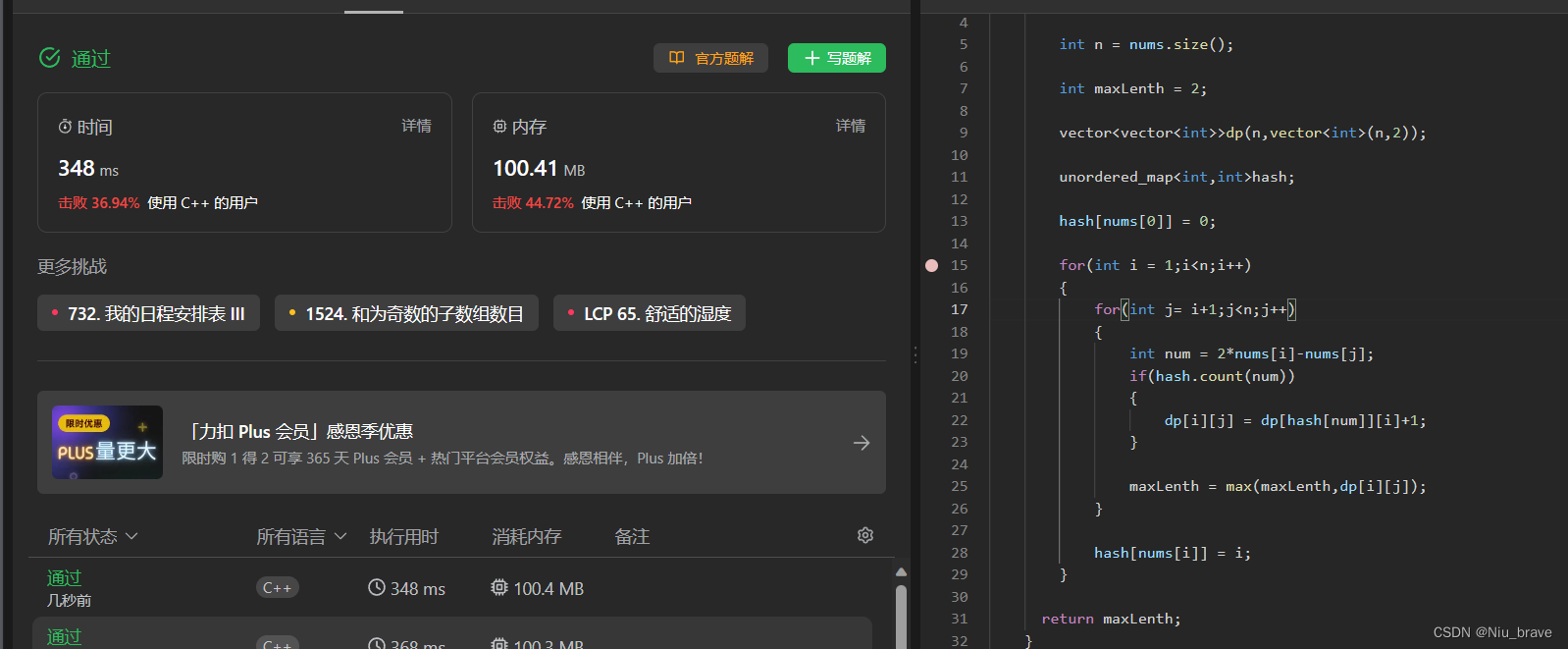
class Solution { public:int longestArithSeqLength(vector<int>& nums) {int n = nums.size();int maxLenth = 2;vector<vector<int>>dp(n,vector<int>(n,2));unordered_map<int,int>hash;hash[nums[0]] = 0;for(int i = 1;i<n;i++){for(int j= i+1;j<n;j++){int num = 2*nums[i]-nums[j];if(hash.count(num)){dp[i][j] = dp[hash[num]][i]+1;}maxLenth = max(maxLenth,dp[i][j]);}hash[nums[i]] = i;}return maxLenth;} };结果:
二,等差序列的划分——子序列
1.题目
给你一个整数数组
nums,返回nums中所有 等差子序列 的数目。如果一个序列中 至少有三个元素 ,并且任意两个相邻元素之差相同,则称该序列为等差序列。
- 例如,
[1, 3, 5, 7, 9]、[7, 7, 7, 7]和[3, -1, -5, -9]都是等差序列。- 再例如,
[1, 1, 2, 5, 7]不是等差序列。数组中的子序列是从数组中删除一些元素(也可能不删除)得到的一个序列。
- 例如,
[2,5,10]是[1,2,1,2,4,1,5,10]的一个子序列。题目数据保证答案是一个 32-bit 整数。
示例 1:
输入:nums = [2,4,6,8,10] 输出:7 解释:所有的等差子序列为: [2,4,6] [4,6,8] [6,8,10] [2,4,6,8] [4,6,8,10] [2,4,6,8,10] [2,6,10]示例 2:
输入:nums = [7,7,7,7,7] 输出:16 解释:数组中的任意子序列都是等差子序列。提示:
1 <= nums.length <= 1000-231 <= nums[i] <= 231 - 1
2.题目接口
class Solution {
public:int numberOfArithmeticSlices(vector<int>& nums) {}
};3.解题思路及其代码
这道题的解题思路和前面的题目的思路差不多,只是dp[i][j]的所表示的意义不同了。这里的dp[i][j]表示以arr[i],arr[j]为结尾的子序列的个数。代码如下:
class Solution { public:int numberOfArithmeticSlices(vector<int>& nums) {int n = nums.size();vector<vector<int>>dp(n,vector<int>(n));//这次表示的是以i,j下标为结尾的最大个数unordered_map<long long ,vector<long long>>hash;//使用long long是因为数据太大会溢出for(int i = 0;i<n;i++) hash[nums[i]].push_back(i);//元素+下标数组绑定是因为有重复元素。int count = 0;for(int j = 2;j<n;j++){for(int i= 1;i<j;i++){long long num =(long long) 2*nums[i] - (long long)nums[j];//使用long long是因为数据太大会溢出for(auto e:hash[num]){if(e<i){dp[i][j]+= dp[e][i]+1;//找前面的子序列的个数再加上自己这个新的。}else{break;//因为vector是尾插,所以出现重复元素时下标小的在前面。}}count+=dp[i][j];//统计所有等差子序列的个数}}return count;} };