1 文本格式
/// <summary>
/// 比较a,b的大小,返回1,0,-1
/// 数据从低位(右)往高位(左)存储;
/// </summary>
/// <param name="a"></param>
/// <param name="b"></param>
/// <returns></returns>
public static int big_integer_compare(int[] a, int[] b)
{
for (int i = a.Length - 1; i >= 0; i--)
{
if (a[i] > b[i]) return 1;
else if (a[i] < b[i]) return -1;
}
//两位数相等
return 0;
}
/// <summary>
/// 《小白学程序》第二十三课:大数(BigInteger)的四则运算之四,除法
/// 大数除法 c = a / b % d
/// c 为商,d 为余数。
/// 网上常见的除法算法是:用“被除数”不断地减去“除数”,减去的“次数”就是商,剩下的就是余数。
/// 这当然很慢慢慢慢慢慢慢慢慢慢慢慢慢慢慢慢慢慢慢慢慢慢慢慢慢慢慢慢慢慢慢慢慢慢慢慢慢慢慢
/// 本文发布的是纯加、减法实现的 Truffer 大数除法。
/// Truffer 大数除法的核心思想是按两个数的位数差距,估算一个倍数,比如10000,再进行减法计算;
/// 以此类推计算剩余的数字。
/// </summary>
/// <param name="a"></param>
/// <param name="b"></param>
/// <param name="d">余数</param>
/// <returns>商c</returns>
public static string big_integer_divide(string a, string b, out string d)
{
int n = a.Length;
int[] db = string_to_digitals(b, n);
string q = a;
List<string> p = new List<string>();
int[] dq = string_to_digitals(q, n);
while (big_integer_compare(dq, db) >= 0)
{
// 按相差的位数构造 100... 这样的倍数,作为 被减的数的倍数。
int len = q.Length - b.Length;
// 被减数 = 倍数 * 除数
string v2 = b + String.Join("", new int[len]);
int[] dv = string_to_digitals(v2, n);
// 如果当前数与被减数长度系统,调整倍数
if (big_integer_compare(dq, dv) < 0)
{
len--;
v2 = b + String.Join("", new int[len]);
dv = string_to_digitals(v2, n);
}
// 每次减去一次被减数,并记录倍数;
string v1 = "1" + String.Join("", new int[len]);
while (big_integer_compare(dq, dv) >= 0)
{
p.Add(v1);
q = big_integer_subtract(q, v2);
dq = string_to_digitals(q, n);
}
}
// 最后剩下的就是 余数!
d = q;
// 记录的 被减倍数 之和就是 商
string r = p[0];
for (int i = 1; i < p.Count; i++)
{
r = big_integer_plus(r, p[i]);
}
return r;
}
2 代码格式
/// <summary>
/// 比较a,b的大小,返回1,0,-1
/// 数据从低位(右)往高位(左)存储;
/// </summary>
/// <param name="a"></param>
/// <param name="b"></param>
/// <returns></returns>
public static int big_integer_compare(int[] a, int[] b)
{for (int i = a.Length - 1; i >= 0; i--){if (a[i] > b[i]) return 1;else if (a[i] < b[i]) return -1;}//两位数相等return 0;
}/// <summary>
/// 《小白学程序》第二十三课:大数(BigInteger)的四则运算之四,除法
/// 大数除法 c = a / b % d
/// c 为商,d 为余数。
/// 网上常见的除法算法是:用“被除数”不断地减去“除数”,减去的“次数”就是商,剩下的就是余数。
/// 这当然很慢慢慢慢慢慢慢慢慢慢慢慢慢慢慢慢慢慢慢慢慢慢慢慢慢慢慢慢慢慢慢慢慢慢慢慢慢慢慢
/// 本文发布的是纯加、减法实现的 Truffer 大数除法。
/// Truffer 大数除法的核心思想是按两个数的位数差距,估算一个倍数,比如10000,再进行减法计算;
/// 以此类推计算剩余的数字。
/// </summary>
/// <param name="a"></param>
/// <param name="b"></param>
/// <param name="d">余数</param>
/// <returns>商c</returns>
public static string big_integer_divide(string a, string b, out string d)
{int n = a.Length;int[] db = string_to_digitals(b, n);string q = a;List<string> p = new List<string>();int[] dq = string_to_digitals(q, n);while (big_integer_compare(dq, db) >= 0){// 按相差的位数构造 100... 这样的倍数,作为 被减的数的倍数。int len = q.Length - b.Length;// 被减数 = 倍数 * 除数string v2 = b + String.Join("", new int[len]);int[] dv = string_to_digitals(v2, n);// 如果当前数与被减数长度系统,调整倍数if (big_integer_compare(dq, dv) < 0){len--;v2 = b + String.Join("", new int[len]);dv = string_to_digitals(v2, n);}// 每次减去一次被减数,并记录倍数;string v1 = "1" + String.Join("", new int[len]);while (big_integer_compare(dq, dv) >= 0){p.Add(v1);q = big_integer_subtract(q, v2);dq = string_to_digitals(q, n);}}// 最后剩下的就是 余数!d = q;// 记录的 被减倍数 之和就是 商string r = p[0];for (int i = 1; i < p.Count; i++){r = big_integer_plus(r, p[i]);}return r;
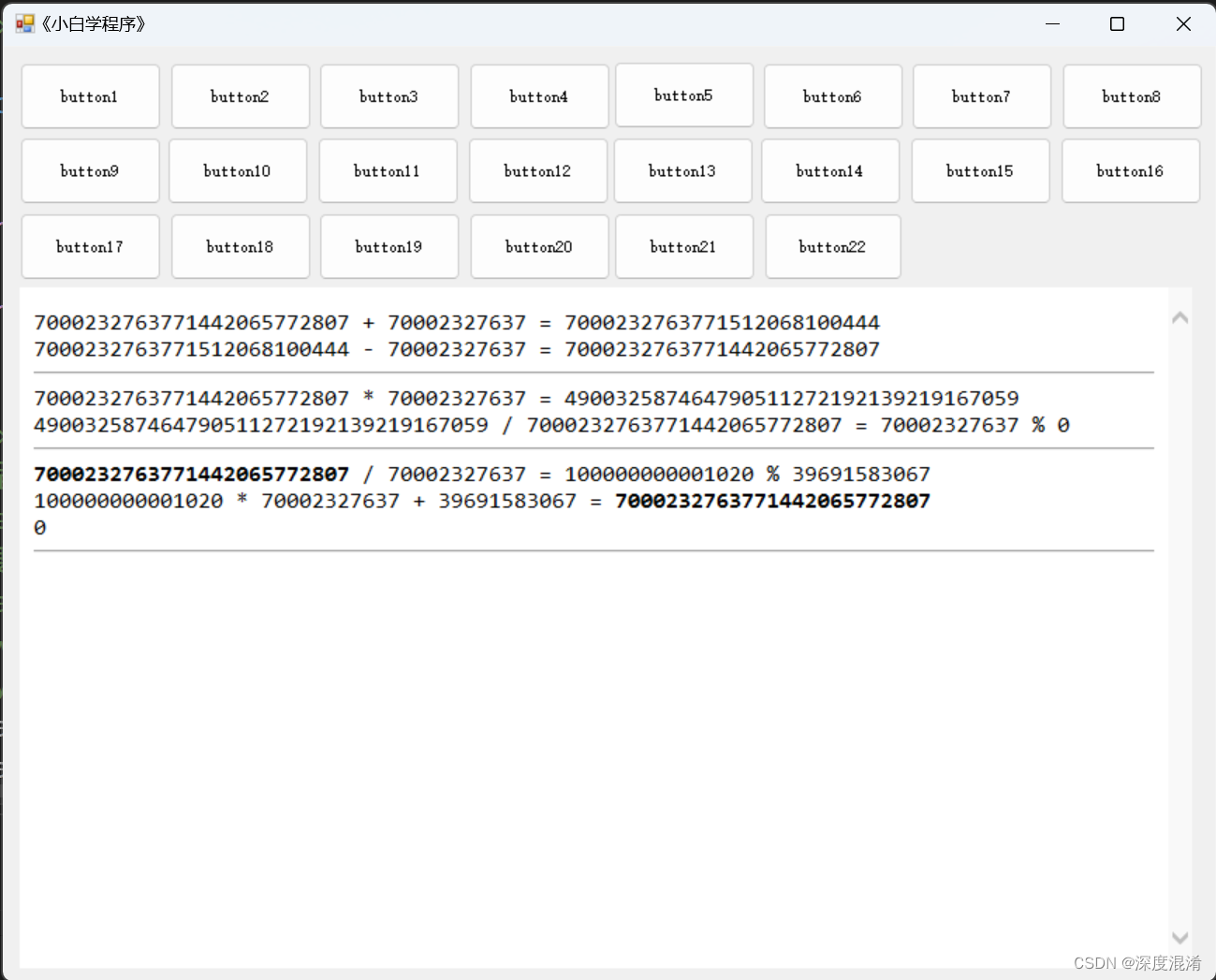
}3 计算结果




![[ACTF2020 新生赛]BackupFile](https://img-blog.csdnimg.cn/009c3f6e028d49dfbca3e27152996019.png)