CSA

简介：Chirp Scaling 算法 (简称 CS 算法，即 CSA) 避免了 RCMC 中的插值操作。该算法基于 Scaling 原理，通过对 chirp 信号进行频率调制，实现了对信号的尺度变换或平移。基于这种原理，可以通过相位相乘代替时域插值来完成随距离变化的RCMC。此外，由于需要在二维频域进行数据处理，CSA 还能解决 SRC 对方位频率的依赖问题。

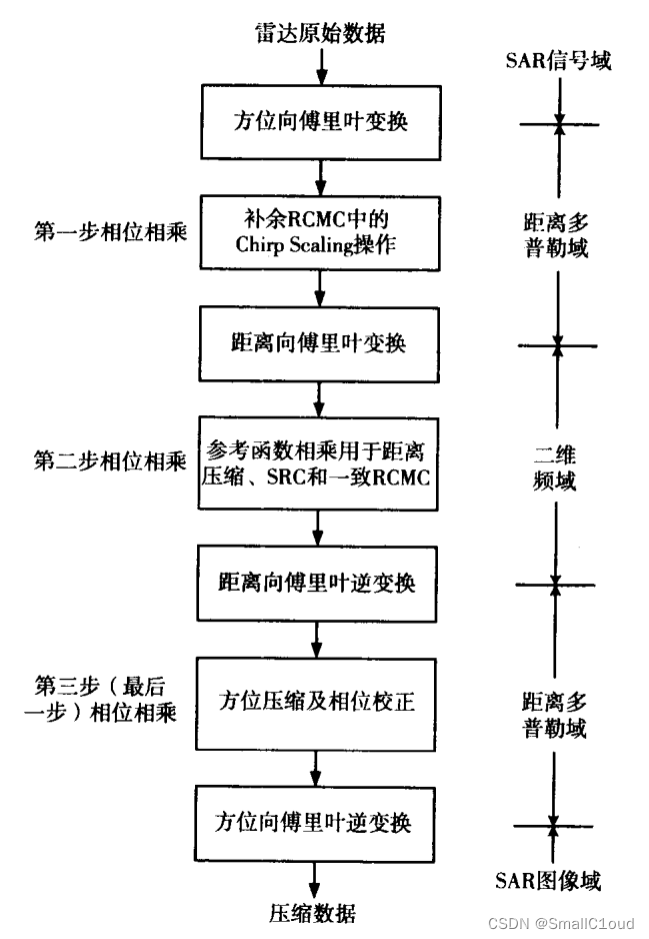
1. 通过方位向 FFT 将数据变换到距离多普勒域。
2. 通过相位相乘实现 Chirp Scaling 操作，使所有目标的距离徙动轨迹一致化。
3. 通过距离向 FFT 将数据变换到二维频域。
4. 与参考函数进行相位相乘，同时完成距离压缩、SRC 和一致 RCMC。
5. 通过距离向 IFFT 将数据变换回距离多普勒域。
6. 通过与随距离变化的匹配滤波器进行相位相乘，实现方位压缩。(由于步骤 2中的 Chirp Scaling 操作，相位相乘时需要进行相位矫正)
7. 方位向 IFFT 将数据变换回二维时域。

数据分析

本次使用的是RADARSAT-1原始数据，该数据采集于2002年6月16日，照射的是加拿大温哥华地区。数据储存在 data_01.001 文件中，包含近19400条记录，每八条记录包含一条传输脉冲的复制信号。每条距离线有9288个复回波采样点，按照uint类型存储。除去复制信号，该记录共18818字节，先是192字节头信息和50字节辅助信息，然后是18576字节回波数据。

参数设置

采样率：$F_r=32.317MHz$

脉冲宽度：$T_p=30.111MHz$

距离向调频率：$F_r=0.72135MHz/\mu s$

数据窗开始时间：$6.5956ms$

脉宽：$T_r=41.74\mu s$

复制信号采样数：1349

每回波行采样数：9280

雷达频率：$f_0=5.3GHz$

雷达波长：$\lambda =0.05657m$

脉冲重复频率：$F_a=1256.98Hz$

有效雷达速率：$V_r=7062m/s$

方位向调频率：$K_a=1733Hz/s$

多普勒中心频率：$f_{{\eta }_c}=-6900Hz$

参考步骤

处理细节

本次仿真中，用到的傅里叶变换及傅里叶逆变换均采取如下方法

X = fftshift(fft(fftshift(x)));		%傅里叶变换x = ifftshift(ifft(ifftshift(X)));	%逆傅里叶变换

这样做的好处是变换后频率范围为$-\pi$ ~ $\pi$。

成像结果

示例

下图给出了本次实验数据所成的SAR图像示例，其斜距分辨率为6m，地面分辨率为10m，单视对全方位带宽进行处理，相应的分辨率为9m。

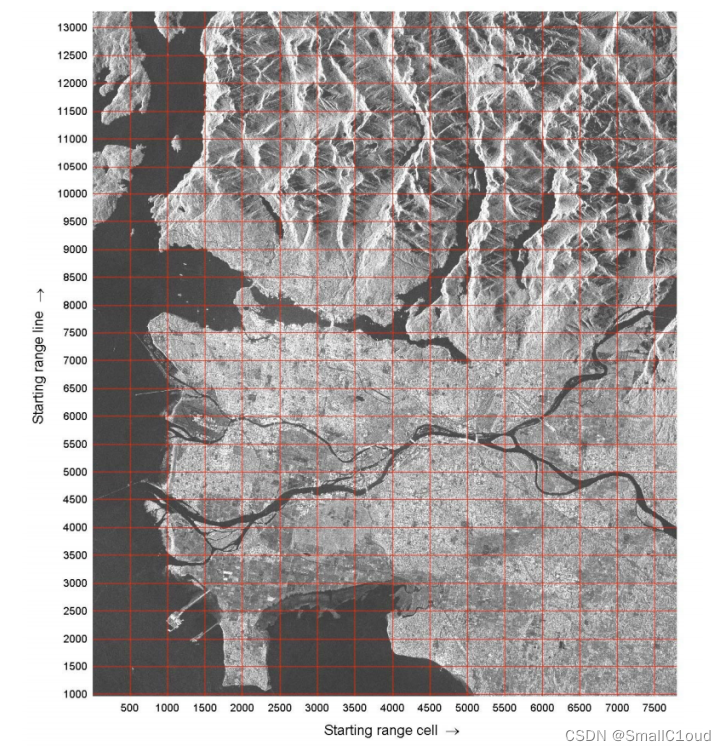
1536×2048

本次实验首先从文件DAT_01.001中提取了7769 ~ 9306行、1050 ~ 3098列共1536×2048的数据储存到文件CDdata1.mat中；9307~10842行、1050 ~ 3098列共1536×2048的数据储存到文件CDdata2.mat中。

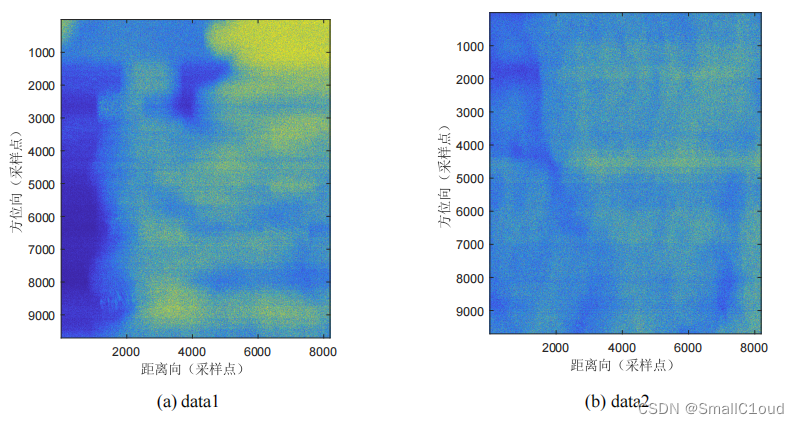
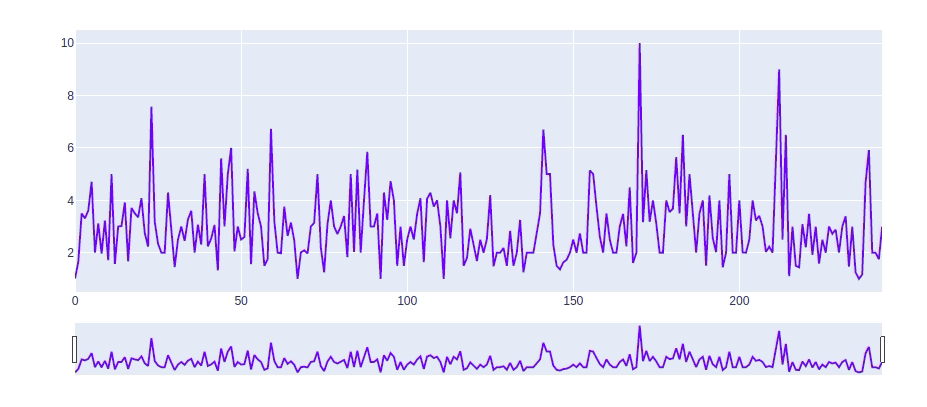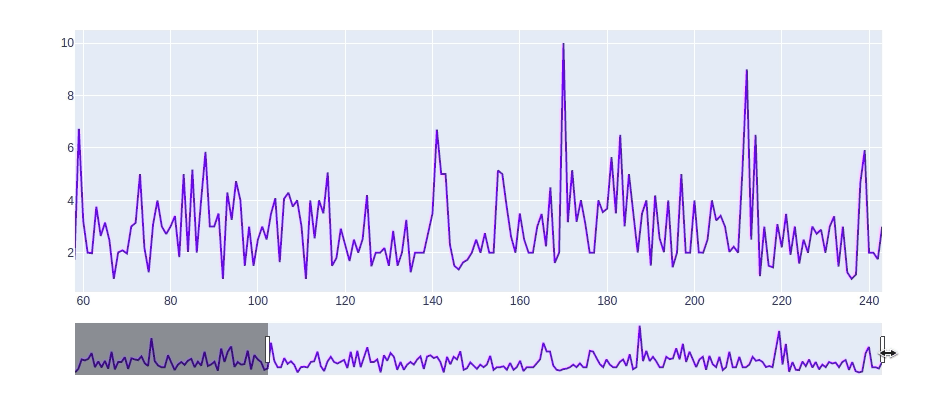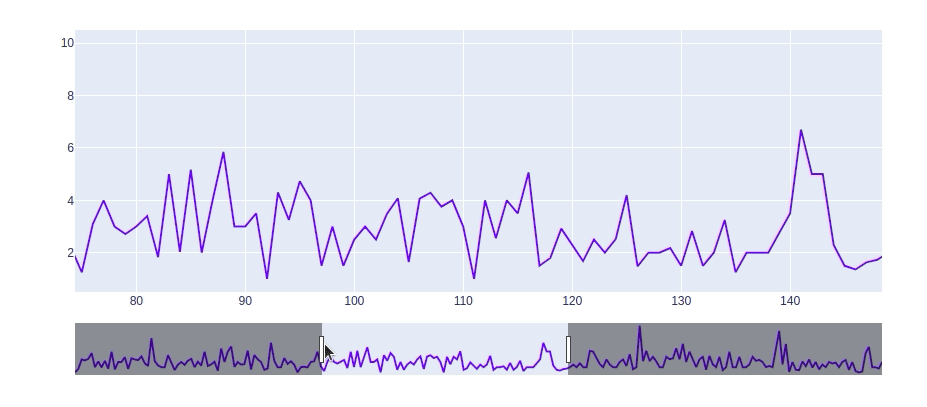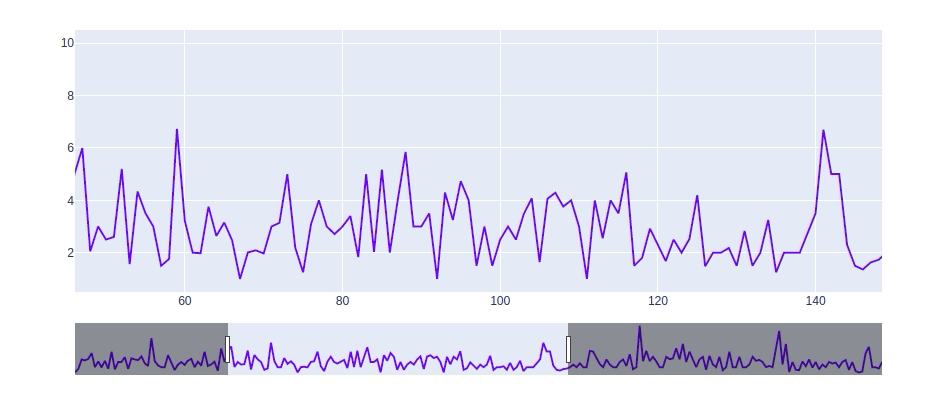
下图展示了未补零的原始数据

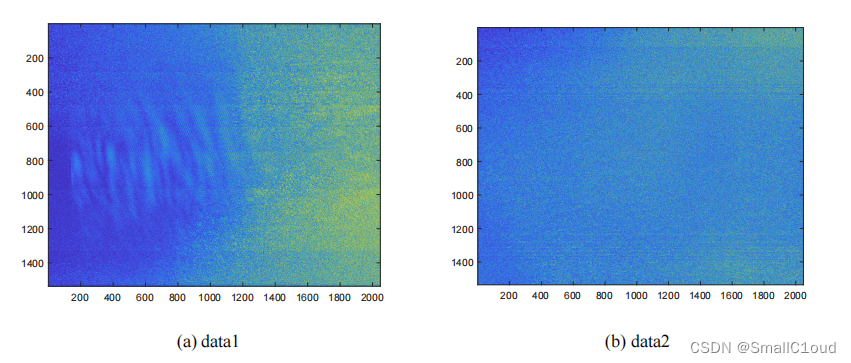
为解决成像反折问题。需要在时域进行补零，相当于延长了时间轴。下图给出了经RC、SRC和一致RCMC操作后的信号幅度图像，可以看出，在距离多普勒域，数据已被拉直。

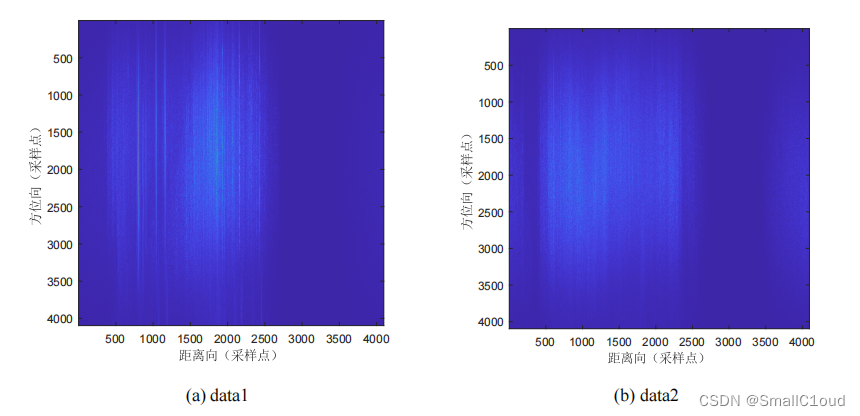
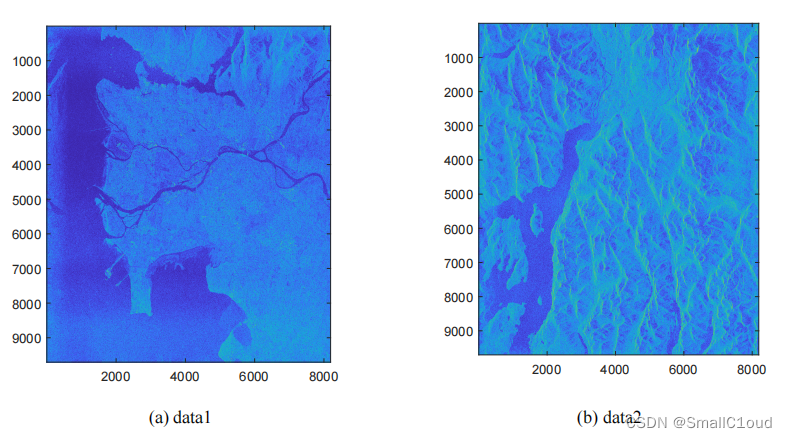
下图给出了CSA成像结果

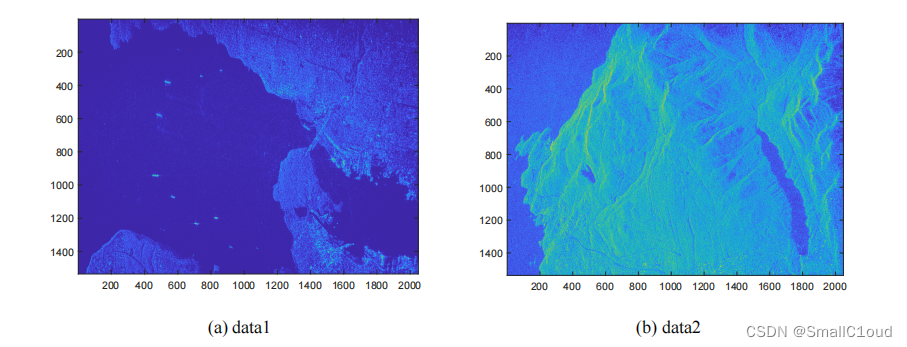
从（a）中可以清晰地看到海面上航行有六艘轮船。

9704×8192

从文件DAT_01.001中提取了1 ~ 9704行、1 ~ 8192列共9704×8192的数据储存到了CDdata1_9704 _ 8192.mat文件中；9705_19408行、1~8192列共9704×8192的数据储存到了CDdata2_9704_8192.mat文件中。

原始数据