代码随想录刷题题Day2

刷题的第二天，希望自己能够不断坚持下去，迎来蜕变。😀😀😀
刷题语言：C++ / Python
Day2 任务
977.有序数组的平方
209.长度最小的子数组
59.螺旋矩阵 II

1 有序数组的平方（重点：双指针思想）

在这里插入图片描述

1.1 暴力

思路：将数组里面所有元素平方，再排序。
时间复杂度： $O (n + n l o g n)$
C++:

class Solution {
public:vector<int> sortedSquares(vector<int>& nums) {for (int i = 0; i < nums.size(); i++){nums[i] *= nums[i];}sort(nums.begin(), nums.end());return nums;}
};

Python:

class Solution(object):def sortedSquares(self, nums):for i in range(len(nums)):nums[i] *= nums[i]nums.sort()return nums

1.2 双指针（非常重要的思想）

在这里插入图片描述
非递减顺序排序的整数数组 nums，返回每个数字的平方组成的新数组，要求也按 非递减顺序 排序
数组里面的元素平方之后，元素趋势如下图所示

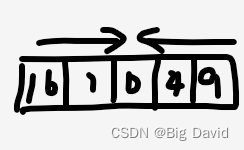
数组平方的最大值就在数组的两端，考虑双指针，i指向起始位置，j指向终止位置
伪代码：

vector<int> result;
k = nums.size - 1;
for(i = 0, j = nums.size-1;i<=j;) # i <= j，因为最后要处理两个元素if(nums[i]*nums[i]>nums[j]*nums[j])result[k--] = nums[i]*nums[i]i++elseresult[k--] = nums[j]*nums[j]j--
return result

时间复杂度： $O (n)$
C++:

class Solution {
public:vector<int> sortedSquares(vector<int>& nums) {int k = nums.size() - 1;vector<int> result(nums.size(), 0);for (int i = 0, j = nums.size() - 1; i <= j; ){if (nums[i] * nums[i] > nums[j] * nums[j]){result[k--] = nums[i] * nums[i];i++;}else{result[k--] = nums[j] * nums[j];j--;}}return result;}
};

Python:

class Solution(object):def sortedSquares(self, nums):i,j,k = 0, len(nums) - 1, len(nums) - 1res = [float('inf')] * len(nums)while i <= j:if nums[i] ** 2 > nums[j] ** 2:res[k] = nums[i] ** 2i += 1else:res[k] = nums[j] ** 2j -= 1k -= 1return res

2 长度最小的子数组 - （滑动窗口）

在这里插入图片描述

2.1 暴力解法

两个for循环，不断寻找符合条件的子序列
更新起始位置，终止位置每次都是一直往后遍历
时间复杂度： $O(n^2)$
C++:

class Solution {
public:int minSubArrayLen(int target, vector<int>& nums) {int res = INT32_MAX;// 2147483647int sum = 0;// 子序列数值之和int subLength = 0;// 子序列的长度for (int i = 0; i < nums.size(); i++) // 起点i{sum = 0;for (int j = i; j < nums.size(); j++) // 终止位置j{sum += nums[j];if (sum >= target) // 子序列和超过了s，更新result{subLength = j - i + 1; // 子序列的长度res = res < subLength ? res : subLength;break;}}}return res == INT32_MAX ? 0 : res;}
};

2.2 滑动窗口解法

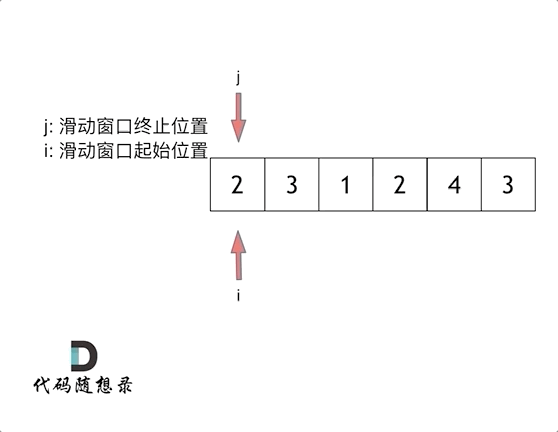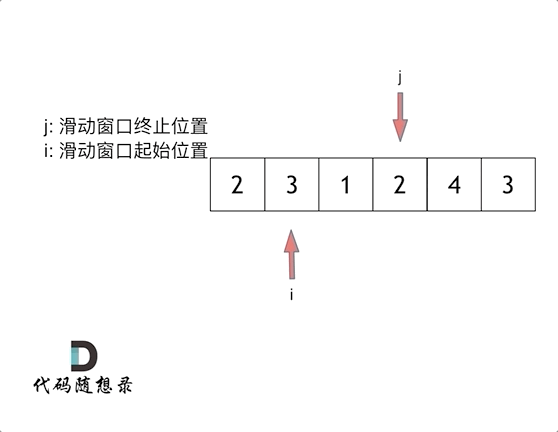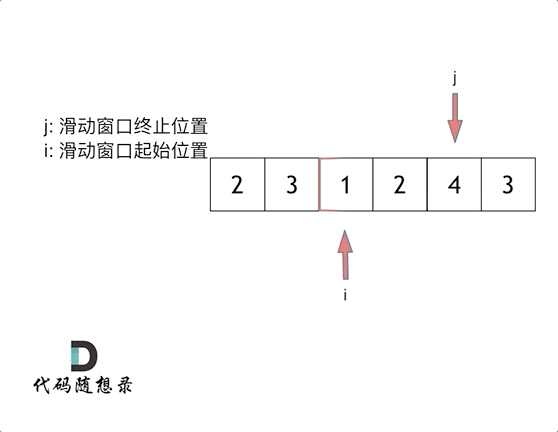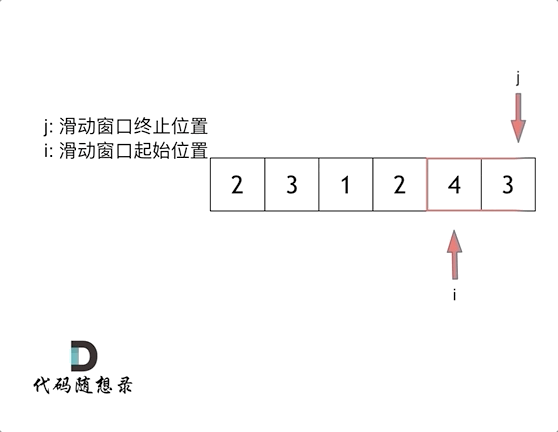
在这里插入图片描述

时间复杂度 $O (n)$
滑动窗口：不断的调节子序列的起始位置和终止位置，得出想要的结果
用一个for循环来做2个for循环所做的事情

索引下标j表示的是滑动窗口里面的终止位置
假设是起始位置，for循环一次一次往后移动，这个终止位置要把后面所有的元素都遍历一遍，这种就和暴力解法没有区别。
因此，这个for循环里面的j一定指向的是终止位置，而起始位置需要用动态移动（滑动窗口的精髓）的策略来移动起始位置。

解题关键：移动窗口的起始位置
终止位置随着for循环一个一个向后移动，集合里的元素之和sum>=target时，说明这个集合满足条件，收集这个集合的长度，起始位置就可以移动了。
就是当我们发现集合里面所有的元素和 >= target，我们再去移动起始位置，这样就实现了动态调整起始位置，来去收集不同长度区间里面的和

❗应该写if(sum >= target)还是 while(sum >= target)？
输入：target = 100, nums = [1,1,1,1,1,100]
如果是if，那么会漏掉其他情况

C++:

class Solution {
public:int minSubArrayLen(int target, vector<int>& nums) {int res = INT32_MAX; // 2147483647int i = 0; // 起始位置int sum = 0; // 子序列的和int subLength = 0; // 子序列的长度for (int j = 0; j < nums.size(); j++) // 更新终止位置{sum += nums[j];while (sum >= target) // 动态移动起始位置{subLength = j - i + 1; // 子序列的长度res = res < subLength ? res : subLength; // 记录较小的长度sum -= nums[i++]; // 移动起始位置i+1}}return res == INT32_MAX ? 0 : res; // 如果等于INT32_MAX，说明没有找到满足条件的子序列}
};

时间复杂度是O(n)
for循环里放一个while就认为是 $O(n^2)$ 是错误的，主要是看每一个元素被操作的次数，每个元素在滑动窗口后进来操作一次，出去操作一次，每个元素都是被操作两次，所以时间复杂度是 $O (2 n)$ ，也就是 $O (n)$

Python:

class Solution(object):def minSubArrayLen(self, target, nums):""":type target: int:type nums: List[int]:rtype: int"""l = len(nums)res = float('inf')i = 0 # 起始位置subLength = 0 # 子序列的长度cur_sum = 0 # 子序列和j = 0 # 终止位置while j < l:cur_sum += nums[j]while cur_sum >= target:subLength = j - i + 1res = min(res, subLength)cur_sum -= nums[i]i += 1j += 1return res if res != float('inf') else 0

3 螺旋矩阵

在这里插入图片描述
本题的求解依然要坚持循环不变量原则
坚持每条边左闭右开的原则

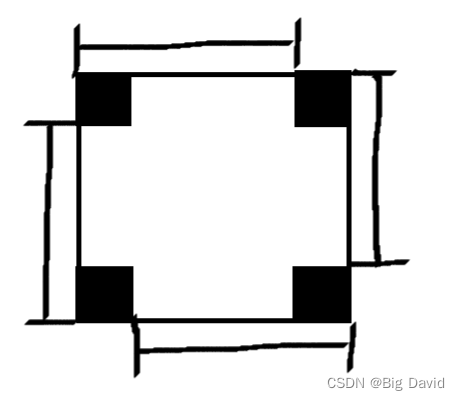
伪代码：

startx = 0;
starty = 0;
offset = 1; # 控制终止位置
count = 1;
while(n/2)
{i = startx;j = starty;for (j = starty; j < n - offset; j++){nums[startx][j] = count++;}for (i = startx; i < n - offset;i++){nums[i][j] = count++;}for (; j > starty; j--){nums[i][j] = count++;}for (; i > startx; i--){nums[i][j] = count++;}startx++;starty++;offset++;
}
if (n % 2)
{nums[n/2][n/2] = count;
}
return nums

C++:

class Solution {
public:vector<vector<int>> generateMatrix(int n) {vector<vector<int>> nums(n, vector<int> (n ,0); // 定义二维数组int i,j;int startx = 0; // // 定义每循环一个圈的起始位置int starty = 0;int offset = 1;   // 需要控制每一条边遍历的长度，每次循环右边界收缩一位int mid = n / 2;  // 矩阵的中间位置int loop = n / 2; // 循环次数int count = 1;while (loop--){i = startx;j = starty;// 填充上行从左到右（左闭右开）for (j = starty; j < n - offset; j++){nums[startx][j] = count++;}// 填充右列从上到下（左闭右开）for (i = startx; i < n - offset; i++){nums[i][j] = count++;}// 填充下行从右到左（左闭右开）for ( ; j > starty; j--){nums[i][j] = count++;}// 填充左列从下到上（左闭右开）for ( ; i > startx; i--){nums[i][j] = count++;}offset++;// 第二圈开始的时候，起始位置要各自加1startx++;starty++;}if (n % 2)// 如果n为奇数的话，需要单独给矩阵最中间的位置赋值{nums[mid][mid] = count;}return nums;}
};

Python:

class Solution(object):def generateMatrix(self, n):""":type n: int:rtype: List[List[int]]"""nums = [[0] * n for _ in range(n)]mid = n // 2  # 矩阵的中心点loop = n // 2 # 迭代次数# 起始点startx = 0starty = 0count = 1offset = 1    # 偏移量while loop:i = startxj = startywhile j < n - offset:nums[startx][j] = countcount += 1j += 1while i < n - offset:nums[i][j] = countcount += 1i += 1while j > starty:nums[i][j] = countcount += 1j -= 1while i > startx:nums[i][j] = countcount += 1i -= 1startx += 1starty += 1offset += 1loop -= 1if n % 2 != 0:nums[mid][mid] = countreturn nums