12.1平衡树（splay)，旋转操作及代码

平衡树

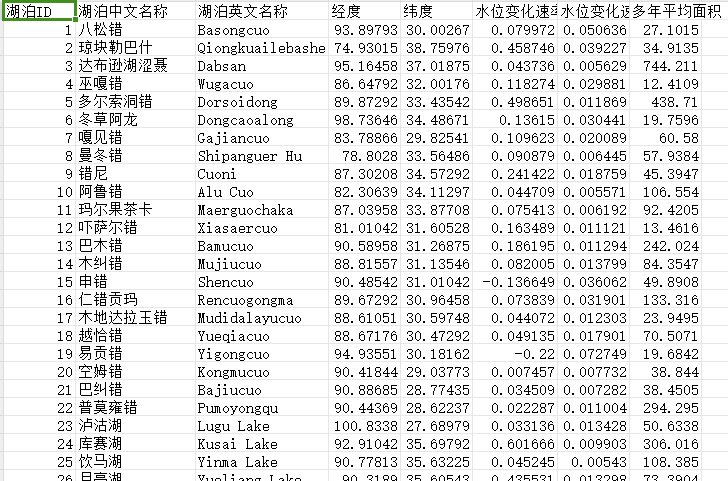
变量定义

tot表示结点数量，rt表示根的编号

v[i]表示结点i的权值

fa[i]表示结点i的父亲节点

chi[i][2]表示结点i的左右孩子

cnt[i]表示结点i的权值存在数量，如1123，v[3]=1，则cnt[3]=2;就是说i=3的三号结点的权值为1，那么三号结点的权值存在数量为2，即有两个1存在于数列当中，也就是说自变量是结点编号，因变量是结点的权值以及对应权值出现的次数

sz[i]表示结点i的子树中权值数量。sz[i]=sz[chi[i][0]]+sz[chi[i][1]]+cnt[i]

就是说i号结点存在的value的值的数量，chi[i][0]与chi[i][1]返回的是i号结点对应的两个孩子的编号，加起来就是左边的数量和右边的数量与根节点的数量和

操作

查询x的前驱：如果x有左子树，那么前驱是左子树里最靠右的结点；如果x没有左子树但有父亲结点，那么前驱是它左子树内最靠右的结点。

查询x的排名：如果x小于当前权值，则向左子树。答案加上左子树大小，如果x等于当前权值，将答案+1并返回；否则加上当前节点的cnt并向右子树

查询排名为k的数值：如果k小于左子树的大小，则向左子树

将k减去左子树大小，如果k<=0,则返回当前权值，否则向右子树

旋转

旋转操作的输入是原根节点，输出是新根结点

旋转的操作是对根节点而言的，就是说左旋是右孩子向左旋转上来；右旋是左孩子旋转上来

左旋就是右孩子成为根节点，然后原根节点成为新根结点的左孩子，新根结点的左孩子成为原根节点的最右侧孩子；右旋是左孩子成为新根节点，然后原根节点成为新根结点的右孩子，新根结点的右孩子成为

就右旋而言，要变的就两步，一步是让左孩子成为新根（也意味着左孩子失去原来的右孩子，原根节点失去原来的左孩子），另一步是让左孩子（新根）失去的右孩子接到原根（新根的右子树）的左侧

注意，由于原根失去左孩子（失去的左孩子成为了新根），所以原根在成为新根的右孩子节点时，是一定没有左孩子的，所以不用担心接不上以及接的位置，原根的左孩子的右孩子是一定可以接到原根的左孩子上的

原根A,原根左孩子B，原根左孩子的右孩子C，

用一个指针，定义为A的左孩子（即B），即表示右旋后的新的新根结点B。然后让A的左孩子为新根结点B的右孩子C（此时B还没发生改变），之后A就发生了变化，即左孩子不再是B而是C，然后再用新根指针，使B的右孩子为A

就是说在这一过程中，用了两个指针，一个指针为原根结点（输入），一个指针为新根结点（输出）

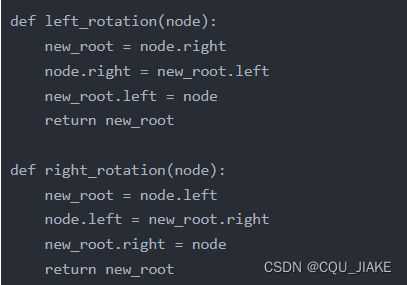
class TreeNode:def __init__(self, val):self.val = valself.left = Noneself.right = Nonedef left_rotation(node):new_root = node.rightnode.right = new_root.leftnew_root.left = nodereturn new_rootdef right_rotation(node):new_root = node.leftnode.left = new_root.rightnew_root.right = nodereturn new_root

左旋：

旋转操作是平衡二叉树中常用的操作，用于调整树的结构以保持平衡性。平衡二叉树的旋转操作包括左旋、右旋、左右旋和右左旋。

1. 左旋（Left Rotation）：对于一个节点，将其右子节点变为新的根节点，原根节点成为新根节点的左子节点，原右子节点的左子节点成为原根节点的右子节点。这个操作用于解决在插入或删除某个节点导致右子树过高的情况。

2. 右旋（Right Rotation）：对于一个节点，将其左子节点变为新的根节点，原根节点成为新根节点的右子节点，原左子节点的右子节点成为原根节点的左子节点。这个操作用于解决在插入或删除某个节点导致左子树过高的情况。

3. 左右旋（Left-Right Rotation）：先对节点的左子节点进行左旋，然后再对节点自身进行右旋。这个操作用于解决在插入或删除某个节点导致左子树过高，且其左子节点的右子树过高的情况。

4. 右左旋（Right-Left Rotation）：先对节点的右子节点进行右旋，然后再对节点自身进行左旋。这个操作用于解决在插入或删除某个节点导致右子树过高，且其右子节点的左子树过高的情况。

通过这些旋转操作，可以调整树的结构并保持树的平衡性。旋转操作的实质是通过节点之间的连接关系进行调整，从而改变树的形态。在实际应用中，旋转操作通常会涉及到节点的左右子树的高度计算、节点指针的重连等步骤。

需要注意的是，旋转操作只能保持局部的平衡性，有时可能需要多次旋转来达到整体的平衡。另外，旋转操作可能会改变树中节点的相对顺序，因此在进行旋转操作时需要注意维护节点的排序和二叉搜索树的性质。

struct Node
{int ch[2];int val;int ff;
}t[MAX];

ch是左右孩子。ff是记录这个结点的父节点

inline void rotate(int x)
{int y=t[x].ff;int z=t[y].ff;int k=(x==t[y].ch[1]);t[z].ch[y==t[z].ch[1]]=x;t[x].ff=z;t[y].ch[k]=t[x].ch[k^1];t[t[x].ch[k^1]].ff=y;t[x].ch[k^1]=y;t[y].ff=x;
}

输入是x，表示要旋转的结点的编号。通过y记录x的父节点，就是说y是x的父节点；z是y的父节点，是x的爷爷结点

k是表示结点x是其父结点的什么孩子。t[y].ch[1]返回的是y号结点的右孩子编号。如果是右孩子,则判断出来是1.不然则判断出来是0，就是说是左孩子就返回0，是右孩子就返回1

对于旋转的操作，就是利用了两个指针，借助了爷爷结点，即把x接到了爷爷结点上，然后就是确定接到爷爷结点的哪个孩子结点上。

具体步骤是先让爷爷节点的孩子结点设置为x,这时会断掉z与y的联系，z与x联系上；

然后让x的父节点设置为z，这时会断掉x与y的联系，x与z联系上。此时，y的孩子结点上记录的依然是x

然后让y的孩子结点变为x的孩子结点，让x的孩子结点的父节点变为y结点

最后让x的孩子结点设置为y，把y的父节点设置为x