一、回归的细分
机器学习中的回归问题是一种用于预测连续型输出变量的任务。回归问题的类型和特点如下:
- 线性回归(Linear Regression):线性回归是回归问题中最简单的一种方法。它假设自变量与因变量之间存在线性关系,并通过最小化预测值与真实值之间的差距来拟合最优直线。线性回归易于解释和实现,但对于非线性关系的建模能力有限。
-
多项式回归(Polynomial Regression):多项式回归是在线性回归的基础上引入多项式特征的一种方法。通过添加高次项来拟合更复杂的数据模式,可以更好地适应非线性关系。然而,多项式回归容易出现过拟合问题。
-
岭回归(Ridge Regression):岭回归是一种正则化线性回归方法,通过引入L2正则化项来控制模型的复杂度,防止过拟合。岭回归在特征之间存在共线性(即高度相关)时表现较好。【其核心思想是在最小化残差平方和的同时,加上一个惩罚项,该惩罚项与模型的参数大小有关。这个惩罚项可以将参数的估计值向零进行偏移,从而减少参数估计的方差。具体而言,岭回归使用L2范数作为惩罚项,即将参数的平方和添加到残差平方和中。】
-
Lasso回归(Lasso Regression):Lasso回归是另一种正则化线性回归方法,通过引入L1正则化项来促使模型具有稀疏性,即自动选择对预测目标更重要的特征。Lasso回归可以用于特征选择和降维。
-
弹性网回归(Elastic Net Regression):弹性网回归是岭回归和Lasso回归的结合,既具有L1正则化项的稀疏性特征选择能力,又具有L2正则化项的共线性处理能力。
-
支持向量回归(Support Vector Regression,SVR):支持向量回归是一种非常灵活的回归方法,通过引入核函数将输入空间映射到高维特征空间,从而实现非线性回归。SVR通过定义一个边界带,尽量使观测值落在该带内,同时最小化预测误差。【它基于支持向量机(Support Vector Machine,SVM)的思想,将分类问题扩展到回归问题上。
与传统的回归方法不同,SVR的目标是找到一个边界,使得样本点尽可能地落在该边界内,并且最大化落在边界上的样本之间的间隔。SVR通过引入一个容忍度范围(ε-tube)来容忍落在边界附近的样本点,即允许一部分样本点的预测误差落在容忍度范围内。因此,SVR旨在构建一个能够良好拟合数据并具有较小预测误差的超平面。
SVR的核心思想是通过寻找支持向量来建立回归模型。支持向量是指那些离边界最近的样本点,它们对于构建回归模型具有重要的作用。SVR的目标是找到一个最小化经验风险和模型复杂度的平衡点,从而获得一个效果良好且具有较好泛化能力的回归模型。
SVR可以使用不同的核函数来处理线性和非线性回归问题。常用的核函数包括线性核函数、多项式核函数和高斯径向基核函数等。这些核函数可以将原始样本映射到高维空间,从而使得原本线性不可分的问题在高维空间中变得线性可分。
SVR具有以下特点:SVR可以处理非线性回归问题,并具有较好的泛化能力。SVR通过引入容忍度范围(ε-tube)来允许一定的预测误差,增强了模型对噪声的鲁棒性。
总之,支持向量回归是一种用于解决回归问题的机器学习方法,通过寻找支持向量和引入容忍度范围来建立回归模型,能够处理非线性问题并具有较好的泛化能力。SVR的模型复杂度受支持向量数量的影响,通过选择合适的核函数和正则化参数,可以控制模型的复杂度,避免过拟合。SVR适用于小样本和高维数据的回归问题,具有较好的稳定性和性能。】
【当你无法在平面解决问题,你就要试图提升到空间维度解决问题】
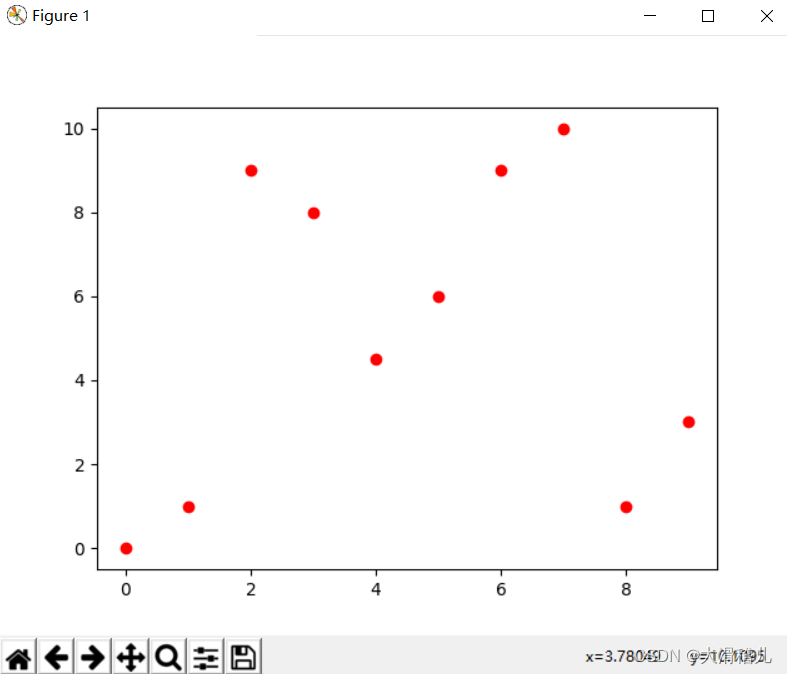
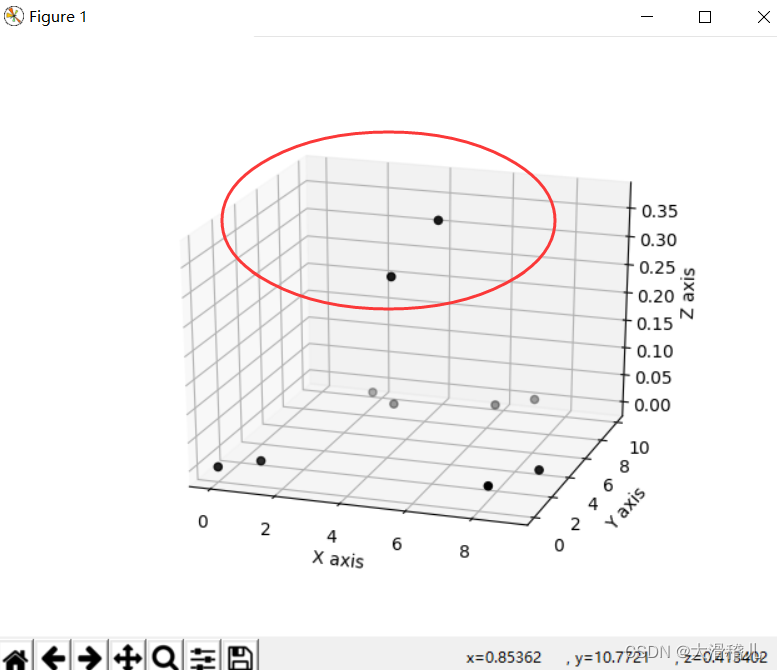
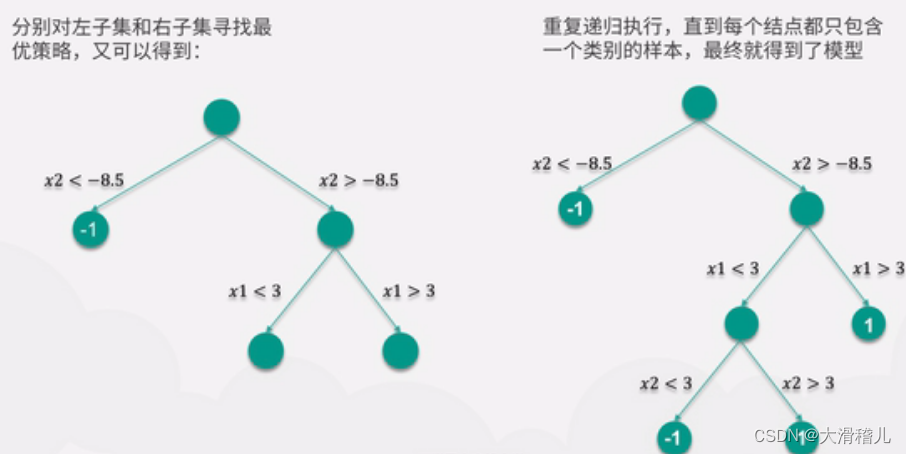
7.决策树回归(Decision Tree Regression):决策树回归使用树结构来建模数据,每个节点代表一个特征变量,每个分叉代表一个判断条件,每个叶节点代表一个输出值。决策树回归具有很好的解释性和非线性建模能力,但容易过拟合。
8.随机森林回归(Random Forest Regression):随机森林回归是基于决策树的集成学习方法,通过构建多个决策树并取其平均或投票来进行回归预测。随机森林回归具有较好的鲁棒性和泛化能力,能够处理高维数据和特征选择。【随机森林选取】
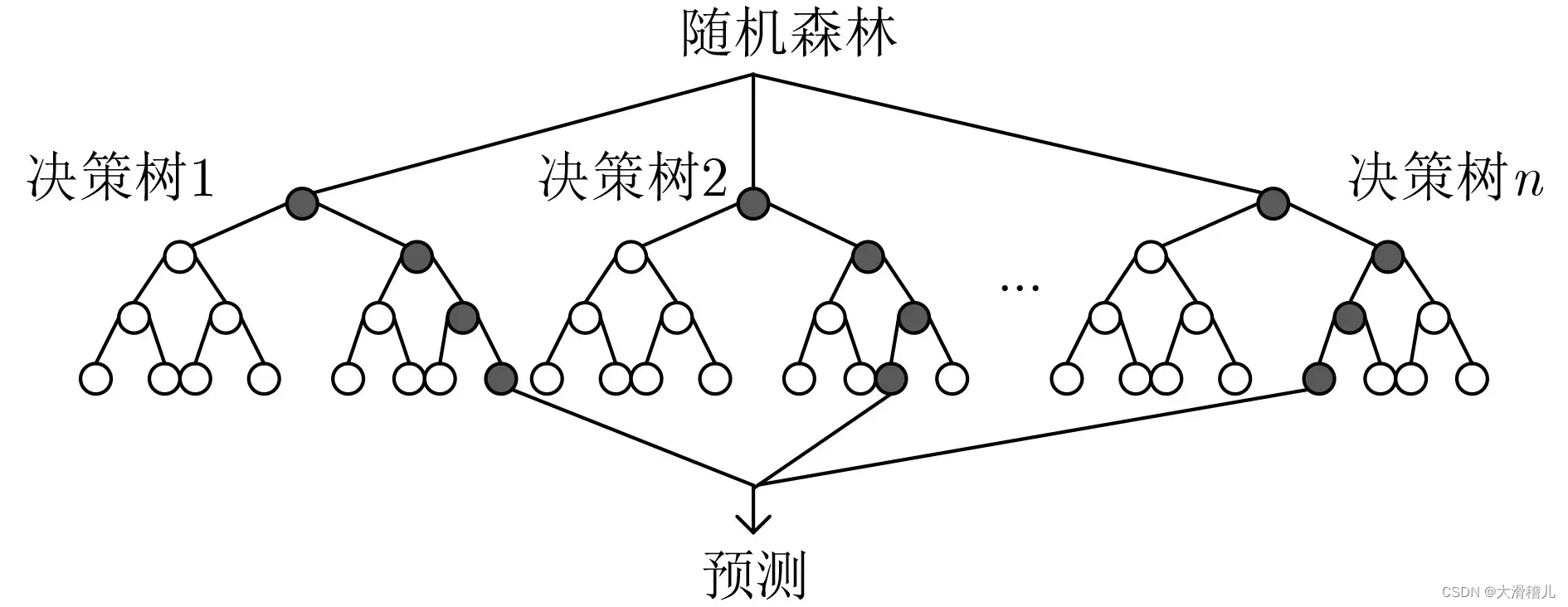
随机森林回归是一种集成学习算法,用于解决回归问题。它结合了决策树和随机性的特点,能够应对高维数据和复杂关系的建模。
随机森林回归的主要步骤如下:
①数据准备:将数据集划分为训练集和测试集,确保数据的质量和完整性。
②随机抽取自助采样集:从训练集中随机有放回地抽取一部分样本,形成一个新的子训练集,样本数与原训练集相同。
③随机选择特征子集:从所有特征中随机选择一部分特征,形成一个新的子特征集。
④构建决策树:使用子训练集和子特征集构建决策树模型。在构建过程中,采用递归的方式选择最佳的划分特征和划分点,直到满足终止条件(如节点中样本数小于某个阈值或达到最大深度)。
④构建多棵决策树:重复步骤2和步骤3,构建多棵决策树形成随机森林。
⑤预测:使用测试集数据,在每棵决策树上进行预测,并取平均值或投票得到最终的预测结果。
随机森林回归具有以下优点:
随机性能够降低过拟合的风险,提高模型的泛化能力。
能够处理高维数据和复杂关系,对异常值和缺失值具有较好的鲁棒性。
能够评估特征的重要性,用于特征选择和特征工程。
相对于单个决策树,随机森林可以更准确地进行预测。
需要注意的是,随机森林回归也有一些限制:
对于具有大量特征和少量样本的问题,可能存在过拟合的情况。
随机森林构建过程中需要消耗较多的计算资源和时间。
随机森林的模型可解释性相对较弱。
9.梯度提升回归(Gradient Boosting Regression):梯度提升回归是一种迭代的集成方法,通过逐步改善残差来拟合模型,并组合多个弱回归器的预测结果。梯度提升回归在回归问题上表现出色,但对于大规模数据集和异常值敏感。
10.神经网络回归(Neural Network Regression):神经网络回归使用多层神经网络来进行回归预测,可以灵活地建模复杂的非线性关系。神经网络回归通常需要大量的数据和计算资源来训练,但可以获得较好的预测性能。
二、回归可以实现分类吗?
机器学习中的回归模型本质上是用于预测连续型输出变量的,而分类则是将样本划分到不同的离散类别中。虽然回归和分类是两个不同的任务,但有一些方法可以通过对回归结果进行适当处理来实现分类。
一种常见的方法是使用阈值(Threshold)来将回归输出转化为二元分类。例如,设定一个阈值,当回归输出大于该阈值时,将样本分类为一类;当回归输出小于等于该阈值时,将样本分类为另一类。这种方法简单直观,但需要合理选择阈值,且不能处理多类分类问题。
另一种方法是使用回归模型的输出概率来进行分类。例如,对于线性回归模型,可以使用逻辑函数(如sigmoid函数)将回归输出映射到[0,1]区间,表示概率。根据概率大小,将样本分配给具有最高概率的类别。这种方法通常被称为逻辑回归,虽然名字中带有"回归",但实际上是一种二元分类算法。
还有一些其他方法,如支持向量回归(SVR)可以通过设置不同的阈值来实现多类分类。随机森林回归和梯度提升回归等集成模型也可以在回归结果的基础上进行分类。这些方法在实践中往往能够拟合非线性的决策边界。
需要注意的是,尽管可以通过适当的处理实现分类,但这样的方法可能无法完全满足分类问题的要求。为了更好地解决分类问题,通常会使用专门设计的分类算法,如逻辑回归、支持向量机、决策树、随机森林和神经网络等。这些算法在设计上更加关注离散类别的划分,具有更好的分类性能。因此,在实际应用中,建议根据具体问题的特点选择适合的分类算法。