有个技巧，若想熟悉语言的写法，可以照着其它语言的题解，写目标语言的代码，比如有C/C++的题解，写Python的算法，这样同时可以对比两种语言，并熟悉Python代码中API的使用，并且可以增强代码的迁移能力，语言只是一种实现的工具，不被语言束缚也是一种自由。

1. 合并两个有序数组

题目链接：合并两个有序数组 - leetcode
题目描述：
给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2，另有两个整数 m 和 n ，分别表示 nums1 和 nums2 中的元素数目。
请你 合并 nums2 到 nums1 中，使合并后的数组同样按 非递减顺序 排列。
注意：最终，合并后数组不应由函数返回，而是存储在数组 nums1 中。为了应对这种情况，nums1 的初始长度为 m + n，其中前 m 个元素表示应合并的元素，后 n 个元素为 0 ，应忽略。nums2 的长度为 n 。

解题思路：
(1) 排序法。将nums2添加至nums1并排序，但这样的做法未利用到nums1与nums2非递减的特性，时间复杂度是排序的时间复杂度$O((m+n)lo{g}_2(m+n))$，空间复杂度认为是快排的空间复杂度$O(lo{g}_2(m+n))$
(2) 双指针法。新建一个数组sorted用来存储，然后将nums1指向新数组的内容，用双指针比较nums1和nums2各元素的大小，存储至sorted数组中

Python3

排序法

class Solution:def merge(self, nums1: List[int], m: int, nums2: List[int], n: int) -> None:"""Do not return anything, modify nums1 in-place instead."""nums1[m:] = nums2nums1.sort()

双指针法

class Solution:def merge(self, nums1: List[int], m: int, nums2: List[int], n: int) -> None:"""Do not return anything, modify nums1 in-place instead."""p1, p2 = 0,0index_bound1, index_bound2 = m-1,n-1 # 数组下标索引边界，这和长度有区别sorted = []while p1 <= index_bound1 or p2 <= index_bound2:# 1.若有某一数组下标出界，表明该数组已判断完成，应存另一数组的值if p1 > index_bound1:sorted.append(nums2[p2])p2 += 1elif p2 > index_bound2:sorted.append(nums1[p1])p1 += 1# 2.比较两数大小，存更小的，以确保是非递减序列elif (nums1[p1] <= nums2[p2]):sorted.append(nums1[p1])p1 += 1else:sorted.append(nums2[p2])p2 += 1nums1[:] = sorted

2. 移除元素

题目描述：
给你一个数组 nums 和一个值 val，你需要 原地 移除所有数值等于 val 的元素，并返回移除后数组的新长度。不要使用额外的数组空间，你必须仅使用 O(1) 额外空间并 原地 修改输入数组。元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。
题目归纳：
即要将数值中值等于val的元素全部移除，并且不能使用额外的数组空间

解题思路：
双指针法。left指针从数组起点向右，right指针从数组终点向左，若nums[left]与val相等，就不断的将nums[left]的值与nums[right]的值交换，保证数组在[0,left]的纯洁性。

Python3

class Solution:def removeElement(self, nums: List[int], val: int) -> int:left, right = 0, len(nums) - 1while left <= right:if(nums[left] == val): # swap,将等于val的放到数组后面去nums[left],nums[right] = nums[right],nums[left]right -= 1else:left += 1return left

3. 删除有序数组中的重复元素

题目描述：
给你一个 非严格递增排列 的数组 nums ，请你 原地 删除重复出现的元素，使每个元素 只出现一次 ，返回删除后数组的新长度。元素的 相对顺序 应该保持 一致 。然后返回 nums 中唯一元素的个数。
考虑 nums 的唯一元素的数量为 k ，你需要做以下事情确保你的题解可以被通过：
更改数组 nums ，使 nums 的前 k 个元素包含唯一元素，并按照它们最初在 nums 中出现的顺序排列。nums 的其余元素与 nums 的大小不重要。
返回 k 。
题目归纳：
首先分析该有序数组的特点
由于数组有序，且非严格递增
故对于任意 i < j，若有nums[i] = nums[j]
则有任意i <= k <= j，nums[i] = nums[k] = nums[j]
利用上述特点，使用快慢指针进行删除重复元素

解题思路：
快慢指针法。慢指针用来指向第一个(可能)遇到重复元素的位置处，而快指针寻找新元素，当快指针找到新元素，把新元素赋值给慢指针处做替换。

Python3

class Solution:def removeDuplicates(self, nums: List[int]) -> int:slow_p = 1 # 数组若只有一个元素，则下标为0, 这样的数组中不会有重复项for fast_p in range(1, len(nums), 1):if(nums[fast_p-1] != nums[fast_p]): # 快指针找到新元素，利用了任意i <= k <= j，nums[i] = nums[k] = nums[j]特性nums[slow_p] = nums[fast_p]slow_p += 1 # slow_p的增加是有条件的，要找到不相同的元素return slow_p

---

7. 买卖股票的最佳时机

题目链接：买卖股票的最佳时机 - leetcode
题目描述：
给定一个数组 prices ，它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。你只能选择 某一天 买入这只股票，并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润，返回 0 。
题目归纳：
先买后卖是常规操作，即做多。而先将股票卖出，后买入同样数量股票归还于他人，即做空，这道题目不考虑做空，考虑做空也简单，把股票价格数组反转一下，还是先买后卖，就变成“做空”了。这道题目等价于：给定数组，求数组中的两个数字间的最大差值。在实际中，相当于你只能买和卖各一次，减法只有一次，解这道题目，代入感不要太强，不要真的以为自己在买股票，然后傻乎乎的去一个个的从左到右遍历，并且假设自己不知道明天的股票价格，你是开了上帝之眼，知道整个股票价格数组的！用爬山类比：相当于只记录从山脚到山顶的高程差。

解题思路：
(1) 记录当前遇到的 min_price 即最低股价
(2) 记录 当前收益 = (当前股价 - 最低股价) ，与最大收益做比较并更新最大收益
(3) 返回最大收益

Python3

class Solution:def maxProfit(self, prices: List[int]) -> int:inf = int(1e9) # 10^9min_price = infmax_profit = 0 # 第一天收益为0for price in prices:max_profit = max(price - min_price, max_profit) # 这样可以求得全局的最大收益min_price = min(price, min_price)return max_profit

---

8. 买卖股票的最佳时机Ⅱ

题目链接：买卖股票的最佳时机Ⅱ - leetcode
题目描述：
给你一个整数数组 prices ，其中 prices[i] 表示某支股票第 i 天的价格。在每一天，你可以决定是否购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。你也可以先购买，然后在 同一天 出售。返回 你能获得的 最大 利润 。
题目归纳：
与上一题的区别：同一天也可以买和卖，并且可以在多天多次买卖，其它条件与前面那道题一致，只能有一只股票。也等价于：给定数组，可以多次求差值(只能后减前)，求数组中的最大 差值总和。用爬山类比：相当于记录从山脚到山顶的高程差之和，即所有上坡高度之和。

解题思路：
(1) 若明天股价大于今天股价，可以卖出。
(2) 只要有股价上涨，就可以卖出。

Python3

贪心法

class Solution:def maxProfit(self, prices: List[int]) -> int:# 贪心解法sum_profit = 0n = len(prices)print(prices[-1]) # 注意python中这样写是没有数组越界的警告的，而是数组的第size-1个元素for i in range(1, n): # (1,n)而不是(0,n)sum_profit += max(0, prices[i] - prices[i-1]) # 只要有股价上涨，就可以卖出。return sum_profit

动态规划法

这题的动态规划算法必须学会，这是解下一步的股票题的基础。

class Solution:def maxProfit(self, prices: List[int]) -> int:# 动态规划解法# 考虑一个数组dp# dp[i][0] 为，当天未持有股票，所获得的最大收益# dp[i][1] 为，当天  持有股票，所获得的最大收益# 那么可以列出转移方程：# dp[i][0] = max( dp[i-1][0], dp[i-1][1] + prices[i] ) # 之所以加上prices[i]，是因为今天要卖出这只股票，会获得prices[i]这么多的收益# 同理# dp[i][1] = max( dp[i-1][1], dp[i-1][0] - prices[i]) # 之所以减去prices[i]，是因为今天要买入这只股票，会损失prices[i]这么多的收益# 建立dp数组n = len(prices)rows = ncols = 2dp = [ [0 for _ in range(cols)]for _ in range(rows) ]# 赋初值dp[0][0] = 0dp[0][1] = -prices[0]for i in range(1, n):dp[i][0] = max( dp[i-1][0], dp[i-1][1] + prices[i] )dp[i][1] = max( dp[i-1][1], dp[i-1][0] - prices[i] )# 最后一天不能拥有股票，因为还有股票的话肯定是利益受损的return dp[n-1][0]

---

11. H 指数

题目描述：
给你一个整数数组 citations ，其中 citations[i] 表示研究者的第 i 篇论文被引用的次数。计算并返回该研究者的 h 指数。
根据维基百科上 h 指数的定义：h 代表“高引用次数” ，一名科研人员的 h 指数是指，他（她）至少发表了 h 篇论文，并且每篇论文至少被引用了 h 次。如果该 h 有多种可能的值，h 指数是最大的那个。
题目归纳：
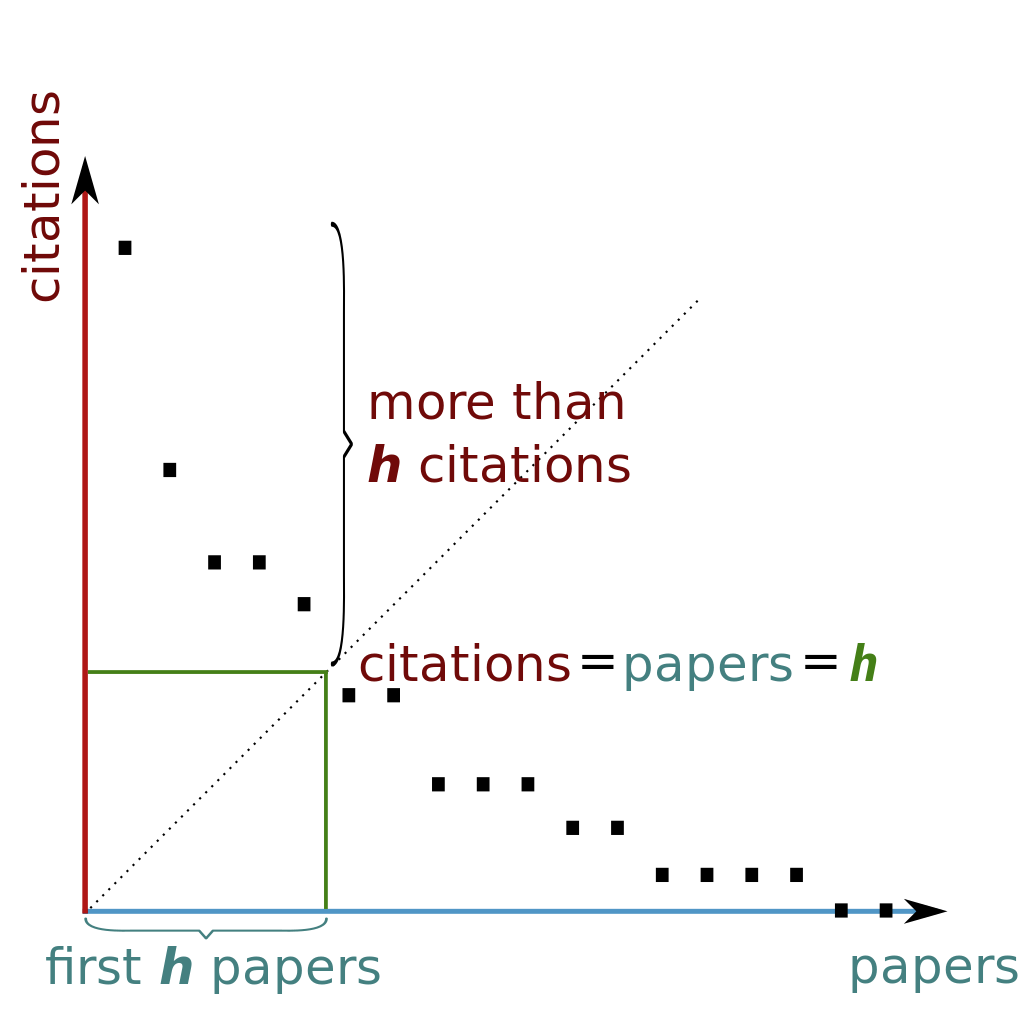
H-index Wiki，我想，h 指数的基本思想是：论文发的越多，不一定代表水平越高，而是发的越多，也要引用的越多才行，引用数认为是质，发表数认为是量，即有质有量 h 指数才高，可以看出原始的 h 指数有个缺点，如果论文发的少引用的多，h 指数也不会很高，也就是有质无量的 h 指数低，无质无量，无质有量自然就更低了，这里把两个量的量纲统一了，就得到了下面的图。

解题思路：
(1) 排序法。将数组citations从高到底排列，h不断增加，直到引用数 h 无法增大，则返回 h 。对应上图，就是寻找到虚线和数据分布的“分界点”，在papers(citations)坐标轴上的值。
(2) 计数排序法。

Python3

排序法

时间复杂度：$O(nlo{g}_{2}n)$，$n$为数组citations长度
空间复杂度：$O(lo{g}_{2}n)$，$n$为数组citations长度

class Solution:def hIndex(self, citations: List[int]) -> int:sorted_citation = sorted(citations, reverse = True)# python里可以用分号在一行中分割语句，曾经python为了阅读的简便性，抛弃了分号，现在又拿回来了，会不会有一天，这些语言来一个大一统，赋值号居然还有:=，=这两种写法，想出:=的人我很好奇他个人的精神状态h = 0; i = 0; n = len(citations)while i < n and sorted_citation[i] > h:h += 1i += 1return h

计数排序法

【排序算法】计数排序 - bilibili
计数排序是一种非比较排序，比较排序的复杂度下限是O(nlogn)已经得到过论文证明。

class Solution:def hIndex(self, citations: List[int]) -> int:# 新建并维护一个数组citation_papers，来记录当前引用次数的论文有多少篇# 对于论文i引用次数citations[i]超过论文发表数len(citations)的情况，将其按总论文发表数len(citations)计算即可，这样排序的数的大小范围就可以降低至[0,n=len(citations)]# 从而计数排序的时间复杂度，就降低至O(n)。现实中，一个学者一辈子能发表的论文数量顶天了也就百来篇，再夸张点，一千篇，不需要考虑n是无穷增长的，这点大小对计数排序是恰到好处的，因为计数排序就适合范围不大的排序。n = len(citations); H_papers = 0 # H_papers: 符合H指数的论文数citation_papers = [0] * (n+1) # 生成计数排序数组，用到了python的扩充操作，此数组下标为citation，数组内容为paper数量# 计算计数排序数组for c in citations:if c >= n:             # 引用次数超过论文发表数，引用次数按发表论文数计算citation_papers[n] += 1else:citation_papers[c] += 1# 倒序遍历for citation in range(n, -1, -1): # (-1, n] step = -1，实际上的下标范围即[0,n]H_papers += citation_papers[citation]if citation <= H_papers:return citationreturn 0

二分查找