L1Loss

nn.L1Loss 也称为平均绝对误差（Mean Absolute Error，MAE）。它计算预测值与真实值之间的差异（即误差），然后取绝对值并求和，最后除以样本数量得到平均误差。具体来说，对于一批大小为 $N$ 的样本，nn.L1Loss 的计算公式如下：

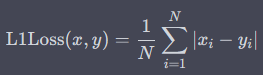
其中，$x$ 为模型的预测输出，$y$ 为样本的真实标签。

nn.L1Loss 通常用于回归问题中，例如预测房价、预测人的年龄等。它的优点是可以对异常值不敏感，即单个异常值不会对整体误差产生过大的影响。因此，它经常被用作回归问题的基准指标。

在 PyTorch 中，可以通过调用 nn.L1Loss() 函数来创建一个 L1 损失函数的实例。同时，它也可以作为一个组件被添加到神经网络模型中，用于反向传播计算梯度。

MSELoss

nn.MSELoss 也称为均方误差（Mean Squared Error，MSE）。它计算预测值与真实值之间的差异（即误差），然后取平方并求和，最后除以样本数量得到平均误差。具体来说，对于一批大小为 $N$ 的样本，nn.MSELoss 的计算公式如下：

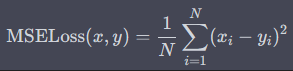
其中，$x$ 为模型的预测输出，$y$ 为样本的真实标签。

nn.MSELoss 也通常用于回归问题中，例如预测房价、预测人的年龄等。它的优点是对误差的大值敏感，因此可以使模型更加关注样本中误差较大的部分，从而提高模型的准确性。

在 PyTorch 中，可以通过调用 nn.MSELoss() 函数来创建一个 MSE 损失函数的实例。同时，它也可以作为一个组件被添加到神经网络模型中，用于反向传播计算梯度。

CrossEntropyLoss

nn.CrossEntropyLoss 用于多分类问题中。它的计算方式是将 Softmax 函数的输出和真实标签作为输入，然后计算它们的交叉熵损失（Cross-entropy Loss）。具体来说，对于一批大小为 $N$ 的样本，nn.CrossEntropyLoss 的计算公式如下：

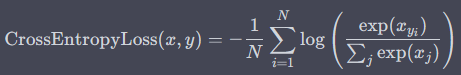
其中，$x$ 为模型的预测输出，$y$ 为样本的真实标签。

nn.CrossEntropyLoss 在内部自动进行 Softmax 计算，因此输入的 $x$ 不需要经过 Softmax 函数处理。在计算过程中，交叉熵损失越小，表示模型预测的结果和真实结果越接近，模型的性能也越好。

在 PyTorch 中，可以通过调用 nn.CrossEntropyLoss() 函数来创建一个交叉熵损失函数的实例。同时，它也可以作为一个组件被添加到神经网络模型中，用于反向传播计算梯度。

BCELoss

nn.BCELoss 也称为二元交叉熵损失（Binary Cross-Entropy Loss）。它的计算方式是将模型的预测输出和真实标签作为输入，然后计算它们之间的二元交叉熵损失。具体来说，对于一批大小为 $N$ 的样本，nn.BCELoss 的计算公式如下：

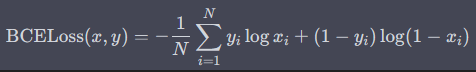
其中，$x$ 为模型的预测输出，$y$ 为样本的真实标签。该损失函数适用于二分类问题，其中每个样本只有两种可能的类别标签。对于多分类问题，通常使用 nn.CrossEntropyLoss。

nn.BCELoss 在内部自动进行 Sigmoid 计算，因此输入的 $x$ 不需要经过 Sigmoid 函数处理。在计算过程中，二元交叉熵损失越小，表示模型预测的结果和真实结果越接近，模型的性能也越好。

在 PyTorch 中，可以通过调用 nn.BCELoss() 函数来创建一个二元交叉熵损失函数的实例。同时，它也可以作为一个组件被添加到神经网络模型中，用于反向传播计算梯度。

参考

https://chat.openai.com/chat/