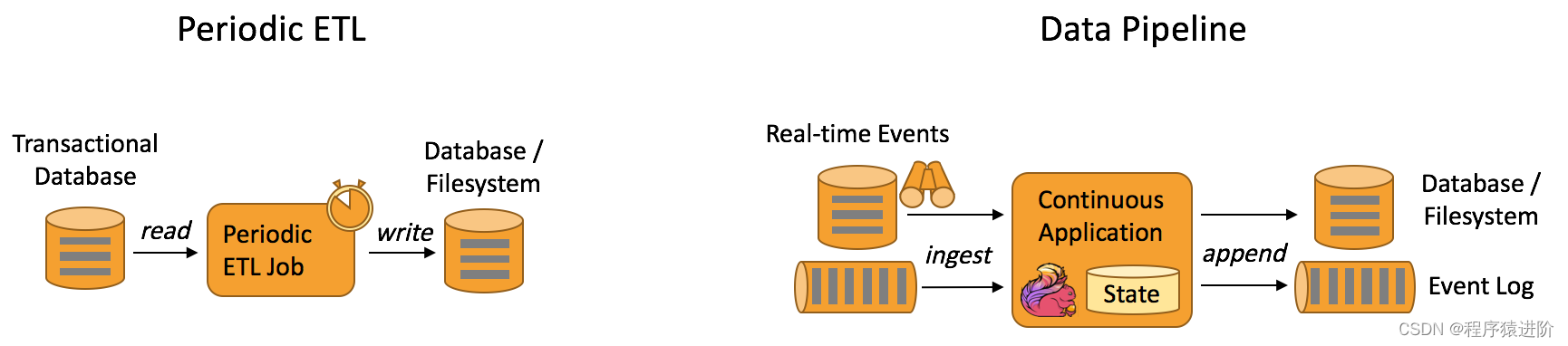
前言：

        这章节主要讲解常用的分类器原理.分类主要是要找到一个映射函数

          比如垃圾邮件分类 :

         c=0, 垃圾邮件  c=1 正常邮件

      主要应用场景： 垃圾邮件分类,手写数字识别,金融信用评估.

       这里面简单了解一下，很少用

目录：

    1： Generative model

    2:    高斯分类器

    3:    高斯分类器跟其它模型关系

---

一 Generative model

     朴素贝叶斯分类器：

     以二分类为例：

         不同类别

       : 不同类别出现的概率，先验概率

      : 条件概率,不同类别中出现x的概率

  模型

          (贝叶斯联合分布推导)

    例子：

    有两个盒子,里面分别放绿球和红球

       

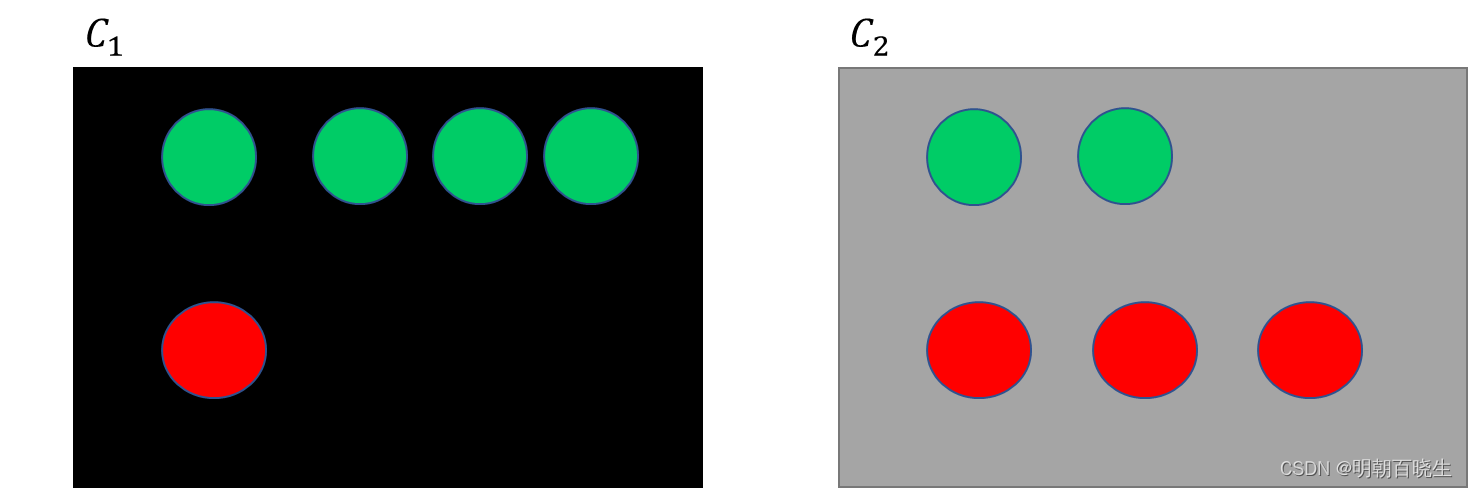
现在有个绿色的球,它来自哪个盒子

    

   其中

                 

     所以

      

      

---

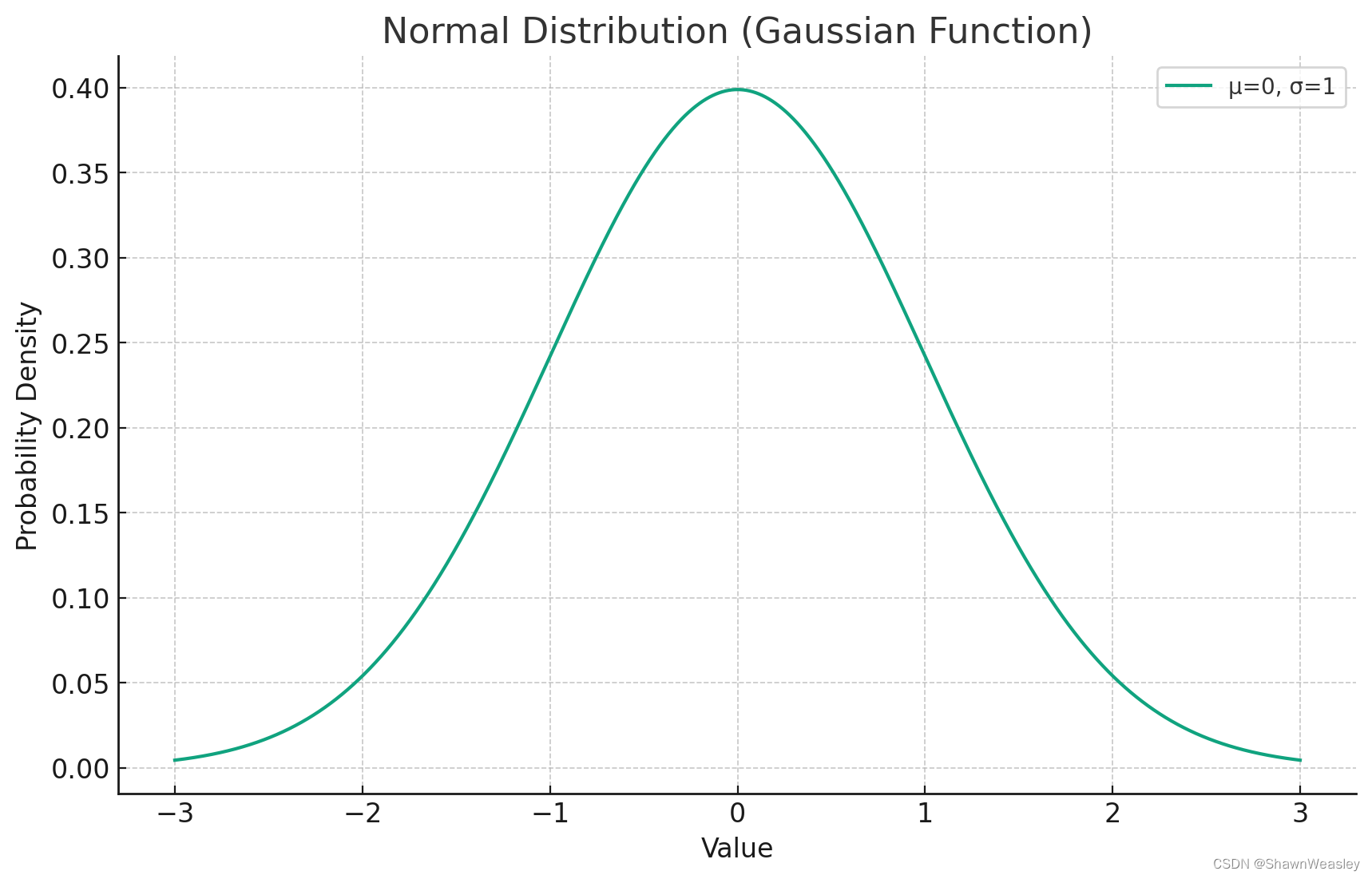
二  高斯分类器

     2.1  模型

        假设不同类别服从不同的高斯分布

        输入x ,输出 对该类别的概率

       

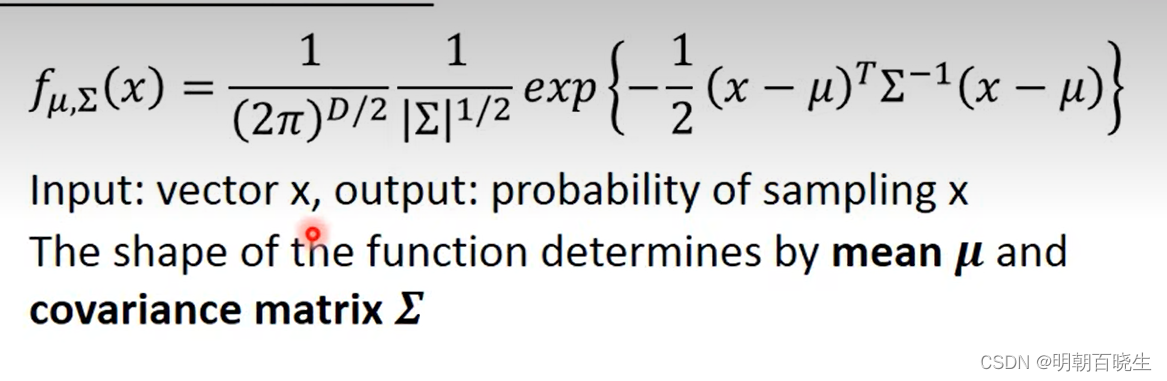
       u : 均值

        : 协方差矩阵  

     

a = np.cov(x,y)

   2.2  主要流程

             

       2.3 maximum likelihood 极大似然估计（计算u,）

                高斯分类器第一步要得到均值,和方差。均值,方差如何获取？

                我们通过极大似然估计 计算均值 和 协方差矩阵

               我们有训练样本 

                我们要找到使得下面概率最大

                 

                 这个值就是样本均值和样本的协方差，假设有79个点

              

            2.3 高斯分类器问题   

           不同均值,方差的高斯分类器容易发生过拟合.

           为了降低过拟合，通常假设不同类别的方差一样,均值不同. 通过增加样本数降低方差 。如下图两类样本.

---

三  高斯分类器跟其它模型关系

1： 跟Sigmoid 关系

     设   

     则

     

                   

                   

                   

 3.2  跟Linear 函数的关系

           

                 

  当  时候,可以进一步简化

   

非x 的项可以看作常数b

x项前面可以看作w

 z=wx+b