选自《洛谷深入浅出进阶篇》——欧拉函数+欧拉定理+扩展欧拉定理

欧拉函数：

欧拉函数定义： $\psi \left ( n \right ) =$ 1~n中与n互质的数的个数。比如 $\psi \left ( 12 \right ) = 4$
欧拉函数是积性函数：（也就是）当 n与m互质的时候： $\psi \left ( nm \right ) = \psi \left (n \right ) \psi \left(m \right )$
由算术基本定理，我们可以设n= $\prod_{i=1}^{m} p_{i}^{k_{i}}$ ，那么我们只要计算出 $\psi \left(p_{i}^{k_{i}} \right )$ 的取值就能求出 $\psi \left(n \right )$ 的取值。下面给出证明

$\psi \left(p_{i}^{k_{i}} \right )$ 的取值怎么求？也就是求1~ $p_{i}^{k_{i}}$ 中与 $p_{i}^{k_{i}}$ 互质的数的个数

我们可以求与 $p_{i}^{k_{i}}$ 不互质的数的个数，由于p是质数，所以与 $p_{i}^{k_{i}}$ 不互质的数一定是p的倍数

那么1~ $p_{i}^{k_{i}}$ 中，p的倍数就是 $\frac{p_{i}^{k_{i}}}{p}=p_{i}^{k_{i}-1}$ , 那么我们就知道与 $p_{i}^{k_{i}}$ 不互质的数的个数就是 $p_{i}^{k_{i}}-$ $p_{i}^{k_{i}-1 }$ 。也就是 $p_{i}^{k_{i}}\left(1-\frac{1}{p} \right )$

由于 $p_{i}^{k_{i}}$ 之间互质，且欧拉函数是一个积性函数，那么有

$\psi \left(n\right) = \prod_{i=1}^{m} \psi \left( p_{i}^{k_{i}} \right ) =\left(\prod_{i=1}^{m} p_{i}^{k_{i}} \right)\cdot \left(\prod_{i}^{m}\left(1-\frac{1}{p}\right)\right)=n\cdot \prod_{i}^{m}\left(1-\frac{1}{p} \right)$

所以我们只需要求出n的所有质因子p，然后求出 $1-\frac{1}{p}$ 的乘积即可

phi = n;
for(int i=2 ; i*i<=n ; i++ )if( n%i == 0 ){phi = phi/i * (i-1 )   // 1- 1/p == (p-1)/p 为了防止爆int，故意不写成phi*(i-1)/iwhile ( n%i==0 ) n/=i ;}
if(n!=1) phi =phi/n *(n-1);  //防止n有一个大于 sqrt（n）的质因子的情况

以上就是试除法求欧拉函数的板子，请牢牢记住，后面回经常用到。

下面介绍筛法求欧拉函数，可以以O（n）的时间来求2~n的欧拉函数。

const int N = 1e6 + 7;
int pri[N], phi[N], flag[N];
int tot;
int main() {phi[1]=1;for (int i = 2; i <= N; i++) {if (flag[i] == 0) {pri[tot++] = i;phi[i] = i - 1;}for (int j = 0; j < tot and pri[j] * i <= N; j++) {if (i % pri[j] == 0) {phi[i * pri[j]] = pri[j] * phi[i];flag[i * pri[j]] = 1;break;}else {flag[i * pri[j]] = 1;phi[i * pri[j]] = (pri[j] - 1) * pri[i];}}}
}

下面逐步分析这个板子：

首先我们需要写出一个线性筛的板子，然后根据欧拉函数的定义填充即可:

if (flag[i] == 0) {pri[tot++] = i;phi[i] = i - 1;}

这里很简单，当i是质数的时候，我们将i假如质数表，并且写上i的欧拉函数为i-1，phi[i]=i-1

for (int j = 0; j < tot and pri[j] * i <= N; j++) {if (i % pri[j] == 0) {phi[i * pri[j]] = pri[j] * phi[i];flag[i * pri[j]] = 1;break;}else {flag[i * pri[j]] = 1;phi[i * pri[j]] = (pri[j] - 1) * pri[i];}}

**这里依旧是欧拉筛的板子，对于任意一个合数，例如 i*pri【j】，**

**如果i和pri【j】互质的话，其欧拉函数为： phi【ipri【j】】=phi【pri【j】】 phi【i】；**

但是如果i和pri【j】不互质的话，我们就用上面写的表达式：

$\psi \left(n\right) = \prod_{i=1}^{m} \psi \left( p_{i}^{k_{i}} \right ) =\left(\prod_{i=1}^{m} p_{i}^{k_{i}} \right)\cdot \left(\prod_{i}^{m}\left(1-\frac{1}{p}\right)\right)=n\cdot \prod_{i}^{m}\left(1-\frac{1}{p} \right)$

**带入i*pri[j]可得：**

**$\psi\left(ipri[j] \right )=ipri[j]\prod_{i=1}^{n}\left( 1-\frac{1}{p}\right)=pri[j]*\psi(i)$**

至此，筛法求欧拉函数就结束了

欧拉定理：对于正整数a，n，若a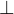 $\perp$ n，则 $a^{\psi\left(n\right)}\equiv 1 \left(mod \ n \right )$

扩展欧拉定理：

对于正整数a，n，始终有 $a^{\psi \left(n \right )}\equiv a^{k\psi \left(n \right )}\left(mod\ n \right ),k\epsilon N_{+}$

那么对于任意的正整数a，k，n ，当k大于 $\psi\left(n \right )$ 时，

$a^{k} \equiv a^{k\ mod \ \psi\left(n \right )+\psi\left(n \right )}\left(mod\ n \right )$

对于这些定理，此处不加以证明，背过即可。

下面给出一些例题，用来了解一些欧拉函数在算法竞赛中的应用

第一题：

《洛谷深入浅出进阶篇》p2568 GCD-CSDN博客https://blog.csdn.net/louisdlee/article/details/134886352?spm=1001.2014.3001.5502

第二题：

《洛谷深入浅出进阶篇》P5091 —— 扩展欧拉定理，快读取模。-CSDN博客https://blog.csdn.net/louisdlee/article/details/134891765?csdn_share_tail=%7B%22type%22%3A%22blog%22%2C%22rType%22%3A%22article%22%2C%22rId%22%3A%22134891765%22%2C%22source%22%3A%22louisdlee%22%7D

第三题：

《深入浅出进阶篇》p2303Longge ——欧拉函数的运用-CSDN博客https://blog.csdn.net/louisdlee/article/details/134892843?csdn_share_tail=%7B%22type%22%3A%22blog%22%2C%22rType%22%3A%22article%22%2C%22rId%22%3A%22134892843%22%2C%22source%22%3A%22louisdlee%22%7D

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.rhkb.cn/news/214015.html

如若内容造成侵权/违法违规/事实不符，请联系长河编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！